BVRIT College at Narsapur has a prayer room on campus where Muslim students can offer their prayers. They do not have to leave the campus for it.
Hope it helps !
Area - Definition, Area of Shapes Formula
Edited By Team Careers360 | Updated on Jul 02, 2025 05:32 PM IST
Area is the amount of space covered by a 2-D shape. The other way round, it is the quantity that measures the number of unit squares that cover the surface of a closed figure. For example, if we divide a figure in number of squares and then count those squares, it gives us the area for that shape. The standard unit of area is square units.
We have various shapes around us that have different shapes and sizes. Shapes can be found in various forms ranging from table as square, TV display as rectangle, bangle as circle, rubics cube as cube, a pipe as a cylinder, pizza slice as a triangle and much more. We come across them daily in some or the other way.
In this article we will dicuss about areas and perimeters of usual shapes that we come across our daily life such as triangle, rectangle, parallelogram, rhombus, cube, cuboid, etc. We will know about area of shapes, how do you find area and perimeter, area formulas, etc. We will look at the formulas for area and perimeter separately for every shape and also solve questions for a better understanding of the concept.
Area
Area is one of the fundamental concepts in geometry. Area is the amount of space covered within the shape. Technically, area measures the number of unit squares inside the given shape. Now, let us look into the formulas of area of shapes.
Triangle
A triangle is a three sided shape. There are three types of triangle. Namley, equilateral triangle, isoceles triangle and scalene triangle. Now let us look into the area of triangle.
Area of Triangle
Area of triangle is defined as the region covered by a triangle in an xy plane and is denoted as $A= \frac{1}{2} \times b \times h$ in general way, it applies to all types of triangle, be it scalene, isosceles, equilateral triangle. Units used are square units, like, $\mathrm{m}^2, \mathrm{~cm}^2$, in ${ }^2$, etc
Area of an Equilateral Triangle
From our previous knowledge we know that it is a triangle in which all the sides are equal. The perpendicular line that is drawn from the vertex of the triangle to the base divides the base into two equal parts as usual. Formula for area of equilateral triangle :
$A= \frac{(\sqrt{3})}{4} \times$ side $^2$
Area of an Isosceles Triangle
This type of triangle has two sides equal and the angles opposite to the equal sides are also equal. Formula for area of isosceles triangle used:
$A=\frac{1}{2} \times$ base $\times$ height
Rectangle
A rectangle is a four sided shape where opposite sides are equal and the diagonals are equal. The vertices of the rectangle makes $90^\circ$ with each other.
Area of Rectangle
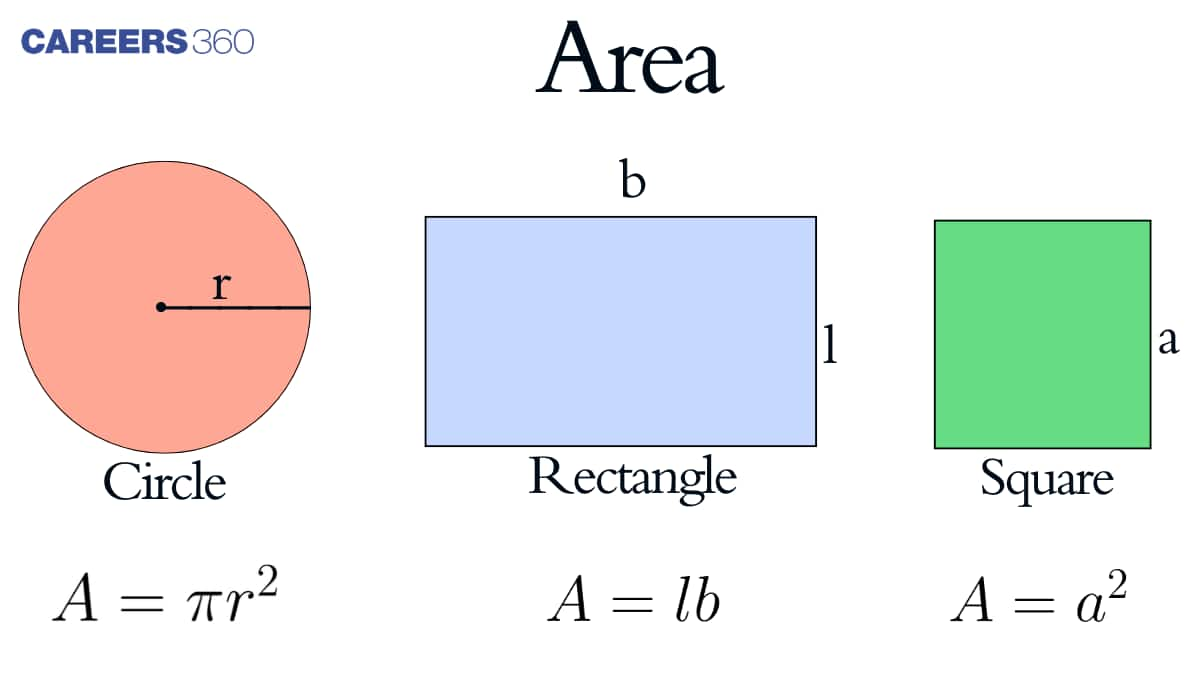
Area of rectangle means the space covered by a rectangle in a 2-D plane which can also be called as an xy plane covering 2 axis. A rectangle is a type of quadrilateral, a 2-D shape that has equal number of sides and vertices that is 4. All the four angles measure 90 degrees. The opposite sides are always equal and parallel to one other.
Area of Rectangle Formula
Area $=$ Length $\times$ Breadth
$
\mathrm{A}=\mathrm{lb}
$
How to Calculate the Area of Rectangle
We follow the below steps to find the area of rectangle:
Step 1: We write dimensions of length, width as given in the question to us.
Step 2: Next, we multiply length, width values.
Step 3: At last, we write answer in square units along with the calculated numeric value of area.
Circle
A circle is a round shape with no corners or edges.
Area of Circle
It is the space covered by the circle in an x-y plane. Or the other way around, the space occupied within the boundary/circumference of a circle.
Area of Circle Formula
We can find the area of circle once we know the diameter from which we find radius.
We use the following formulas:
- Area of circle $=\pi \times \mathrm{r}^2$, (r=radius)
- Area of circle in terms of diameter $=(\frac{\pi}{ 4}) \times \mathrm{d}^2,(\mathrm{~d}=$ diameter $)$
- Area of circle in terms of circumference $=\frac{C^2 }{4} \pi$, (C=circumference $)$
Square
A square is a four sided shape where all the sides are equal and the diagonals are equal. The vertices of the square makes $90^\circ$ with each other.
Area of Square
Generally, area of square is stated as the number of square units required to fill the shape. In other words, the area of a square is the region within its boundary. It can also be calculated with the help of other dimensions, for example the diagonal and the perimeter of the square.
Area of Square Formula
For finding area of square, we multiply the length of its two sides, which are always equal in measurement and so the unit of the area is given in square units.
Area of square $=$ Side $\times$ Side $=\mathrm{S}^2$
Area of square using diagonals $= \frac{Diagonal ^2}{ 2}$.
Trapezium
A trapezium is a four sided shape with two parallel sides and two non parallel sides.
Area of Trapezium
We know from previous knowledge that a trapezium is a quadrilateral, which is defined as a shape with four sides and one set of parallel sides. Area of a trapezium depends upon the length of parallel sides and height of the trapezium. It is measured in square units.
Area of Trapezium Formula
Formula used to find the area of trapezium:
Area $=(\frac{1}{2}) h(a+b)$
where,
- a and b are the length of parallel sides/bases of the trapezium
- h is the height or distance between parallel sides.
NEET Highest Scoring Chapters & Topics
This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.
Download E-bookHow to Calculate Area of Trapezium?
We take help from below mentioned steps to find area of trapezium:
- Step 1: First, we find the dimensions trapezium, that is., length of parallel sides and height.
- Step 2: Next we add the length of parallel sides.
- Step 3: Now we multiply the sum of parallel sides with the height of trapezium.
- Step 4: At last, we multiply the above value by $\frac{1}{2}$ to get the final result .
Parallelogram
A parallelogram is a four sided shape with parallel and equal opposite sides.
Area of Parallelogram
Area of parallelogram is the region covered by the parallelogram in a x-y plane. If we try to recall, a parallelogram is a special type of quadrilateral that has the pair of opposite sides as parallel. The opposite sides are always of equal length and opposite angles are of equal measures.
Area of Parallelogram Formula
To find the area of parallelogram, we simply multiply the base of the perpendicular by its height. These both quantities are always perpendicular to each other, whereas the lateral side of the parallelogram is not perpendicular to the base.
Hence,
Area $=\mathrm{b} \times \mathrm{h}$ Square units(b=base, h=height)
How to Calculate the Area of Parallelogram?
We calculate area of parallelogram by using its base and height. It can also be calculated if its two diagonals are known along with any of their intersecting angles or if the length of the parallel sides is known, along with any of the angles between the sides.
Area of Parallelogram Using Sides
Let us suppose p and q are the set of parallel sides of a parallelogram and h is the height, then based on the length of sides and height of it, formula for the area is :
Area $=$ Base $\times$ Height
$\mathrm{A}=\mathrm{p} \times \mathrm{h} \quad$ [sq.unit]
Area of Parallelogram Without Height
If the height of the parallelogram is unknown to us, then we use the concepts of trigonometry to achieve our aim.
Formula used :
Area $=a b \sin (x)$
Where a , b are the length of adjacent sides of the parallelogram and x is the angle between them.
Area of Parallelogram Using Diagonals
It can also be calculated using its diagonal lengths. There are two diagonals for a parallelogram, which always intersect each other. Suppose the diagonals intersect each other at an angle p, then the area of the parallelogram is given by:
Area $=\frac{1}{2} \times d_1 \times d_2 \sin (p)$
Rhombus
A rhombus is a four sided shape with parallel and equal sides.
Area of Rhombus
Area of Rhombus is defined as the amount of space covered by a rhombus in a two-dimensional space.It has four sides that are equal in length and are always congruent. It is also a type of a quadrilateral.
How to Calculate Area of Rhombus?
There exist three methods to find the area of a rhombus:
- Method 1: By using Diagonals
- Method 2: With the help of Base and Height
- Method 3: By using Trigonometry (using side and angle)
Area of Rhombus Using Diagonals: Method 1
We consider a rhombus ABCD, that has two diagonals, AC & BD.
Step 1: First we find the length of diagonal $1, d_1$. It is the distance between $A$ and $C$. The diagonals of a rhombus are perpendicular to each other.
Step 2: Next , we find the length of diagonal 2, $d_2$, the distance between $B$ and $D$.
Step 3: Then, we multiply both the diagonals, $d_1$, and $d_2$.
Step 4: Finally we divide the result by 2 and get answer.
Area of Rhombus Using Base and Height: Method 2
Step 1: We start by finding the base and height of the rhombus. The base of the rhombus is one of its sides, and the height is the altitude which is perpendicular distance from the chosen base to the opposite side.
Step 2: Then we multiply the base and the calculated height to get result.
Area of Rhombus Using Trigonometry: Method 3
We use this way when the side and one of its internal angles are given.
- Step 1: We square the length of any of the sides.
- Step 2: Next, we multiply it by Sine of one of the angles.
Cylinder
A cylinder is simply a three-dimensional structure having circular bases which are parallel to each other. It does not possess any vertices. It has 2 main values involved which are radius and its height.
Area of Cylinder
Area of cylinder is defined as the sum of the curved surface and the area of two circular bases.
The Surface Area of Cylinder = Curved Surface + Area of Circular bases
S.A. (in terms of $\pi)=2 \pi r(h+r)$ sq.unit
$\pi(\mathrm{Pi})=3.142$ or $=\frac{22}{7}$
$r=$ Radius
h = Height
Area of a Cylinder Formula
Surface Area of Cylinder: Surface area of cylinder is defined as the area of the curved surface of any cylinder having a base radius ‘r’, and height ‘h’, generally known as Lateral Surface Area (LSA). Formula for surface area of cylinder:
CSA or LSA $=2 \pi \times r \times h$ Square units
Base Area of Cylinder: It is a circular shape. Area of the circular bases of cylinder = $=2\left(\pi r^2\right)$
Total Surface Area of Cylinder: It is equal to the sum of the areas of all its faces. The total surface area with radius ‘r’, and height ‘h’ is equal to the sum of the curved area and circular areas of the cylinder.
TSA $=2 \pi \times r \times h+2 \pi r^2=2 \pi r(h+r)$ Square units
Sphere
It is a solid curved surface in such a way that every point on the surface is the same distance from the centre. We can say that it is a 3D representation of a circle and cover areas in all x,y,z planes in geometry. We can find it in various forms around us like celestial bodies, football, basketball, etc.
Area of Sphere
Area of Sphere is the region covered by a surface of a spherical object in a three-dimensional space. As we have discussed earlier, if we try to spin a circle around a fixed axis and visualize this in our mind, we will find that we obtain the figure of a sphere.
How to Find Area of Sphere?
Now to find the area of the sphere, we follow the steps:
- First we find the radius of the sphere.
- Then we mention the value of radius in the surface area formula, i.e. ($4πr^2$).
- After this we solve the expression and evaluate the final value.
Surface Area of Sphere
Surface area of sphere is the area occupied by the curved surface of the sphere. Circular shapes take the shape of a sphere when we observe them as three-dimensional structures. For example, a globe, cricket ball or a soccer ball.
Formula of Surface Area of Sphere
The formula for surface area of sphere just depends on the radius of the sphere.
Surface Area of Sphere $=4 \pi r^2 ; r=$ radius
In terms of diameter, $\mathrm{S}=4 \pi(\frac{\mathrm{d}}{2})^{2 ;}$ d=diameter
Cube
A cube is a 3 dimensional shape with equal sides. A cube is made up of 6 squares as their faces.
Surface Area of Cube
The definition of surface area of a cube states that if the total surface area is equal to the sum of all the areas of the faces of the cube. Since the cube has six faces, therefore, the total surface area of a cube will be equal to sum of all six faces of cube.
Surface Area of Cube Formula
Total Surface Area of Cube (TSA) Formula
TSA of the cube is obtained by multiplying the square of its side length by 6 . Thus, the formula becomes " $6 \mathrm{a}^2$ ".
Total Surface Area of a Cube $=\left(6 \times\right.$ side $\left.^2\right)$ square units
Lateral Surface Area of Cube (LSA) Formula
LSA of the cube is obtained by multiplying the square of its side length by 4 . Thus, the formula becomes " $4 \mathrm{a}^2$ ".
Lateral Surface Area of a Cube $=\left(4 \times\right.$ side $\left.^2\right)$ square units.
Solved Examples based on Areas
Example 1: Find the area of square with a side of 2 cm .
Solution: Area of a square $=$ side $\times$ side. Here, side $=2 \mathrm{~cm}$
Substituting the values in formula for area of square, we get $2 \times 2=4$.
The area of the square $=4$ square $\mathrm{cm} .$
Example 2: The dimensions of a rectangle are 10 cm and 8 cm . Find area of rectangle.
Solution: The area of a rectangle is the product of its length and width, which can be represented by the formula: Area $=1 \times \mathrm{w}$.
we get area of the rectangle $=10 \times 8=80 \mathrm{~cm}^2$
Example 3: Can you find the area of circle with a radius of 6 cm ?
Solution: The radius of the circle $=6 \mathrm{~cm}$
Area of a circle is calculated by the formula $\pi r^2$
Hence, area of circle $=\frac{22}{7} \times 6 \times 6=1113.04$ square cm .
Example 4: The length of rectangular field is 11 m and width is 5 m . Find the area of the rectangular field.
Solution: Given, Length $=11 \mathrm{~m}$
Width $=5 \mathrm{~m}$
Area of rectangle $=$ length $\times$ width $=11 \times 5=55$ sq.m.
Example 5: Find area of rectangle of $\mathrm{b}=2 \mathrm{~cm}$ and $\mathrm{h}=4 \mathrm{~cm}$.
Solution: Area of rectangle $=\frac{1}{2} \times b \times h=\frac{1}{2} \times 2 \times 4=4 \mathrm{sq} \mathrm{cm}$.
List of Topics Related to Area
| Area of Circle | Area of Isosceles Triangle |
| Area of Rectangle | Area of Sphere |
| Area of Parallelogram | Area of Quadrilateral |
| Area of Square | Area and Perimeter |
| Area of Equilateral Triangle | cm to inches converter |
Frequently Asked Questions (FAQs)
1. What is an area?
Area of a shape is a 2-D quantity that is measured in square units like square inches or $\left(\right.$ in $\left.^2\right)$, etc.
2. How do you find the area of irregular shapes?
The area of irregular shapes can be found by dividing the shape into unit squares. We can also approximate and find its value.
3. How do you prove the area of circle?
If a circle is folded into a triangle, the radius becomes the height of the triangle and the perimeter becomes its base which is $2 \times \pi \times r$. We know that the area of the triangle is found by multiplying its base and height and then dividing by 2 , which is: $\frac{1}{2} \times 2 \times \pi \times r \times r$. Therefore, the area of the circle is $\pi r^2$.
4. What is perimeter of triangle?
The total length of the boundary of a closed shape is called its perimeter. The perimeter of the triangle is the sum of three sides of the triangle.
5. What are the formulas for area and perimeter of square and rectangle?
The formulas for the area and perimeter of a square and a rectangle are as follows. Area of a square $=$ side $\times$ side. The perimeter of a square $=4 \times$ side. Area of a rectangle $=$ length $\times$ breadth. Perimeter of a rectangle $=2 \times$ (length + width )
6. What is the general formula for the area of a parallelogram?
The area of a parallelogram is calculated by multiplying its base (b) by its height (h): Area = b × h. The height must be perpendicular to the base, not the slanted side.
7. Why does the formula for a parallelogram's area work, even though it's not a rectangle?
The formula works because any parallelogram can be transformed into a rectangle of equal area by moving a triangular section from one end to the other. This transformation keeps the base and height the same, resulting in the same area as a rectangle with those dimensions.
8. How is the area formula for a triangle related to that of a parallelogram?
The area formula for a triangle (A = ½bh) is half that of a parallelogram (A = bh) because a triangle is essentially half of a parallelogram. If you draw a diagonal in a parallelogram, it creates two congruent triangles, each with half the area of the original parallelogram.
9. What's the relationship between the areas of a triangle and the parallelogram that shares the same base and height?
The area of a triangle is always half the area of a parallelogram with the same base and height. This is because a diagonal line in a parallelogram creates two congruent triangles, each with half the area of the original parallelogram.
10. How can you find the area of an irregular shape?
To find the area of an irregular shape, you can:
11. How does the concept of area apply in real-world situations?
Area is used in many real-world applications, such as:
12. Can a shape have an area of zero? If so, what would it look like?
Yes, a shape can have an area of zero. This would be a one-dimensional object like a line or a point. While these have length or position, they have no width, and thus no area. In practical terms, very thin objects might be treated as having effectively zero area for certain calculations.
13. How does the area of a triangle change if you double its base but halve its height?
If you double the base and halve the height of a triangle, its area remains the same. This is because:
14. What's the difference between the area of a shape and its cross-sectional area?
The area of a shape refers to the two-dimensional space it occupies. Cross-sectional area is the area of a slice through a three-dimensional object. For example, the area of a circle is its total flat surface, while the cross-sectional area of a cylinder could be the circular area you see when you cut it perpendicular to its length.
15. How can you find the height of a parallelogram if you know its area and base?
To find the height of a parallelogram when you know its area (A) and base (b), use the formula:
16. Why do we use square units to measure area?
We use square units because area is a two-dimensional measurement. Square units represent a perfect square with equal sides, making it easy to calculate and compare areas of different shapes. For example, 1 m² is a square that is 1 meter on each side.
17. Can two shapes with different perimeters have the same area?
Yes, two shapes can have different perimeters but the same area. For example, a rectangle measuring 4x6 units and a square measuring 5x5 units both have an area of 24 square units, but their perimeters are different (20 units and 20 units, respectively).
18. Why is the height (altitude) of a triangle sometimes drawn outside the triangle?
The height of a triangle is always perpendicular to the base. In obtuse triangles, this perpendicular line may fall outside the triangle. Regardless of where it's drawn, the height is the shortest distance from the opposite vertex to the base (or its extension).
19. How can you prove that the area of a triangle is half the product of its base and height?
You can prove this by:
20. What's the difference between the area of a shape and its surface area?
Area refers to the two-dimensional space within a single flat shape. Surface area is the total area of all surfaces of a three-dimensional object. For example, a cube has six square faces, so its surface area is the sum of the areas of all six faces.
21. What is the definition of area in geometry?
Area is the amount of space inside the boundary of a two-dimensional shape. It is measured in square units, such as square meters (m²) or square feet (ft²). Area represents how much surface a shape covers.
22. How is the area of a shape different from its perimeter?
Area measures the space inside a shape, while perimeter measures the distance around the outside of a shape. Area is measured in square units (e.g., cm²), while perimeter is measured in linear units (e.g., cm).
23. Why is it important to use the same units when calculating area?
Using the same units is crucial because area is calculated by multiplying two lengths. If different units are used, the result will be meaningless. For example, multiplying meters by feet doesn't give a standard unit of area. Always convert to the same unit before calculating.
24. How does changing the dimensions of a shape affect its area?
Changing dimensions affects area as follows:
25. Why doesn't the slant height of a parallelogram affect its area?
The slant height doesn't affect the parallelogram's area because the area depends on the perpendicular height and base length. The slant side can change without altering the perpendicular height, thus not affecting the space enclosed by the shape.
26. What's the relationship between the areas of similar triangles?
The areas of similar triangles are proportional to the square of the ratio of their corresponding sides. If one triangle has sides twice as long as another similar triangle, its area will be four times larger. This is because area scales with two dimensions, not just one.
27. How does the area of a triangle change if you move one of its vertices?
Moving a vertex of a triangle can change its area in several ways:
28. Why is the formula for the area of a triangle (½bh) considered more useful than using Heron's formula?
The formula ½bh is generally more useful because:
29. How can you find the area of a triangle if you only know its three side lengths?
You can use Heron's formula:
30. How does the concept of area relate to integration in calculus?
In calculus, integration is used to find the area under a curve. The definite integral represents the accumulated area between the function and the x-axis over a specific interval. This concept extends the idea of area from simple geometric shapes to more complex curves and regions.
31. Can a shape have a negative area? Why or why not?
In standard geometry, area is always positive or zero. Negative areas don't have a physical meaning in real space. However, in some advanced mathematical contexts, like vector calculus or physics, negative areas might be used to represent direction or orientation, but this is a more abstract concept.
32. How does the area of a triangle change if you double all of its sides?
If you double all sides of a triangle, its area increases by a factor of four. This is because:
33. Why is it sometimes easier to find the area of an irregular shape by subtracting known areas?
Subtracting known areas can be easier for irregular shapes because:
34. How does the concept of area apply to curved shapes like circles?
For curved shapes like circles, the concept of area still applies, but the formulas are different:
35. What's the relationship between the area of a triangle and the radius of its circumscribed circle?
The relationship is given by the formula:
36. How can you find the area of a quadrilateral that's not a parallelogram?
To find the area of a general quadrilateral:
37. Why is the area of a shape always expressed in square units?
Area is expressed in square units because:
38. How does the area of a triangle relate to its angles?
The area of a triangle is related to its angles through the sine function:
39. What's the difference between using the formula A = ½bh and A = ½ab sin(C) for triangle area?
Both formulas calculate triangle area, but they're useful in different situations:
40. How can you find the area of a triangle if you only know its three vertices' coordinates?
You can use the formula:
41. Why doesn't changing the order of multiplication affect the area calculation?
Changing the order of multiplication doesn't affect area calculation because:
42. How does the concept of area extend to three-dimensional objects?
For 3D objects, we consider two types of area:
43. What's the relationship between the areas of the three triangles formed by an altitude of a larger triangle?
When an altitude is drawn in a triangle:
44. How does the area of a parallelogram change if you shear it (i.e., slide one side parallel to the opposite side)?
Shearing a parallelogram doesn't change its area because:
45. Why is the area of a triangle always less than or equal to half the product of any two of its sides?
This is true because:
46. How can you use area to prove the Pythagorean theorem?
One proof using area:
47. What's the relationship between the area of a triangle and its semiperimeter?
The relationship is given by Heron's formula:
48. How does the area of a regular polygon relate to the number of its sides?
For a regular polygon with n sides, radius r (distance from center to vertex), and side length s:
Also Read
Area - Definition, Area of Shapes Formula
02 Jul'25 05:32 PM
Area of Quadrilateral - Introduction, Formulae, Calculations
02 Jul'25 05:32 PM
Area of Isosceles Triangle - (Formulas, Derivation and Examples)
02 Jul'25 05:20 PM
Area of Parallelogram (Definition, Formulas & Examples)
02 Jul'25 05:20 PM
Area of Rectangle - Definition, Formula, Derivation and Examples
02 Jul'25 05:20 PM
Area Of Equilateral Triangle
02 Jul'25 05:19 PM
Area of Square Formula and Solved Examples
02 Jul'25 05:13 PM
Articles
Jul 03, 2025
Questions related to
Have a question related to ?
With a 25935 AP EAMCET bipc rank and 1620 in the local area (SC, women, non-farmer), your chances for an AgBSc seat in SVU Tirupati are low, as cutoff ranks for SC(non-farmer) in top colleges usually close much earlier. You may get in private or other government colleges.
Swastika Das 12 July,2025
With an AP EAMCET rank of 15,199 and a local area category female ranking of 305, it's unlikely you'll secure a free seat (government seat) in B.Sc. Agriculture at SVU Tirupati.
The cutoff ranks for free seats at SVU for Agriculture tend to be significantly lower.
However, you should still participate in the counselling process as there might be opportunities in private colleges or under management quota seats.
Thanks
Anushree Thakare 09 July,2025
Yes, you have a chance for a free seat in some government colleges under OBC and female quota, depending on cutoff and course availability.
Bipasha 05 July,2025
Hello,
Yes, BVRIT College at Narsapur has a prayer room on campus where Muslim students can offer their prayers. They do not have to leave the campus for it.
Hope it helps !
Prachi Kumari 26 June,2025
Hello,
Prachi Kumari 26 June,2025
News and Notifications
Back to top