Integration by Parts - Formula, Derivation, Applications, Examples

Integration by Parts is one of the important parts of Calculus, which applies to measuring the change in the function at a certain point. Mathematically, it forms a powerful tool by which slopes of functions are determined, the maximum and minimum of functions found, and problems on motion, growth, and decay, to name a few. These integration concepts have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

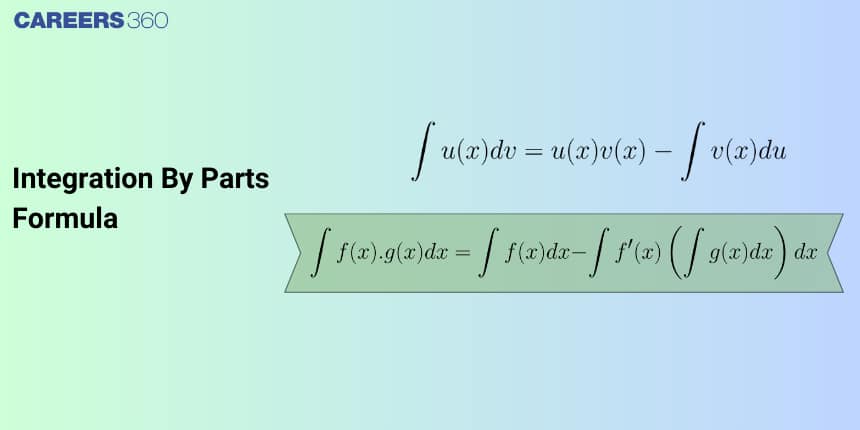
In this article, we will cover the concept of Integration by Part. This concept falls under the broader category of Calculus, a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), ten questions have been asked on this concept, including one in 2013, one in 2014, two in 2019, four in 2020, one in 2021, and one in 2022.

Integration By Parts:

Integration is the reverse process of differentiation. In integration, we find the function whose differential coefficient is given. The rate of change of a quantity y concerning another quantity x is called the derivative or differential coefficient of y concerning x. Geometrically, the Differentiation of a function at a point represents the slope of the tangent to the graph of the function at that point.

For example,

$\begin{aligned} & \frac{d}{d x}(\sin x)=\cos x \\ & \frac{d}{d x}\left(x^2\right)=2 x \\ & \frac{d}{d x}\left(e^x\right)=e^x\end{aligned}$

To evaluate the integration of a function which is a product of two functions, we use the method of integration by parts.

If two functions of x, u, and v are given,

where u is function of u(x),

v is function of v(x)

then

$\int u v d x=u \times \int v d x-\int\left\{\frac{d u}{d x} \int v d x\right\} d x$

i.e.

The integral of the product of two functions =

( first function) X ( integral of second function ) - integral of (differential of first function X integral of second function).

Proof:

Let, h(x) = f(x) . g(x), then by using the product rule, we obtain, h′(x) = f ′(x) g(x) + g′(x) f(x). Let’s now integrate both sides of this equation:

$\int h^{\prime}(x) d x=\int\left(g(x) f^{\prime}(x)+f(x) g^{\prime}(x)\right) d x$

this gives us,

$h(x)=f(x) g(x)=\int g(x) f^{\prime}(x) d x+\int f(x) g^{\prime}(x) d x$

Now we solve for $\int f(x) g^{\prime}(x) d x$

$\int f(x) g^{\prime}(x) d x=f(x) g(x)-\int g(x) f^{\prime}(x) d x$

By making the substitutions $u=f(x)$ and $v=g^{\prime}(x)$ which in turn make $g(x)=\int v d x$, we have the more compact form

$\int u v d x=u \int v d x-\int\left\{\frac{d u}{d x} \int v d x\right\} d x$

Important point for selecting first function (u) and second function (v)

Usually, we use the following preference order for selecting the first function. (Inverse, Logarithmic, Algebraic, Trigonometric, Exponential). In the above-stated order, the function on the left is always chosen as the first function. This rule is called ILATE.

For example, if an integral contains a logarithmic function and an algebraic function, we should choose the logarithmic function as the first function (u).

One of the interesting application of integration by part is:

$\int \mathrm{e}^{\mathbf{x}}\left\{\mathbf{f}(\mathbf{x})+\mathbf{f}^{\prime}(\mathbf{x})\right\} \mathrm{dx}=\mathrm{e}^{\mathbf{x}} \mathbf{f}(\mathbf{x})+\mathbf{C}$

Proof:
We have given $\int \mathrm{e}^x\left\{f(x)+f^{\prime}(x)\right\} d x$

$=\int \mathrm{e}^{\mathrm{x}} \cdot \mathrm{f}(\mathrm{x}) \mathrm{dx}+\int \mathrm{e}^{\mathrm{x}} \cdot \mathrm{f}^{\prime}(\mathrm{x}) \mathrm{dx}$

In first integral, take $f(x)$ as first function and $e^x$ as second function

$\begin{aligned}
& =f(x) \cdot e^x-\int f^{\prime}(x) \cdot e^x d x+\int e^x \cdot f^{\prime}(x) d x+C \\
& =f(x) \cdot e^x+C
\end{aligned}$

Thus, to evaluate the integrals of the type $\int e^x\left\{f(x)+f^{\prime}(x)\right\} d x$ we first express the integral as the sum of two integrals $\int e^x f(x) d x$ and $\int e^x f^{\prime}(x) d x$ and then integrate the integral involving $e^x f(x)$ as integral by parts taking $e^x$ as second function.

General Formula

$\int \mathrm{e}^{g(x)} \cdot\left\{f(x) g^{\prime}(x)+f^{\prime}(x)\right\} d x=f(x) \cdot e^{g(x)}+C$

Integration of $\int e^{a x} \cdot \sin (b x) d x$ and $\int e^{a x} \cdot \cos (b x) d x$
Let, $\quad \mathrm{I}=\int \mathrm{e}^{a x}(\sin b x) \mathrm{dx}$
take $\sin b x$ as first function and $\mathrm{e}^{a x}$ as second

$\begin{aligned}
& =\sin b x \cdot\left(\frac{e^{a x}}{a}\right)-\int b \cos b x \cdot \frac{e^{a x}}{a} d x \\
& =\frac{1}{a} \sin b x \cdot e^{a x}-\frac{b}{a}\left\{\cos b x \cdot \frac{e^{a x}}{a}-\int(-b \sin b x) \cdot \frac{e^{a x}}{a} d x\right\} \\
& =\frac{1}{a} \sin b x \cdot e^{a x}-\frac{b}{a^2} \cos b x \cdot e^{a x}-\frac{b^2}{a^2} \int \sin b x \cdot e^{a x} d x \\
I & =\frac{1}{a} \sin b x \cdot e^{a x}-\frac{b}{a^2} \cos b x \cdot e^{a x}-\frac{b^2}{a^2} I \\
\therefore \quad I+\frac{b^2}{a^2} I & =\frac{1 \cdot e^{a x}}{a^2} \cdot(a \sin b x-b \cos b x) \\
\Rightarrow \quad I & =\frac{e^{a x}}{a^2+b^2}(a \sin b x-b \cos b x)+C
\end{aligned}$

In the same way,

$\int e^{a x} \cos b x d x=\frac{e^{a x}}{a^2+b^2}(a \cos b x+b \sin b x)+C$
Result for integration by parts or ex :

$\begin{aligned}
& \int e^{\tan ^{-1} x}\left[\frac{x^n+1}{x^2+1}+n x^{n-1}\right] d x=e^{\tan ^{-1} x}\left(x^n+1\right)+c \\
& \int e^{g(x)}\left\{f(x) g^{\prime}(x)+f^{\prime}(x)\right\} d x=f(x) \cdot e^{g(x)}+C
\end{aligned}$
developments in many scientific and engineering disciplines.

Recommended Video Based on Integration by Parts

Solved Examples Based On Integration by Parts:

Example 1: The integral $\int x \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right) d x(x>0)$ is equal to:
${ }_1-x+\left(1+x^2\right) \tan ^{-1} x+c$
2) $x-\left(1+x^2\right) \cot ^{-1} x+c$
3) $-x+\left(1+x^2\right) \cot ^{-1} x+c$
4) $x-\left(1+x^2\right) \tan ^{-1} x+c$

Solution

As learned in the concept

Integration By PARTS -

Let $u$ and $v$ are two functions then

$
\int u \cdot v d x=u \int v d x-\int\left(\frac{d u}{d x} \int v d x\right) d x
$

- wherein

Where $u$ is the lst function $v$ is the Ind function

$
\begin{aligned}
& \text { Put } x=\tan \theta ; d x=\sec ^2 \theta d \theta \\
& \int x \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right) d x(x>0) \\
& \int \tan \theta\left[\cos ^{-1}\left(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right)\right]\left(\sec ^2 \theta d \theta\right) \\
& \int \tan \theta\left[\cos ^{-1}(\cos 2 \theta)\right]\left(\sec ^2 \theta d \theta\right) \\
& \int \tan \theta \cdot 2 \theta \sec ^2 \theta d \theta=2 \int \theta\left(\tan \theta \sec ^2 \theta\right) d \Theta
\end{aligned}
$

Put $\tan \theta=t$ we get $\sec ^2 \theta d \theta=d t$

$
\begin{aligned}
& 2 \int \tan ^{-1} t(t) d t \\
& 2 \int t \cdot \tan ^{-1} t \cdot d t
\end{aligned}
$

Using by parts

$\begin{aligned}
& 2\left[\frac{t^2}{2} \cdot \tan ^{-1} t-\int \frac{1}{1+t^2} \cdot \frac{t^2}{2} \cdot d t\right] \\
& t^2 \cdot \tan ^{-1} t-\int \frac{1}{1+t^2} \cdot t^2 \cdot d t \\
& t^2 \cdot \tan ^{-1} t-\int \frac{t^2+1-1}{1+t^2} \cdot d t \\
& t^2 \cdot \tan ^{-1} t-\int\left[1-\frac{1}{1+t^2}\right] \cdot d t \\
& t^2 \cdot \tan ^{-1} t-\left[t-\tan ^{-1} t\right] \\
& \Rightarrow x=t \\
& x=\tan \theta \quad \& \quad \tan \theta=t \\
& \int x \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right) d x=x^2 \tan ^{-1} x-x+\tan ^{-1} x+C
\end{aligned}$
Hence, the answer is the option 1.

Example 2: If $\int f(x) d x=\Psi(x)$, then $\int x^5 f\left(x^3\right) d x$ is equal to:
1) $\frac{1}{3}\left[x^3 \Psi\left(x^3\right)-\int x^3 \Psi\left(x^3\right) d x\right]+C$
2) $\frac{1}{3}\left[x^3 \Psi\left(x^3\right)-\int x^2 \Psi\left(x^3\right) d x\right]+C$
3) $\frac{1}{3} x^3 \Psi\left(x^3\right)-3 \int x^3 \Psi\left(x^3\right) d x+C$
4) $\frac{1}{3} x^3 \Psi\left(x^3\right)-\int x^2 \Psi\left(x^3\right) d x+C$

Solution
Using Integration By Parts,

$\begin{aligned}
& \int f(x) d x=\Psi(x) \int x^5 f\left(x^3\right) d x=\frac{1}{3} \int\left(3 x^2\right) \cdot x^3 f\left(x^3\right) d x P u t x^3=t ; 3 x^2 d x=d t \\
& \frac{1}{3} \int t f(t) d t=\frac{1}{3}\left[t \int f(t) d t-\int 1 \int f(t) d t\right]
\end{aligned}$

Replace $t$ by $x^3$

$I=\frac{1}{3} x^3 \Psi\left(x^3\right)-\frac{1}{3} \int \Psi\left(x^3\right) d t=\frac{1}{3} x^3 \Psi\left(x^3\right)-\frac{1}{3} \int 3 x^2 d x . \Psi\left(x^3\right)=\left[\frac{1}{3} x^3 \Psi\left(x^3\right)-\int x^2 \Psi\left(x^3\right) d x\right]+c$
Hence, the answer is the option (4).

Example 3: Let $f(x)=\int \frac{\sqrt{x}}{(1+x)^2} d x(x \geqslant 0)$.Then $f(3)-f(1)$ is equal to:
1) $-\frac{\pi}{12}+\frac{1}{2}+\frac{\sqrt{3}}{4}$
2) $\frac{\pi}{6}+\frac{1}{2}+\frac{\sqrt{3}}{4}$
3) $-\frac{\pi}{6}+\frac{1}{2}+\frac{\sqrt{3}}{4}$
4) $\frac{\pi}{12}+\frac{1}{2}-\frac{\sqrt{3}}{4}$

Solution
$f(x)=\int_1^3 \frac{\sqrt{x} d x}{(1+x)^2}=\int_1^{\sqrt{3}} \frac{t \cdot 2 t d t}{\left(1+t^2\right)^2}($ put $\sqrt{x}=t)$
$=\left(-\frac{t}{1+t^2}\right)_t^{\sqrt{3}}+\left(\tan ^{-1} t\right)_1^{\sqrt{3}}$ [Applying by parts ]
$=-\left(\frac{\sqrt{3}}{4}-\frac{1}{2}\right)+\frac{\pi}{3}-\frac{\pi}{4}$
$=\frac{1}{2}-\frac{\sqrt{3}}{4}+\frac{\pi}{12}$

Hence, the answer is the option 4.

Example 4: The integral $\int\left(\frac{x}{x \sin +\cos x}\right)^2 d x$ is equal to (where C is constant of integration).
1) $\tan x-\frac{x \sec x}{x \sin x+\cos x}+C$
2) $\sec x \frac{x \tan x}{x \sin x+\cos x}+C$
3) $\sec x-\frac{x \tan x}{x \sin x+\cos x}+C$
4) $\tan x+\frac{x \sec x}{x \sin x+\cos x}+C$

Solution

$\begin{aligned}
& \int\left(\frac{x}{x \sin x+\cos x}\right)^2 d x=\int\left(\frac{x}{\cos x}\right) \cdot \frac{x \cos x d x}{(x \sin x+\cos x)^2} \\
& =\frac{x}{\cos x}\left(-\frac{1}{x \sin x+\cos x}\right)+\int\left(\frac{\cos x+x \sin x}{\cos ^2 x}\right)\left(\frac{1}{x \sin x+\cos x}\right) d x \\
& =-\frac{x \sec x}{x \sin x+\cos x}+\int \sec ^2 x d x \\
& =-\frac{x \sec x}{x \sin x+\cos x}+\tan x+C
\end{aligned}$
Hence, the answer is option (1).

Example 5 :

$\int_{\mathrm{If}}^1\left(e^{2 x}+2 e^x-e^{-x}-1\right) e^{\left(e^x+e^{-x}\right)} d x=g(x) e^{\left(e^x+e^{-x}\right)}+c$

1) e
2) $e^2$
3) 1
4) 2

Solution:

$\begin{aligned}
& e^{2 x}+2 e^x-e^{-x}-1 \\
& =e^x\left(e^x+1\right)-e^{-x}\left(e^x+1\right)+e^x \\
& \left.=\left[\left(e^x+1\right)\right]\left(e^x-e^{-x}\right)+e^x\right] \\
& \text { so } I=\int\left(e^x+1\right)\left(e^x-e^{-x}\right) e^{e^x+e^{-x}}+\int e^x \cdot e^{e^x+e^{-x}} d x \\
& =\left(e^x+1\right) e^{e^x+e^{-x}}-\int e^x \cdot e^{e^x+e^{-x}} d x+\int e^x \cdot e^{e^x+e^{-x}} d x \\
& =\left(e^x+1\right) e^{e^x+e^{-x}}+C \\
& \therefore g(x)=e^x+1 \Rightarrow g(0)=2
\end{aligned}$

Hence, the answer is option (4).