Law of Cosines: Proof and Examples

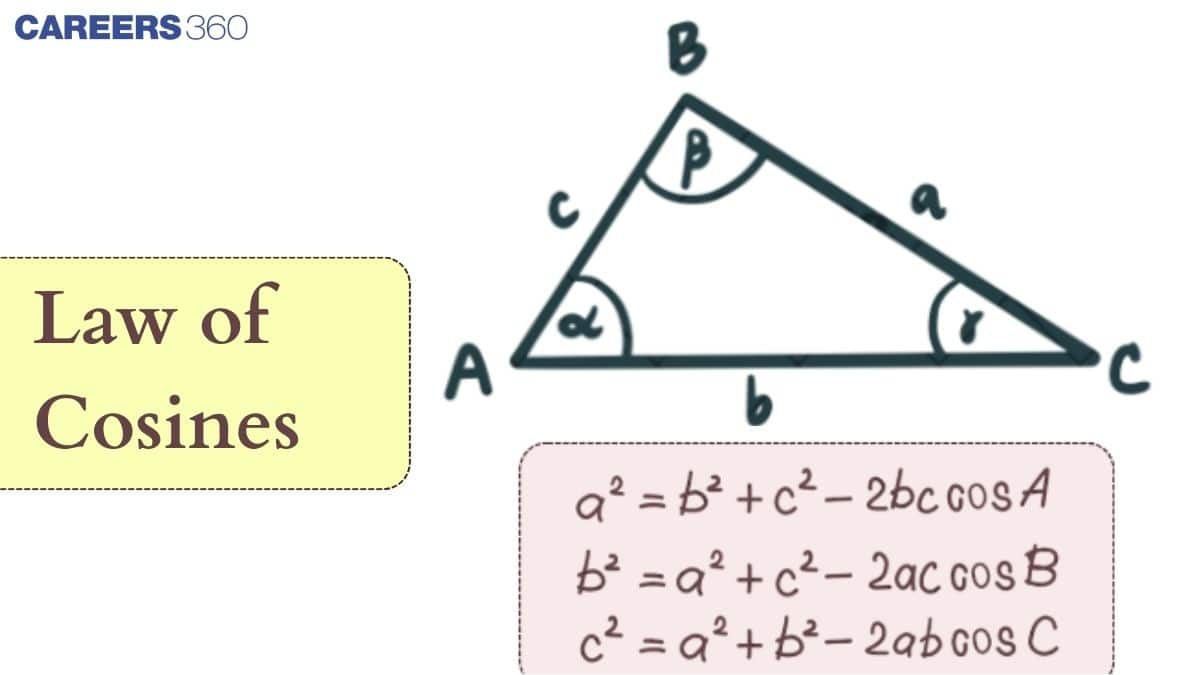
Overview of a Triangle

A triangle is a polygon with three sides. It is considered more special than other polygons because it has the fewest number of sides among all polygons. A triangle consists of six main elements: three sides and three angles. Several important rules and theorems connect the sides and angles of a triangle.

Some standard symbols used to represent the elements of a triangle are as follows:

In △ABC, the angles are denoted by capital letters A,B, and C, while the sides opposite to these angles are represented by the small letters a,b, and c respectively.

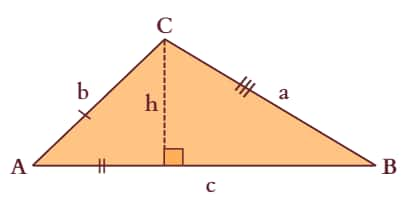
The following standard notations are universally used in relation to △ABC:

Angles: $∠BAC = ∠A$, $∠ABC = ∠B$, $∠BCA = ∠C$

Sides: $AB = c$, $AC = b$, $BC = a$

The semi-perimeter of △ABC is given by:

$s = \dfrac{a + b + c}{2}$

The perimeter of △ABC is:

$2s = a + b + c$

The area of a triangle is usually denoted by $S$ or $Δ$.

For any △ABC, the following properties hold:

$∠A + ∠B + ∠C = 180^\circ$

$a + b > c$, $b + c > a$, $c + a > b$ (Triangle inequalities)

$a > 0$, $b > 0$, $c > 0$

Introduction to Law of Cosines

The Law of Cosines is one of the most important results in trigonometry, often used when the Law of Sines cannot directly solve a triangle. It gives a direct relation between the sides and angles of any triangle, which makes it highly useful in Class 11 and Class 12 mathematics, as well as in competitive exams like JEE Main and CUET. Below, we explore the basics and how it connects with the Law of Sines.

What is the Law of Cosines?

The Law of Cosines states that in any triangle, the square of one side is equal to the sum of the squares of the other two sides, minus twice the product of those two sides and the cosine of the included angle.

The Law of Cosines formula connects the three sides of a triangle with the cosine of one of its angles. For a triangle $ABC$ with sides $a, b, c$ opposite to angles $\angle A, \angle B, \angle C$ respectively, the formula is:

$c^2 = a^2 + b^2 - 2ab \cos \angle C$

Similarly, we can write:

$a^2 = b^2 + c^2 - 2bc \cos \angle A$

$b^2 = a^2 + c^2 - 2ac \cos \angle B$

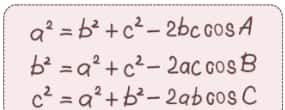
This formula generalises the Pythagoras Theorem, because when $C=90^\circ, \cos⁡ C=0$, giving $c^2=a^2+b^2$.

Proof of Law of Cosines

Drop a perpendicular from point C to the x-axis. Let this perpendicular be the altitude (height).

From basic trigonometric identities, we know:

$\cos \theta = \dfrac{x \, (\text{adjacent})}{b \, (\text{hypotenuse})}, \quad

\sin \theta = \dfrac{y \, (\text{opposite})}{b \, (\text{hypotenuse})}$

Thus, $x = b \cos \theta$ and $y = b \sin \theta$.

So, the coordinates of point $C$ are $(b \cos \theta, \, b \sin \theta)$.

Now, using side $(x - c)$ as one leg of a right triangle and $y$ as the other leg, we apply the Pythagoras theorem to find side $a$:

$a^2 = (x - c)^2 + y^2$

Substitute $x = b \cos \theta$ and $y = b \sin \theta$:

$a^2 = (b \cos \theta - c)^2 + (b \sin \theta)^2$

Expand: $a^2 = (b^2 \cos^2 \theta - 2bc \cos \theta + c^2) + b^2 \sin^2 \theta$

Group terms:

$a^2 = b^2 \cos^2 \theta + b^2 \sin^2 \theta + c^2 - 2bc \cos \theta$

Since $\cos^2 \theta + \sin^2 \theta = 1$:

$a^2 = b^2 (1) + c^2 - 2bc \cos \theta$

Therefore, $a^2 = b^2 + c^2 - 2bc \cos \theta$

Now, since $\theta$ is the measure of $\angle A$ in $\triangle ABC$:

$a^2 = b^2 + c^2 - 2bc \cos \angle A$

Rearranging gives another form:

$\cos \angle A = \dfrac{b^2 + c^2 - a^2}{2bc}$

The same derivation holds whether $\angle A$ is acute, right, or obtuse.

Similarly, we can write:

$b^2 = a^2 + c^2 - 2ac \cos \angle B$,

$c^2 = a^2 + b^2 - 2ab \cos \angle C$

Note:

If the lengths of all three sides of a triangle are known, we can calculate each angle using the Law of Cosines.

If two sides (say $b$ and $c$) and the included angle $\angle A$ are given, we can first find the third side $a$ using the cosine rule:

$a^2 = b^2 + c^2 - 2bc \cos \angle A$

or equivalently,

$\cos \angle A = \dfrac{b^2 + c^2 - a^2}{2bc}$

Once $a$ is determined, and since $a, b, c$ are known, we can then use the Law of Cosines again to find the other angles $\angle B$ and $\angle C$.

Applications of the Law of Cosines

The Law of Cosines is not limited to solving textbook problems; it has wide applications in geometry, trigonometry, and even real-world scenarios like physics and engineering. It helps in determining unknown sides, angles, and solving oblique triangles. Below are some key applications you should know.

Solving Oblique Triangles

Like Law of Sines, the Law of Cosines is especially useful for solving oblique triangles (triangles that are not right-angled). Unlike the Pythagoras Theorem, which applies only to right triangles, the cosine rule works for acute and obtuse triangles as well.

• If the three sides of a triangle $(a, b, c)$ are given, we can calculate any angle using: $\cos \angle A = \dfrac{b^2 + c^2 - a^2}{2bc}$

• This makes the Law of Cosines an important part in trigonometry because it allows us to determine angles without requiring right angles.

Finding Unknown Sides and Angles

The Law of Cosines also helps when we need to calculate missing sides:

• If two sides and the included angle are known (SAS case), the third side can be calculated using: $a^2=b^2+c^2−2bc \cos⁡ A$

• Once one side is found, we can apply the same law to determine the remaining angles.

• This makes it highly efficient for triangle-solving problems where the Law of Sines alone might not be sufficient (for example, in the ambiguous case of SSA).

Solved Examples Based on Cosine Rule

Example 1: In a triangle ABC, if cos A + 2 cos B + cos C = 2 and the lengths of the sides are opposite to the angles A and C are 3 and 7 respectively, then cos A – cos C is equal to: [JEE MAINS 2023]

Solution:

$\cos A + \cos C = 2(1 - \cos B)$

$2 \cos \dfrac{A + C}{2} \cos \dfrac{A - C}{2} = 4 \sin^2 \dfrac{B}{2}$

As $\cos \dfrac{A + C}{2} = \sin \dfrac{B}{2}$

So, $\cos \dfrac{A - C}{2} = 2 \sin \dfrac{B}{2}$

$2 \cos \dfrac{B}{2} \cos \dfrac{A - C}{2} = 4 \sin \dfrac{B}{2} \cos \dfrac{B}{2}$

$2 \sin \dfrac{A + C}{2} \cos \dfrac{A - C}{2} = 4 \sin \dfrac{B}{2} \cos \dfrac{B}{2}$

$\sin A + \sin C = 2 \sin B$

$a + c = 2b \Rightarrow a = 3, c = 7, b = 5$

$\cos A - \cos C = \dfrac{b^2 + c^2 - a^2}{2bc} - \dfrac{a^2 + b^2 - c^2}{2ab}$

$= \dfrac{25 + 49 - 9}{70} - \dfrac{9 + 25 - 49}{30}$

$= \dfrac{65}{70} + \dfrac{15}{30}$

$= \dfrac{65}{70} + \dfrac{1}{2}$

$= \dfrac{65}{70} + \dfrac{35}{70}$

$= \dfrac{100}{70} = \dfrac{10}{7}$

Hence, the answer is $\dfrac{10}{7}$.

Example 2: Given b+c11=c+a12=a+b13 for a △ABC with usual notation.If cos⁡Aα=cos⁡Bβ=cos⁡Cγ, then the ordered triad (α,β,γ) has a value: [JEE MAINS 2019]
Solution:

Given: $b + c = 11\lambda$, $a + c = 12\lambda$, $a + b = 13\lambda$

From these, solving for sides:

$a = 7\lambda$, $b = 6\lambda$, $c = 5\lambda$

Using the Cosine Rule:

$\cos A = \dfrac{b^2 + c^2 - a^2}{2bc} = \dfrac{15}{?}$

$\cos B = \dfrac{a^2 + c^2 - b^2}{2ac} = \dfrac{19}{35}$

$\cos C = \dfrac{a^2 + b^2 - c^2}{2ab} = \dfrac{5}{7}$

Thus, $\alpha : \beta : \gamma = 7 : 19 : 25$

Example 3: The angle of elevation of the top of a vertical tower from a point P on the horizontal ground was observed to be α After moving a distance 2 meters from P towards the foot of the tower, the angle of elevation changes to β Then the height of the tower (in meters) is [JEE MAINS 2014]

Solution:

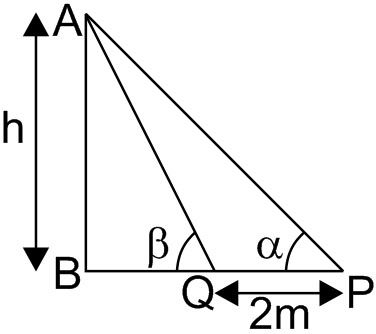
In $\triangle APB$, $\tan \alpha = \dfrac{AB}{BP}$

$\Rightarrow BP = \dfrac{h}{\tan \alpha} = h \dfrac{\cos \alpha}{\sin \alpha}$

In $\triangle AQB$, $\tan \beta = \dfrac{AB}{BQ}$

$\Rightarrow BQ = \dfrac{h}{\tan \beta} = h \dfrac{\cos \beta}{\sin \beta}$

Now, $PQ = 2$

$\Rightarrow PB - QB = 2$

$\Rightarrow h \left( \dfrac{\cos \alpha}{\sin \alpha} - \dfrac{\cos \beta}{\sin \beta} \right) = 2$

$\Rightarrow h \dfrac{\sin(\beta - \alpha)}{\sin \alpha \sin \beta} = 2$

$\Rightarrow h = \dfrac{2 \sin \alpha \sin \beta}{\sin(\beta - \alpha)}$

Hence, the answer is $\dfrac{2 \sin \alpha \sin \beta}{\sin(\beta - \alpha)}$.

Example 4: Let 10 vertical poles standing at equal distances on a straight line, subtend the same angle of elevation α at a point O on this line and all the poles are on the same side of O. If the height of the longest pole is ‘h’ and the distance of the foot of the smallest pole from O is ‘a’, then the distance between two consecutive poles is [JEE MAINS 2015]

Solution:

For all poles to subtend the same angle, the longest pole must be farthest, the smallest pole must be nearest, while all other poles are arranged in ascending order of height. Let the distance between 2 consecutive poles be x. Then,

$B_1B_{10} = 9x$

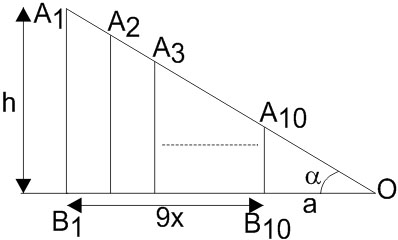
In $\triangle A_1B_1O$, $\tan \alpha = \dfrac{A_1B_1}{B_1O} = \dfrac{h}{B_1O}$

$B_1O = 9x + a$

$\tan \alpha = \dfrac{h}{9x + a}$

$\sin \alpha \cos \alpha = \dfrac{h}{9x + a}$

$\Rightarrow 9x \sin \alpha + a \sin \alpha = h \cos \alpha$

$\Rightarrow x = \dfrac{h \cos \alpha - a \sin \alpha}{9 \sin \alpha}$

Hence, the answer is $\dfrac{h \cos \alpha - a \sin \alpha}{9 \sin \alpha}$.

Example 5: Let a vertical tower AB have its end A on the level ground. Let C be the mid-point of AB and P be a point on the ground such that AP=2AB. If ∠BPC=β, then tan β is equal to : [JEE MAINS 2017]
Solution:

Height and Distances -The height or length of an object or the distance between two distant objects can be determined with the help of trigonometric ratios.

Let, $AC=CB=h, AB=2h$ and $AP=4h$

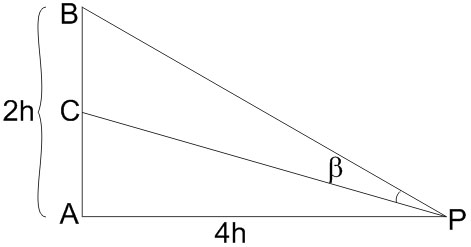
Now, $\tan \angle BPA = \dfrac{2h}{4h} = \dfrac{1}{2}$

$\tan \angle CPA = \dfrac{h}{4h} = \dfrac{1}{4}$

$\tan \beta = \tan(\angle BPA - \angle CPA)$

$= \dfrac{\tan(\angle BPA) - \tan(\angle CPA)}{1 + \tan(\angle BPA)\tan(\angle CPA)}$

$= \dfrac{\tfrac{1}{2} - \tfrac{1}{4}}{1 + \tfrac{1}{2}\cdot\tfrac{1}{4}}$

$= \dfrac{\tfrac{1}{4}}{1 + \tfrac{1}{8}}$

$= \dfrac{\tfrac{1}{4}}{\tfrac{9}{8}}$

$= \dfrac{1}{4} \cdot \dfrac{8}{9} = \dfrac{2}{9}$

Thus, $\tan \beta = \dfrac{2}{9}$

Hence, the answer is $\dfrac{2}{9}$.

List of Topics related to Law of Cosines

The Law of Cosines is closely linked with several other trigonometric concepts that strengthen problem-solving and extend its applications. Exploring these areas gives a more complete understanding of trigonometry. Below are the related topics you can study.

NCERT Resources

For a solid grasp of trigonometric functions, NCERT study materials are among the most dependable references. They simplify concepts, provide structured practice, and help in systematic exam preparation. Below are the NCERT resources for Chapter 3: Trigonometric Functions.

NCERT Class 11 Maths Notes for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Solutions for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Exemplar Solutions for Chapter 3 - Trigonometric Functions

Practice Questions based on Law of Cosines

Practising different types of trigonometric questions is the best way to strengthen concepts and improve accuracy. Practising MCQs not only builds confidence but also prepares you for exam based problems. Below are the practice topics you can try.

Law of Cosines - Practice Question MCQ

You can practice the related questions from the links shared below: