Important Solutions of Triangle Formulas

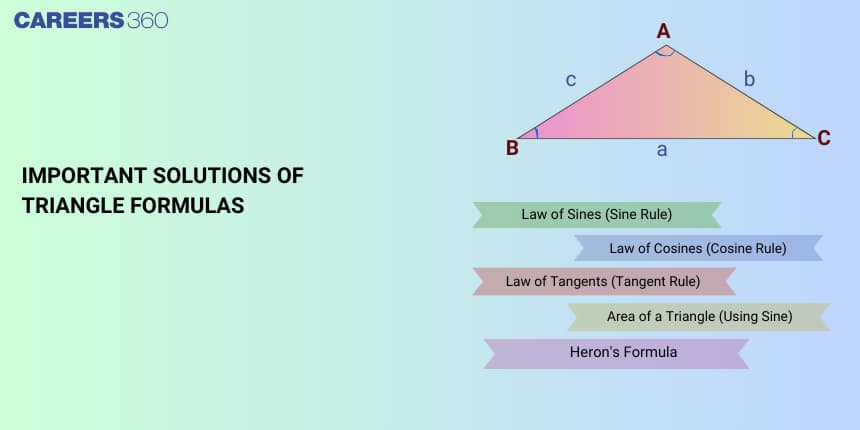
Elements of a Triangle (Sides, Angles, Vertices)

A triangle is defined by three sides, three angles, and three vertices. If the vertices are denoted as $A$, $B$, and $C$, then the sides opposite to them are represented as $a$, $b$, and $c$ respectively. Thus, side $a = BC$, side $b = AC$, and side $c = AB$. These notations are widely used in triangle formulas for solving problems in geometry and trigonometry.

The sum of all interior angles of a triangle is always $180^\circ$, which can be written as:

$ \angle A + \angle B + \angle C = 180^\circ $

The perimeter of the triangle is the sum of its sides:

$ P = a + b + c $

The semi-perimeter is:

$ s = \dfrac{a+b+c}{2} $

These notations and formulas are the foundation for advanced results such as Heron’s Formula, sine rule, and cosine rule. For example, when solving for the area or radius of incircle/excircle, knowing the sides $a, b, c$ and the semi-perimeter $s$ is essential.

There are different cases that arise when a few components of the triangle are given.

Different Cases in Solving a Triangle

When certain components (sides or angles) of a triangle are given, the remaining unknowns can be determined using standard trigonometric formulas. Below are the main cases:

Case 1: When three sides $(a, b, c)$ are given

The remaining quantities can be found as follows:

$\begin{array}{|c|c|} \hline \text{Given} & \text{To Determine} \\ \hline a, b, c & (i) \text{Area: } \Delta = \sqrt{s(s-a)(s-b)(s-c)}, \quad \text{where } s = \frac{a+b+c}{2} \\ \hline & (ii) \text{Angles using cosine rule: } \cos A = \frac{b^2 + c^2 - a^2}{2bc}, \quad \cos B = \frac{a^2 + c^2 - b^2}{2ac} \\ & \quad \text{and } C = 180^\circ - A - B \\ \hline & (iii) \text{Angles using half–angle formula: } \tan \frac{A}{2} = \sqrt{\frac{(s-b)(s-c)}{s(s-a)}} \\ \hline \end{array}$

Case 2: When two sides and the included angle are given

Suppose $a, b$ and $\angle C$ are given.

$\begin{array}{|c|c|} \hline \text{Given} & \text{To Determine} \\ \hline a, b, \angle C & (i) \text{Third side using cosine rule: } c^2 = a^2 + b^2 - 2ab \cos C \\ \hline & (ii) \text{Second angle: } \cos A = \frac{b^2 + c^2 - a^2}{2bc} \\ \hline & (iii) \text{Area: } \Delta = \tfrac{1}{2} ab \sin C \\ \hline \end{array}$

Case 3: When one side and two angles are given

Suppose $a$, $\angle A$, and $\angle B$ are given.

$\begin{array}{|c|c|} \hline \text{Given} & \text{To Determine} \\ \hline a, \angle A, \angle B & (i) \text{Third angle: } \angle C = 180^\circ - (A + B) \\ \hline & (ii) \text{Other sides using sine rule: } b = a \cdot \frac{\sin B}{\sin A}, \quad c = a \cdot \frac{\sin C}{\sin A} \\ \hline & (iii) \text{Area: } \Delta = \tfrac{1}{2} ab \sin C \\ \hline \end{array}$

Case 4: When two sides and an angle opposite to one of them are given

Suppose $a, b$, and $\angle A$ are given.

Using the sine rule:

$\sin B = \frac{b}{a} \sin A$

Now, three possibilities occur:

1. If $\dfrac{b}{a}\sin A > 1$ (or $a < b \sin A$)
   $\quad \Rightarrow \sin B > 1$, which is impossible.
   Hence, no triangle exists.

2. If $\dfrac{b}{a}\sin A = 1$
   $\quad \Rightarrow \sin B = 1 \Rightarrow B = 90^\circ$
   Hence, a unique right-angled triangle is possible.

3. If $\dfrac{b}{a}\sin A < 1$ (or $a > b \sin A$)
   $\quad \Rightarrow B$ is valid and two triangles may exist (Ambiguous Case).
   The third angle can then be found as:

   $C = 180^\circ - (A + B)$

Area and Perimeter Formulas of a Triangle

The formulas for area and perimeter of a triangle are the foundation of triangle geometry. From the basic perimeter formula $P = a + b + c$ to advanced expressions like Heron’s formula, these relations help in solving geometry and trigonometry problems efficiently. These triangle area formulas are also widely used in competitive exams and applied mathematics.

Formula for Perimeter and Semi-Perimeter

The perimeter of a triangle is the sum of all its sides, while the semi-perimeter is half of it. These are often used in advanced formulas like Heron’s formula for area.

• Perimeter: $P = a + b + c$

• Semi-perimeter: $s = \dfrac{a + b + c}{2}$

Heron’s Formula for Area of a Triangle

When all three sides of a triangle are known, Heron’s formula is the most direct way to find its area.

• Formula: $A = \sqrt{s(s-a)(s-b)(s-c)}$

• Here $s$ is the semi-perimeter and $a, b, c$ are side lengths.

Area Formulas Using Trigonometry

Trigonometric identities help in finding the area of a triangle when sides and angles are known.

• Using sine: $A = \dfrac{1}{2} ab \sin C$

• Using circumradius: $A = \dfrac{abc}{4R}$

• Using inradius: $A = sr$

Pythagoras Theorem in Right Triangles

For a right triangle: $c^2 = a^2 + b^2$

It is one of the most widely used theorems in mathematics, engineering, and physics applications.

Area of $\triangle ABC$ using trigonometry

$\Delta = \frac{1}{2} \, b \cdot c \cdot \sin A$

Similarly,

$\Delta = \frac{1}{2} \, a \cdot b \cdot \sin C = \frac{1}{2} \, c \cdot a \cdot \sin B$

Laws and Rules in Triangle Geometry

Triangle geometry relies heavily on trigonometric laws such as the Law of Sines, Law of Cosines, and Law of Tangents. These rules are essential for solving problems where sides and angles are interdependent. They provide direct relations between sides and angles, making them highly useful in both theoretical and applied mathematics.

Law of Sines

The Law of Sines establishes a direct ratio between the sides of a triangle and the sines of their opposite angles. It is particularly useful when two angles and one side, or two sides and a non-included angle, are known.

• Formula: $\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R$

Law of Cosines

The Law of Cosines is an extension of the Pythagoras theorem, applicable to any triangle. It helps in finding an unknown side or angle when other elements are known.

• Formula: $a^2 = b^2 + c^2 - 2bc \cos A$

• Similarly: $b^2 = a^2 + c^2 - 2ac \cos B$ and $c^2 = a^2 + b^2 - 2ab \cos C$

Law of Tangents

The Law of Tangents links the difference and sum of sides of a triangle with the tangent of half the sum and half the difference of angles.

• Formula: $\dfrac{a-b}{a+b} = \dfrac{\tan \dfrac{1}{2}(A-B)}{\tan \dfrac{1}{2}(A+B)}$

Inradius, Exradius, and Circumradius Formulas

The three special radii of a triangle—inradius (r), exradius (rₐ, r_b, r_c), and circumradius (R)—play a central role in advanced triangle geometry. These quantities connect triangle area, side lengths, and angles, and are widely used in coordinate geometry and trigonometric derivations.

Inradius Formula and Relation with Area

The inradius is the radius of the incircle that touches all three sides of a triangle. It relates the area of a triangle to its semi-perimeter.

• Formula: $r = \dfrac{\Delta}{s}$
  where $\Delta$ = area of the triangle, $s = \dfrac{a+b+c}{2}$

Another relation using angles:

• $r = \dfrac{a \tan \dfrac{B}{2} \tan \dfrac{C}{2}}{\tan \dfrac{B}{2} + \tan \dfrac{C}{2}}$

Exradius of a Triangle and Its Formulas

The exradius corresponds to the radius of an excircle that touches one side externally and the extensions of the other two sides. Each triangle has three exradii.

• Formula: $r_a = \dfrac{\Delta}{s-a}$, $r_b = \dfrac{\Delta}{s-b}$, $r_c = \dfrac{\Delta}{s-c}$

Circumradius Formula

The circumradius is the radius of the circumcircle that passes through all three vertices of the triangle. It connects side lengths with the opposite angles.

• Formula using sine rule: $R = \dfrac{a}{2\sin A} = \dfrac{b}{2\sin B} = \dfrac{c}{2\sin C}$

• Relation with sides: $R = \dfrac{abc}{4\Delta}$

Special Properties of Triangles

Every triangle has significant centers such as the centroid, orthocentre, incentre, and circumcentre. These points are defined using medians, altitudes, and angle bisectors, and they have specific coordinate formulas and geometric properties.

Medians and Centroid Formulas

A median is a line segment from a vertex to the midpoint of the opposite side. All three medians intersect at the centroid (G), which divides each median in a $2:1$ ratio.

• Median length from vertex $A$: $m_a = \dfrac{1}{2}\sqrt{2b^2 + 2c^2 - a^2}$

• Centroid coordinates: $G \left(\dfrac{x_1+x_2+x_3}{3}, \dfrac{y_1+y_2+y_3}{3}\right)$

Altitudes and Orthocentre Properties

An altitude is a perpendicular drawn from a vertex to the opposite side (or its extension). The three altitudes intersect at the orthocentre (H).

• Equation of altitude from $A(x_1,y_1)$ to $BC$: slope of $BC = m$, slope of altitude $= -\dfrac{1}{m}$

Angle Bisectors and Incentre Relations

An angle bisector divides the angle into two equal parts. The angle bisectors intersect at the incentre (I), which is also the center of the incircle.

• Internal angle bisector theorem: $\dfrac{AB}{AC} = \dfrac{BD}{DC}$

• Incentre coordinates: $I \left(\dfrac{ax_1+bx_2+cx_3}{a+b+c}, \dfrac{ay_1+by_2+cy_3}{a+b+c}\right)$

Advanced Triangle Formulas

Advanced triangle formulas extend beyond basic area and angle relations. These formulas bridge classical geometry with trigonometry and coordinate geometry for precise problem-solving.

Sine Rule for Heights and Area

$h_a = b \sin C = c \sin B$

Law of sines connects a triangle’s altitudes with its sides and angles, making it useful for finding area and perpendicular distances.

Cosine Rule for Angle Calculation

$\cos A = \dfrac{b^2 + c^2 - a^2}{2bc}$

The cosine rule allows direct calculation of an angle when the side lengths are known, a fundamental tool in trigonometry.

Half-Angle Formulas

• $\sin \dfrac{A}{2} = \sqrt{\dfrac{(s-b)(s-c)}{bc}}$

• $\cos \dfrac{A}{2} = \sqrt{\dfrac{s(s-a)}{bc}}$

• $\tan \dfrac{A}{2} = \sqrt{\dfrac{(s-b)(s-c)}{s(s-a)}}$

These relations simplify problems involving angle bisectors, incircles, and advanced area calculations.

Tangent Rule or Napier’s Analogy

$\dfrac{a+b}{c} = \dfrac{\cos \dfrac{1}{2}(A-B)}{\cos \dfrac{1}{2}(A+B)}$

Napier’s and Mollweide’s equations are advanced trigonometric identities that make solving oblique triangles faster and more elegant.

Coordinate Geometry Formulas for Triangle

Coordinate geometry offers a structured method to analyze triangles using Cartesian coordinates. It enables calculation of area, centroid, incentre, and other centers directly from vertex coordinates.

• Area of a Triangle Using Coordinates
  $A = \dfrac{1}{2}\left| x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2) \right|$

• Projection Formula
  $AB \cdot AC = |AB||AC|\cos \angle A$
  This connects vectors and triangle geometry, particularly in analytic geometry.

• In a triangle $ABC$, the projection of a side on another side is given by:

  $c = a \cos B + b \cos A$

  Similarly,

  $a = b \cos C + c \cos B$

  $b = c \cos A + a \cos C$

• Centroid, Incentre, and Circumcentre Coordinates

  • Centroid: $G = \left(\dfrac{x_1+x_2+x_3}{3}, \dfrac{y_1+y_2+y_3}{3}\right)$

  • Incentre: $I = \left(\dfrac{ax_1+bx_2+cx_3}{a+b+c}, \dfrac{ay_1+by_2+cy_3}{a+b+c}\right)$

  • Circumcentre: Located at the intersection of perpendicular bisectors of sides.

• Equation of Median and Altitude

  • Median: Line joining a vertex with the midpoint of the opposite side.

  • Altitude: Derived using the perpendicular slope condition from a vertex to the opposite side.

Some Special Formulae

We have provided below few important formulae which can help students in solving various mathematical problems.

Radius of Incircle

Inradius $r$ is given by:

$r = \dfrac{\Delta}{s}$

Alternative formulas:

$r = (s-a)\tan\dfrac{A}{2} = (s-b)\tan\dfrac{B}{2} = (s-c)\tan\dfrac{C}{2}$

Relation with circumradius $R$:

$r = 4R \sin\dfrac{A}{2}\sin\dfrac{B}{2}\sin\dfrac{C}{2}$

Exradii of a Triangle

In terms of area $\Delta$:

$r_1 = \frac{\Delta}{s-a}, \quad r_2 = \frac{\Delta}{s-b}, \quad r_3 = \frac{\Delta}{s-c}$

Using semi-perimeter $s$:

$r_1 = s \tan\frac{A}{2}, \quad r_2 = s \tan\frac{B}{2}, \quad r_3 = s \tan\frac{C}{2}$

In terms of circumradius $R$:

$\begin{aligned} r_1 &= 4R \sin\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2} \\ r_2 &= 4R \cos\frac{A}{2}\sin\frac{B}{2}\cos\frac{C}{2} \\ r_3 &= 4R \cos\frac{A}{2}\cos\frac{B}{2}\sin\frac{C}{2} \end{aligned}$

Distances of Special Points

Circumcentre ($O$):

$OA = R, \quad O_a = R\cos A$

Incentre ($I$):

$IA = r \csc\frac{A}{2}, \quad I_a = r$

Excentre ($I_1$):

$I_1A = r_1 \csc\frac{A}{2}$

Orthocentre ($H$):

$HA = 2R\cos A, \quad H_a = 2R \cos B \cos C$

Circumcenter and orthocentre:

$OH^2 = R^2 \big(1 - 8\cos A \cos B \cos C \big)$

Circumcentre and incentre: $OI^2 = R^2 \big(1 - 8\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}\big) = R^2 - 2Rr$

Orthocentre and Pedal Triangle

The Pedal Triangle is formed by joining the feet of the altitudes.

Angles: $\pi - 2A, \quad \pi - 2B, \quad \pi - 2C$

Sides: $a\cos A = R \sin 2A, \quad a\cos B = R \sin 2B, \quad a\cos C = R \sin 2C$

Circumradii of $\triangle PBC, \triangle PCA, \triangle PAB,$ and $\triangle ABC$ are equal.

Excentral Triangle

The triangle formed by joining the excentres $I_1, I_2, I_3$ is called the Excentral Triangle.

$\triangle ABC$ is the pedal triangle of $\triangle I_1I_2I_3$.

Angles: $\frac{\pi}{2} - \frac{A}{2}, \quad \frac{\pi}{2} - \frac{B}{2}, \quad \frac{\pi}{2} - \frac{C}{2}$

Sides: $4R\cos\frac{A}{2}, \quad 4R\cos\frac{B}{2}, \quad 4R\cos\frac{C}{2}$

Distances from incentre $I$: $II_1 = 4R\sin\frac{A}{2}, \quad II_2 = 4R\sin\frac{B}{2}, \quad II_3 = 4R\sin\frac{C}{2}$

The incentre $I$ of $\triangle ABC$ is the orthocentre of $\triangle I_1I_2I_3$.

M–n Rule

If $D$ lies on $BC$ dividing it in ratio $m:n$ ($BD:DC = m:n$), then:

$(m+n)\cot\theta = m\cot\alpha - n\cot\beta = n\cot B - m\cot C$

Apollonius’ Theorem

If $AD$ is a median through $A$:

$AB^2 + AC^2 = 2(AD^2 + BD^2)$

Length of Angle Bisectors, Medians, and Altitudes

Angle Bisector (from $A$):

$\beta_a = \frac{2bc \cos \tfrac{A}{2}}{b+c}$

Median (from $A$):

$m_a = \tfrac{1}{2}\sqrt{2b^2 + 2c^2 - a^2}$

Altitude (from $A$):

$A_a = \frac{2\Delta}{a}$

Solved Examples Based on Important Solutions of Triangle Formulas

Example 1: In triangle ABC , if $\mathrm{a}=2, \mathrm{~b}=1$ and $\angle C=60^{\circ}$ then find the other two angles.

Solution:

$\cos C = \frac{a^2 + b^2 - c^2}{2ab}$

$\tfrac{1}{2} = \frac{4 + 1 - c^2}{4}$

$c = \sqrt{3}$

Also, $\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$

$\frac{\sin A}{2} = \frac{\sin B}{1} = \frac{\tfrac{\sqrt{3}}{2}}{\sqrt{3}}$

$\sin A = 1 \;\Rightarrow\; A = \tfrac{\pi}{2}$

$\sin B = \tfrac{1}{2} \;\Rightarrow\; B = \tfrac{\pi}{6}$

Hence, the other two angles are $\tfrac{\pi}{6}, \tfrac{\pi}{2}$.

Example 2: Consider a triangle with sides $3^{\prime \prime}, 6^{\prime \prime}$ and $9^{\prime \prime}$. Find the $\angle A$.
Solution:

The triangle with sides $3^{\prime\prime}, 6^{\prime\prime}, 9^{\prime\prime}$.

Using the law of cosines:

$\cos A = \frac{b^2 + c^2 - a^2}{2bc}$

$\cos A = \frac{36 + 81 - 9}{108}$

$\cos A = 1$

$A = 0^{\circ}$

Hence, the answer is $0^{\circ}$.

Example 3: Consider a triangle with sides $5^{\prime \prime}, 8^{\prime \prime}$ and $10^{\prime \prime}$. Find the $\angle A, \angle B$, and $\angle C$.
Solution:

Given that, the triangle with sides $5^{\prime\prime}, 8^{\prime\prime}, 10^{\prime\prime}$.

Using the law of cosines:

$\cos A = \frac{b^2 + c^2 - a^2}{2bc}$

$\cos A = \frac{64 + 100 - 25}{160}$

$\cos A = 0.7125$

$A = 44.5^{\circ}$

Using the law of sines to find $\angle B$:

$\frac{\sin B}{b} = \frac{\sin A}{a}$

$\sin B = \frac{b}{a} \sin A$

$\sin B = \frac{8}{5} \sin 44.5^{\circ}$

$\sin B = \frac{8}{5} \times 0.7$

$\sin B = 1.12$

$B \approx 90^{\circ}$

The third angle is:

$C = 180^{\circ} - A - B$

$C = 45.4^{\circ}$

Hence, the answer is $45.4^{\circ}$.
Example 4: Two angles of a triangle are $45^\circ$ and $90^\circ$ and the side opposite the first angle is $35$ , find the side opposite the latter angle.

Solution: Given that,

Two angles of a triangle are $45^\circ$ and $90^\circ$

The side opposite the first angle is $35$

Using the sine formula,

$\frac{a}{\sin A} = \frac{b}{\sin B}$

$\frac{35}{\sin 45^\circ} = \frac{b}{\sin 90^\circ}$

$b = \frac{35}{\tfrac{1}{\sqrt{2}}}$

$b = 35\sqrt{2}$
Example 5: The area of the circle in which a chord of length $\sqrt{2}$ makes an angle $\pi / 2$ at the center is
Solution: Let AB be the chord of length, O be the center of the circle, and let OC be the perpendicular from O on AB .
Then $\mathrm{AC}=\mathrm{BC}=\sqrt{2} / 2=1 / \sqrt{2}$

In $\triangle O B C, \mathrm{OB}=\mathrm{BC} \operatorname{cosec} 450=(1 / \sqrt{2}) \times \sqrt{2}=1$

Area of the circle $=\pi(\mathrm{OB})^2=\pi$
Hence, the answer is $\pi$

List of Topics Related to the Important Solutions of triangle formulas

Explore the complete list of topics connected to triangle formulas, covering key concepts, theorems, and properties that are essential for competitive exams and board-level preparation.

NCERT Resources

Access NCERT Class 11 Maths study materials for Chapter 3 – Trigonometric Functions, including notes, solutions, and exemplar problems for effective exam preparation.

NCERT Class 11 Maths Notes for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Solutions for Chapter 3- Trigonometric Functions

NCERT Class 11 Maths Exemplar Solutions for Chapter 3- Trigonometric Functions

Practice Questions based on Important Solutions of triangle formulas

Solve triangle formula questions to strengthen concepts like area, perimeter, inradius, circumradius, and trigonometric rules for exam preparation.

Important Solutions Of Triangle Formulas - Practice Question MCQ

You can practice the related questions from the links shared below: