Trigonometric Functions
Starting from trigonometric functions class 10 to trigonometric functions class 12, these functions help calculate lengths, angles, and even arcs of circles. Understanding the domain and range of trigonometric functions, their formulas, derivatives, integration, and graphs of trigonometric functions is essential for solving problems in mathematics, physics, and engineering. In this article, you will find clear explanations of trigonometric functions formulas, derivatives of trigonometric functions, differentiation of inverse trigonometric functions, values of trigonometric functions, and ready-to-use trigonometric functions tables to make learning easier.
Origin of Trigonometry
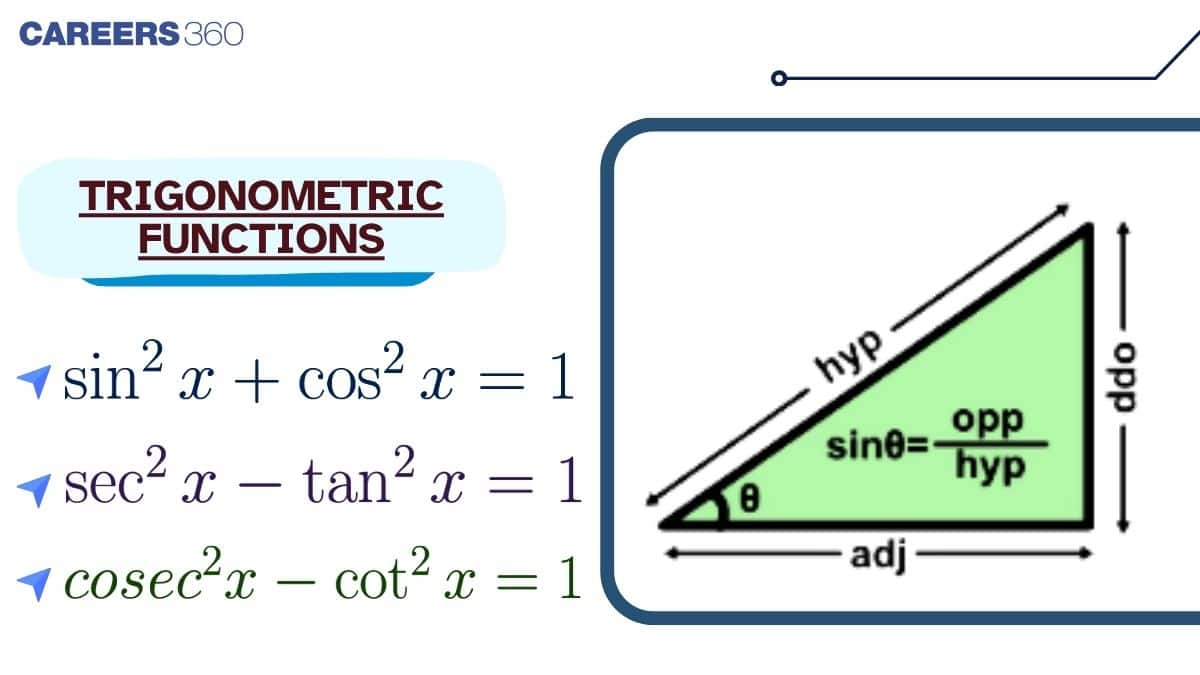
Trigonometry, in its simplest form, is the study of triangles with angles and lengths on their sides. When we break down the word trigonometry, we find that 'Tri' is a Greek word that means three,' 'Gon' means length,' and metry' means trigonometric formulas measurement.'
What are Trigonometric Functions?
In trigonometry, there are six basic trigonometric functions. These functions are trigonometric ratios that are based on ratios of sides in a right triangle: the hypotenuse (the longest side), the base (the side adjacent to a chosen angle), and the perpendicular (the side opposite the chosen angle). These functions are sine, cosine, tangent, secant, cosecant, and cotangent. They help us find different values in triangles by comparing these side lengths.

Trigonometric Functions Formulas
The trigonometric functions formulas are
1. Sine ($\sin$)- $\sin$ is defined as a ratio of the side opposite to that angle (perpendicular) and hypotenuse.
$\sin t=\frac{\text { opposite }}{\text { hypotenuse }}$
2. Cosine ($\cos$) - $\cos$ is defined as the ratio of the side adjacent to that angle (base) and hypotenuse.
$\cos t=\frac{\text { adjacent }}{\text { hypotenuse }}$
3. Tangent ($\tan$) - $\tan$ is defined as the ratio of the side opposite to that angle (perpendicular) and the side adjacent to that angle (base).
$\tan t=\frac{\text { opposite }}{\text { adjacent }}$
4. cotangent ($\cot$) - $\cot$ is defined as the ratio of the side adjacent to that angle (base) and the side opposite to that angle (perpendicular). It is the reciprocal of tan.
$\cot t=\frac{\text { adjacent }}{\text { opposite }}$
5. secant ($\sec$) - $\sec$ is defined as the ratio of the hypotenuse and the side adjacent to that angle (base). It is reciprocal of cos.
$\sec t=\frac{\text {hypotenuse }}{\text { adjacent }}$
6. Cosecant ($\csc$) - $\csc$ is defined as the ratio of the hypotenuse and the side opposite to that angle (perpendicular). It is reciprocal of the sin.
$\csc t=\frac{\text { hypotenuse }}{\text { opposite }}$
Values of Trigonometric Functions
In the trigonometric funcitons table, we use the values of trigonometric ratios for standard angles $0°, 30°, 45°, 60°,$ and $90º$. It is easy to use the table as a reference to calculate values of trigonometric ratios for various other angles, using the trigonometric ratio formulas for existing patterns within trigonometric ratios and even between angles.
Below are the trigonometric ratios of some special angles $0°, 30°, 45°, 60°,$ and $90º$

Domain and Range of Trigonometric Functions
Understanding the domain and range of trigonometric functions is essential for solving problems in mathematics, physics, and engineering. The domain of a function is the set of all input values (usually $x$) for which the function is defined, while the range is the set of all possible output values (usually $y$).
Domain and Range of Basic Trigonometric Functions
| Function | Domain | Range | Remarks / Special Cases |
|---|---|---|---|
| $\sin x$ | $(-\infty, \infty)$ | $[-1, 1]$ | Defined for all real numbers |
| $\cos x$ | $(-\infty, \infty)$ | $[-1, 1]$ | Defined for all real numbers |
| $\tan x$ | $x \neq \frac{\pi}{2} + n\pi, n \in \mathbb{Z}$ | $(-\infty, \infty)$ | Undefined where $\cos x = 0$ |
| $\cot x$ | $x \neq n\pi, n \in \mathbb{Z}$ | $(-\infty, \infty)$ | Undefined where $\sin x = 0$ |
| $\sec x$ | $x \neq \frac{\pi}{2} + n\pi, n \in \mathbb{Z}$ | $(-\infty, -1] \cup [1, \infty)$ | Reciprocal of $\cos x$ |
| $\csc x$ | $x \neq n\pi, n \in \mathbb{Z}$ | $(-\infty, -1] \cup [1, \infty)$ | Reciprocal of $\sin x$ |
Special Cases and Restrictions:
Functions like $\tan x$ and $\sec x$ are undefined wherever $\cos x = 0$.
Functions like $\cot x$ and $\csc x$ are undefined wherever $\sin x = 0$.
The range of $\sin x$ and $\cos x$ is always between -1 and 1.
Knowing these domains and ranges is crucial before applying derivatives of trigonometric functions or solving equations involving trigonometric identities.
This knowledge also helps in plotting the graph of trigonometric functions and understanding their behavior in different intervals.
Graph of Trigonometric Functions
The graph of trigonometric functions are
Sine ($\sin$)
$y = f(x) = \sin x$

Domain is $R$
Range is $[-1,1]$
We observe that $\sin x$ completes one full cycle of its possible values (from $-1$ to $1$ )
in the interval of length $2 \pi$.
So, the period of $\sin x$ is $2 \pi$.
The graph drawn in the interval $[0,2 \pi]$ repeats to the right and the left.
$\operatorname{Sin} x$ passes the graph as $\sin x=0$
So, The root of $y=\sin x$ is $n \pi$ where
$
n=\ldots \ldots-3,-2,-1,0,1,2,3,4 \ldots \ldots
$
Min value of $\sin x=-1$ at $=3 \pi / 2$
The max value of $\sin x=1$ at $\pi / 2$
Amplitude $=1$
$
\sin (-x)=-\sin x
$
So, $\sin \mathrm{x}$ is an odd function.
Cosine ($\cos$)
$y = f(x) = \cos x$

$
\sin (x+90)=\cos x
$
So, the $\cos x$ graph is drawn by shifting the $\sin \mathrm{x}$ graph by $90$ degrees.
Domain is $R$
Range is $[-1,1] \cos x=\pi / 2$. So, The root of $y=\cos x$ is $n(\pi / 2)$ where
$
n=\ldots \ldots-3,-2,-1,1,2,3,4 \ldots \ldots
$
Min value of $\cos x=-1$ at $2 \pi$
The max value of $\cos x=1$ at $0$ and $4 \pi$
Amplitude $=1$
Line of Symmetry $=\mathrm{Y}$ - axis
$
\cos (-x)=\cos x
$
So, $\cos x$ is an even function
Tangent ($\tan$)
$y=f(x) = \tan x$

Domain is $\mathbb{R}-\left\{\frac{(2 \mathrm{n}+1) \pi}{2}, \mathrm{n} \in \mathbb{I}\right\}$
Range is $R$
We observe that $\tan x$ increase in each of the intervals $\ldots$ $(-3 \pi / 2,-\pi / 2),(-\pi / 2, \pi / 2),(\pi / 2,3 \pi / 2) \ldots \ldots$.
The graph goes from negative to positive infinity. Period $=180$ degree $=\pi$. The root of the function $y=\tan x$ is $n \pi$ where $\mathrm{n}=\ldots \ldots-3,-2,-1,1,2,3 \ldots \ldots$
The amplitude is undefined as the graph tends to infinity.
Line of symmetry $=$ origin
$
\tan (-x)=-\tan x
$
So, the tangent function is odd.
Cosecant($\csc$)
$ y= f(x) = \csc x$

Domain is $\mathrm{R}-\{\mathrm{n} \pi, \mathrm{n} \in \mathrm{I}$ (Integers) $\}$
Range is $R-(-1,1)$
As the curve repeats after an interval of $2 \pi$, the period of the cosecant function is $2 \pi$.
The amplitude of the graph of a cosecant function is undefined as the curve does not have a maximum or a minimum value and tends to infinity.
Line of symmetry= origin
Vertical asymptotes are $x=n \pi$
$
\operatorname{cosec}(-x)=-\operatorname{cosec} x
$
So, $\operatorname{cosec} x$ is an odd function.
Secant ($\sec$)
$y=f(x)= \sec x$

Domain is $\mathbb{R}-\left\{\frac{(2 \mathrm{n}+1) \pi}{2}, \mathbf{n} \in \mathbb{I}\right\}$
The range is $R-(-1,1)$
The amplitude of the graph of a secant function is undefined as the curve does not have a maximum or a minimum value and tends to infinity. As the curve repeats after an interval of $2 \pi$, the period of the sunction is $2 \pi$.
Line of Symmetry $=\mathrm{Y}$-axis
Vertical asymptotes $=\mathrm{x}=(2 \mathrm{n}+1) \pi / 2$
$\operatorname{Sec}(-x)=\sec x$
So, it is an even function
Cotangent ($\cot$)
$y=f(x)= \cot x$

Domain is $\mathrm{R}-\{\mathrm{n} \pi, \mathrm{n} \in \mathrm{I}$ (Integers) $\}$
Range is $R$
The graph goes from negative to positive infinity.nWe observe that $\cot x$ decreases in each of the intervals $\ldots(-2 \pi /,-\pi),(-\pi, 0),(0, \pi) \quad$
The root of the equation $y=\cot x$ is $n \pi / 2$ where $n=\quad-3,-2,-1,1,2,3 . \quad$
The amplitude is undefined as the graph tends to infinity.
As the curve repeats after an interval of $\pi$, the period of the cotangent function is $\pi$. Line of symmetry $=$ origin
Vertical asymptotes are $x=n \pi$.
$\cot (-x)=-\cot x$
So it is an odd function.
Trigonometric Functions Identities
In trigonometry, identities help solve a variety of problems efficiently. These formulas are essential for tackling complex questions and provide fundamental resources for quick solutions. Below are the main trigonometric identities:
1. Pythagorean Identities
Trigonometric identities based on Pythagoras’ theorem:
$ \sin^2 t + \cos^2 t = 1 $
$ 1 + \tan^2 t = \sec^2 t $
$ 1 + \cot^2 t = \csc^2 t $
$ \tan t = \frac{\sin t}{\cos t}, \quad \cot t = \frac{\cos t}{\sin t} $
2. Reciprocal Identities
$ \csc t = \frac{1}{\sin t} $
$ \sec t = \frac{1}{\cos t} $
$ \cot t = \frac{1}{\tan t} $
3. Addition of Angles Identities
For two angles $A$ and $B$:
$ \sin(A+B) = \sin A \cos B + \cos A \sin B $
$ \cos(A+B) = \cos A \cos B - \sin A \sin B $
$ \tan(A+B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} $
4. Difference of Angles Identities
$ \sin(A-B) = \sin A \cos B - \cos A \sin B $
$ \cos(A-B) = \cos A \cos B + \sin A \sin B $
$ \tan(A-B) = \frac{\tan A - \tan B}{1 + \tan A \tan B} $
5. Double Angle Identities
$ \sin 2A = 2 \sin A \cos A $
$ \cos 2A = \cos^2 A - \sin^2 A = 2 \cos^2 A - 1 = 1 - 2 \sin^2 A $
$ \tan 2A = \frac{2 \tan A}{1 - \tan^2 A} $
6. Identities of Allied Angles
$ \sin(90-\theta) = \cos \theta, \quad \cos(90-\theta) = \sin \theta $
$ \tan(90-\theta) = \cot \theta, \quad \cot(90-\theta) = \tan \theta $
$ \sec(90-\theta) = \csc \theta, \quad \csc(90-\theta) = \sec \theta $
$ \sin(90+\theta) = \cos \theta, \quad \cos(90+\theta) = -\sin \theta $
$ \tan(90+\theta) = -\cot \theta, \quad \cot(90+\theta) = -\tan \theta $
$ \sec(90+\theta) = -\csc \theta, \quad \csc(90+\theta) = \sec \theta $
7. Triple Angle Identities
$ \sin 3A = 3 \sin A - 4 \sin^3 A $
$ \cos 3A = 4 \cos^3 A - 3 \cos A $
$ \tan 3A = \frac{3 \tan A - \tan^3 A}{1 - 3 \tan^2 A} $
$ \cot 3A = \frac{\cot^3 A - 3 \cot A}{3 \cot^2 A - 1} $
8. Supplementary Angle Identities
$ \sin(180-\theta) = \sin \theta, \quad \cos(180-\theta) = -\cos \theta $
$ \tan(180-\theta) = -\tan \theta, \quad \cot(180-\theta) = -\cot \theta $
$ \sec(180-\theta) = -\sec \theta, \quad \csc(180-\theta) = \csc \theta $
9. Sum-Product Identities
$ \sin C + \sin D = 2 \sin \frac{C+D}{2} \cos \frac{C-D}{2} $
$ \sin C - \sin D = 2 \cos \frac{C+D}{2} \sin \frac{C-D}{2} $
$ \cos C + \cos D = 2 \cos \frac{C+D}{2} \cos \frac{C-D}{2} $
$ \cos C - \cos D = -2 \sin \frac{C+D}{2} \sin \frac{C-D}{2} $
10. Identities of Opposite Angles
$ \sin(-A) = -\sin A, \quad \cos(-A) = \cos A $
$ \tan(-A) = -\tan A, \quad \cot(-A) = -\cot A $
$ \sec(-A) = \sec A, \quad \csc(-A) = -\csc A $
Inverse Trigonometric Functions
Inverse trigonometric functions “undo” the action of the original trigonometric functions. In other words, the domain of the inverse function is the range of the original function, and the range of the inverse function is the domain of the original function.
For example, if $f(x) = \sin x$, then its inverse is written as $f^{-1}(x) = \sin^{-1} x$. Note that $\sin^{-1} x$ is not the same as $\frac{1}{\sin x}$.
Examples of Inverse Trigonometric Functions
$ \sin(\pi/6) = 1/2 \implies \pi/6 = \sin^{-1}(1/2) $
$ \cos(\pi) = -1 \implies \pi = \cos^{-1}(-1) $
$ \tan(\pi/4) = 1 \implies \pi/4 = \tan^{-1}(1) $
Domain and Range of Inverse Trigonometric Functions
| Function | Domain | Range |
|---|---|---|
| $y = \sin^{-1} x$ | $[-1, 1]$ | $[-\pi/2, \pi/2]$ |
| $y = \cos^{-1} x$ | $[-1, 1]$ | $[0, \pi]$ |
| $y = \tan^{-1} x$ | $\mathbb{R}$ | $(-\pi/2, \pi/2)$ |
| $y = \cot^{-1} x$ | $\mathbb{R}$ | $(0, \pi)$ |
| $y = \sec^{-1} x$ | $(-\infty, -1] \cup [1, \infty)$ | $[0, \pi] - {\pi/2}$ |
| $y = \csc^{-1} x$ | $(-\infty, -1] \cup [1, \infty)$ | $[-\pi/2, \pi/2] - {0}$ |
Differentiation of Trigonometric Functions
The derivative of a trigonometric function gives the slope of the tangent to its curve. These formulas are essential for finding tangents, normals, or solving calculus problems.
$ \frac{d}{dx}(\sin x) = \cos x $
$ \frac{d}{dx}(\cos x) = -\sin x $
$ \frac{d}{dx}(\tan x) = \sec^2 x $
$ \frac{d}{dx}(\cot x) = -\csc^2 x $
$ \frac{d}{dx}(\sec x) = \sec x \tan x $
$ \frac{d}{dx}(\csc x) = -\csc x \cot x $
Integration of Trigonometric Functions
Integration is used to calculate areas under curves of trigonometric functions or areas of irregular plane surfaces.
$ \int \sin x , dx = -\cos x + C $
$ \int \cos x , dx = \sin x + C $
$ \int \tan x , dx = \log |\sec x| + C $
$ \int \cot x , dx = \log |\sin x| + C $
$ \int \sec^2 x , dx = \tan x + C $
$ \int \csc^2 x , dx = -\cot x + C $
$ \int \sec x \tan x , dx = \sec x + C $
$ \int \csc x \cot x , dx = -\csc x + C $
$ \int \sec x , dx = \log |\sec x + \tan x| + C $
$ \int \csc x , dx = \log |\csc x - \cot x| + C $
Solved Examples based on Trigonometric Functions
Solution: Given: $4 \sec A + 5 = 0$
$\Rightarrow \sec A = -\dfrac{5}{4}$
Since $ABCD$ is a convex quadrilateral, angle $A$ lies between $\dfrac{\pi}{2}$ and $\pi$ (i.e., second quadrant), where:
$\cos A < 0$
$\sin A > 0$
$\tan A < 0$
Now, $\sec A = \dfrac{1}{\cos A} = -\dfrac{5}{4}$
$\Rightarrow \cos A = -\dfrac{4}{5}$
Using identity: $\sin^2 A + \cos^2 A = 1$
$\Rightarrow \sin^2 A = 1 - \left(-\dfrac{4}{5}\right)^2 = 1 - \dfrac{16}{25} = \dfrac{9}{25}$
$\Rightarrow \sin A = \dfrac{3}{5}$ (positive in second quadrant)
Now, $\tan A = \dfrac{\sin A}{\cos A} = \dfrac{\dfrac{3}{5}}{-\dfrac{4}{5}} = -\dfrac{3}{4}$
$cosec A = \dfrac{1}{\sin A} = \dfrac{5}{3}$
Now, let the quadratic equation with roots $\tan A$ and $cosec A$ be:
$(x - \tan A)(x - cosec A) = 0$
Substitute values: $\left(x + \dfrac{3}{4}\right)\left(x - \dfrac{5}{3}\right) = 0$
Multiply: $x^2 - \dfrac{5}{3}x + \dfrac{3}{4}x - \dfrac{15}{12} = 0$
Combine terms: $x^2 - \left(\dfrac{5}{3} - \dfrac{3}{4}\right)x - \dfrac{15}{12} = 0$
$\Rightarrow x^2 - \dfrac{11}{12}x - \dfrac{15}{12} = 0$
Multiply throughout by 12 to remove denominators:
$12x^2 - 11x - 15 = 0$
Example 2: What is the range of $f(x)=\sin|3x^3| \ \ x\epsilon R$?
Solution: Graph of sine function
y = f(x) = sin(x)
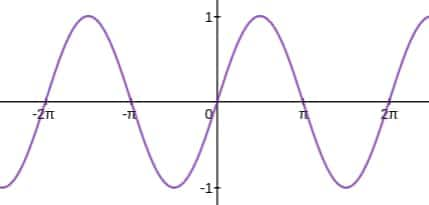
Now,
$f(x)=\sin \left|3 x^3\right|, \quad x \in R$
$\text { assume }\left|3 x^3\right|=t, \quad t \geq 0$
Now, from graph if $t \geq 0$, then $y=\sin (t)$ takes all values in $[-1,1]$ So, range is $[-1,1]$.
Example 3: The number of solutions of $\sin 3x = \cos 2x$, in the interval $\left(\frac{\pi}{2}, \pi\right)$ is: [JEE MAINS 2018]
Solution: We are given the equation: $\sin 3x = \cos 2x$
Using the identity: $\cos \theta = \sin\left(\frac{\pi}{2} - \theta\right)$
We rewrite the equation as: $\sin 3x = \sin\left(\frac{\pi}{2} - 2x\right)$
Now using the identity: If $\sin A = \sin B$, then
$A = B + 2n\pi$ or $A = \pi - B + 2n\pi$
Case 1: $3x = \frac{\pi}{2} - 2x + 2n\pi$
$\Rightarrow 5x = \frac{\pi}{2} + 2n\pi$
$\Rightarrow x = \frac{\pi + 4n\pi}{10}$
Case 2: $3x = \pi - \left(\frac{\pi}{2} - 2x\right) + 2n\pi$
$\Rightarrow 3x = \frac{\pi}{2} + 2x + 2n\pi$
$\Rightarrow x = \frac{\pi}{2} + 2n\pi$
Now find values of $x$ in the interval $\left(\frac{\pi}{2}, \pi\right)$
From Case 1: $x = \frac{(1 + 4n)\pi}{10}$
Try $n = 1$: $x = \frac{5\pi}{10} = \frac{\pi}{2}$ excluded
Try $n = 2$: $x = \frac{9\pi}{10} \in \left(\frac{\pi}{2}, \pi\right)$
Try $n = 3$: $x = \frac{13\pi}{10} > \pi$ not allowed
From Case 2: $x = \frac{\pi}{2} + 2n\pi$ all values exceed $\pi$ in the interval
So, only one solution exists.
Hence, the number of solutions is $1$.
Example 4: The value of $\cos \frac{\pi}{19}+\cos \frac{3 \pi}{19}+\cos \frac{5 \pi}{19}+\ldots . .+\cos \frac{17 \pi}{19}$ is equal to (up to one decimal point):
1) $0.5$
2) $0$
3) $1$
4) $0.7$
Solution:
The trigonometric ratios for angles in all the four quadrants.
$
\begin{aligned}
& \cos \frac{\pi}{19}+\cos \frac{3 \pi}{19}+\cos \frac{5 \pi}{19}+\ldots .+\cos \frac{17 \pi}{19} \\
& \text { Here, } A=\frac{\pi}{19}, D=\frac{2 \pi}{19}, n=9 \\
& \because \cos A+\cos (A+D)+\cos (A+2 D)+\ldots \ldots . .+\cos (A+(n-1) D) \\
& =\frac{\sin \left(\frac{n D}{2}\right)}{\sin \frac{D}{2}} \cdot \cos \left(\frac{2 A+(n-1) D}{2}\right)=\frac{\sin 9 \times \frac{\pi}{19}}{\sin \frac{\pi}{19}} \times \cos \left(\frac{\frac{\pi}{19}+\frac{17 \pi}{19}}{2}\right) \\
& =\frac{\sin \frac{9 \pi}{19}}{\sin \frac{\pi}{19}} \times \cos \frac{9 \pi}{19} \\
& =\frac{1}{2} \cdot \frac{\sin \left(\frac{18 \pi}{19}\right)}{\sin \frac{\pi}{19}}=\frac{1}{2} \cdot \frac{\sin \frac{\pi}{19}}{\sin \frac{\pi}{19}}=\frac{1}{2}
\end{aligned}
$
Example 5: The value of the sum $\sum_{k=1}^n\left(\tan 2^{k-1} \cdot \sec 2^k\right)$ is
1) $\tan 2^n$
2) $\tan 2^n-1$
3) $\tan 2^n-\tan 1$
4) $\cos 2^n-\cos 2$
Solution:
$
\sum_{k=1}^n\left(\tan 2^{k-1} \cdot \sec 2^k\right)
$
$
\begin{aligned}
& \text { As } \sec \left(2.2^{k-1}\right)=\frac{1}{\cos \left(2.2^{k-1}\right)} \\
& =\sum_{k=1}^n \tan 2^{k-1} \times \frac{1+\tan ^2 2^{k-1}}{1-\tan ^2 2^{k-1}} \\
& =\sum_{k=1}^n\left(\frac{\tan (2)^{k-1}\left[2-1+\tan ^2 2^{k-1}\right]}{1-\tan ^2 2^{k-1}}\right) \\
& =\sum_{k=1}^n\left(\frac{2 \tan 2^{k-1}}{1-\tan ^2 2^{k-1}}-\tan (2)^{k-1}\right) \\
& =\sum_{k=1}^n\left(\tan 2^k-\tan 2^{k-1}\right) \\
& =\tan 2-\tan (1)+\tan 2^2-\tan 2+\ldots \tan 2^n-\tan 2^{n-1} \\
& =\tan 2^n-1
\end{aligned}
$
Hence, the answer is the option 3.
List of Topics related to Trigonometric Functions acoording to NCERT/JEE MAIN
This section provides a complete list of important trigonometric functions topics as per NCERT and JEE Main syllabus. It helps you focus on the right areas for formulas, graphs, derivatives, and integration. Following this list ensures that you don’t miss any key concept while preparing for exams.
NCERT Resources
This section offers you the important NCERT resources for Class 11 Chapter 3 – Trigonometric Functions. You'll get detailed notes, step-by-step NCERT solutions, and NCERT Exemplar problems, making it simple to master Trigonometric Ratios.
NCERT Class 11 Chapter 3 - Trigonometric Functions Notes
NCERT Class 11 Chapter 3 - Trigonometric Functions Solutions
NCERT Exemplar Class 11 Chapter 3 - Trigonometric Functions
Important Books for Trigonometric Functions
This section lists the best books for studying trigonometric functions, covering formulas, and graphs, etc. These books provide clear explanations and plenty of practice questions to strengthen your concepts and exam preparation.
| Book Title | Author / Publisher | Description |
|---|---|---|
| NCERT Mathematics Textbook (Class 11) | NCERT | Official textbook; covers the fundamentals of trigonometric functions in a clear, accessible way. Essential for exams and foundational concepts. |
| Trigonometry | S. L. Loney | A classic reference with deep explanations and a wide range of problems, perfect for additional practice and conceptual clarity. |
| Cengage Maths (Trigonometry volume) | Cengage Learning | Illustrative text and rigorous problem sets focusing on competitive exam preparation (JEE Main/Advanced). |
| RD Sharma Mathematics (Class 11 & 12) | RD Sharma | Contains topic-wise solved examples and exercises for building and reinforcing concepts. |
NCERT Subjectwise Resources
This section provides NCERT subjectwise resources for helping you study each topic for each subject clearly. It includes explanations, examples, and practice questions to build a strong foundation.
| Resource Type | Mathematics | Physics | Chemistry |
|---|---|---|---|
| NCERT Notes | NCERT notes Class 11 Maths | NCERT notes Class 11 Physics | NCERT notes Class 11 Chemistry |
| NCERT Solutions | NCERT solutions for Class 11 Mathematics | NCERT solutions for Class 11 Physics | NCERT solutions for Class 11 Chemistry |
Practice Questions based on Trigonometric Functions
This section offers practice questions on trigonometric functions to help you apply formulas, derivatives, and graphs. Solving these problems will improve your understanding and prepare you for exams like JEE Main.
Frequently Asked Questions (FAQs)
The six basic trigonometric functions are $\sin$, $\cos$, $\tan$, $\cot$, $\sec$, and $\csc$, which relate the sides of a right-angled triangle to its angles.
$\cos$ is positive in Quadrant I and Quadrant IV of the coordinate plane.
The value of $\sin 120° = \sin(180° - 60°) = \sin 60° = \sqrt{3}/2$.
Trigonometric functions class 11 covers the study of $\sin$, $\cos$, $\tan$, and other ratios, their properties, formulas, graphs, and applications in triangles.
Quadrant 4 is where x-values are positive and y-values are negative, so $\cos$ and $\sec$ are positive, while $\sin$, $\csc$, $\tan$, and $\cot$ are negative.
The 6 basic trigonometric functions are sine($\sin$), cosine($\cos$), tangent($\tan$), cosecant($\csc$), secant($\sec$) and cotangent($\cot$).