Trigonometric Ratios - Definition, Formulas and Examples

Trigonometric Ratios are fundamental concepts in mathematics that describe the relationship between the angles and sides of a right-angled triangle. These ratios — Sine, Cosine, and Tangent — are widely used in geometry, physics, engineering, and competitive exams like JEE and NEET. Understanding Trigonometric Ratios in a Right-Angled Triangle helps students solve problems related to heights, distances, and angles effectively. In this article, we’ll explore the Trigonometric Ratios Formula, their values for standard angles, the Trigonometric Ratios Table, and the Relation Between Trigonometric Ratios.

This Story also Contains

1. What Are Trigonometric Ratios?
2. Understanding the Trigonometric Ratios – Sine, Cosine, and Tangent
3. Trigonometric Ratios Formula
4. Trigonometric Ratios Table for Standard Angles
5. Relation between trigonometric Ratios
6. Application of Trigonometric Ratios in Height and Distance:
7. Importance of Trigonometric Ratios in Mathematics and Real Life
8. List of Topics Related to the Trigonometric Ratios
9. NCERT Resources
10. Practice Questions

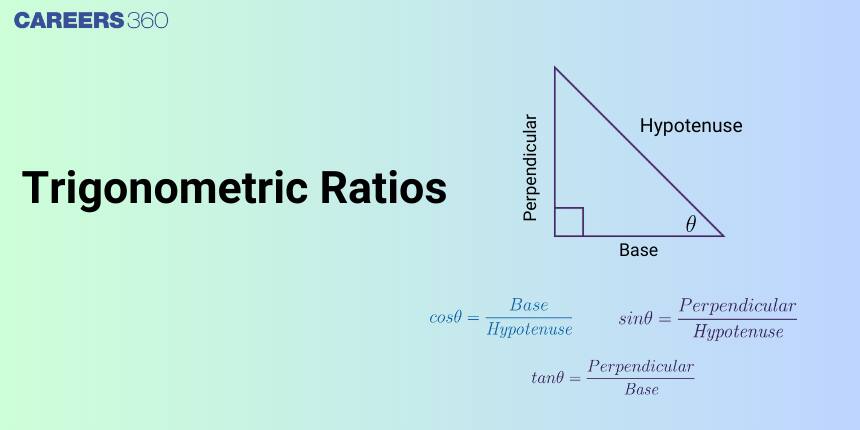
What Are Trigonometric Ratios?

In trigonometry, trigonometric ratios are used to establish a relationship between the angles and sides of a right-angled triangle. These ratios are the foundation for solving a wide range of geometric and real-world problems. In this section, we will define the trigonometric ratios, understand their significance in a right-angled triangle, and explore their importance in mathematics and daily life.

Definition of Trigonometric Ratios in a Right-Angled Triangle

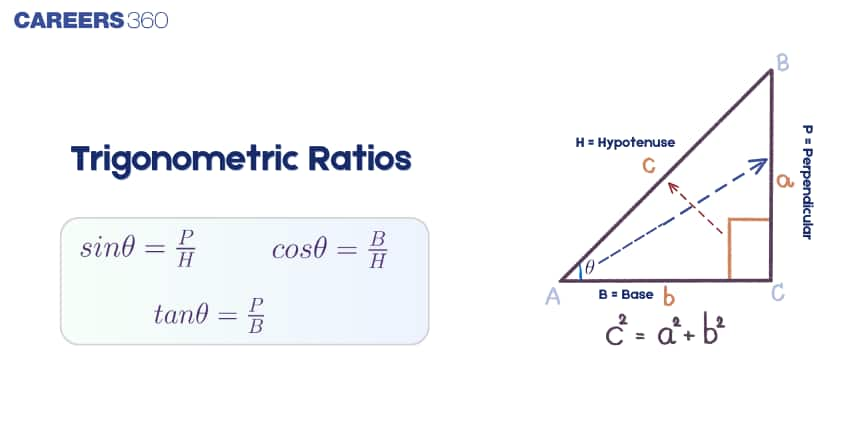
Trigonometric ratios are defined for an acute angle of a right-angled triangle as the ratios between different pairs of its sides. The primary trigonometric ratios are:

• Sine, written as $\sin$
• Cosine, written as $\cos$
• Tangent, written as $\tan$

Let $\theta$ be an acute angle in a right-angled triangle. Then:

$\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse}}, \quad \cos \theta = \frac{\text{Adjacent side}}{\text{Hypotenuse}}, \quad \tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}}$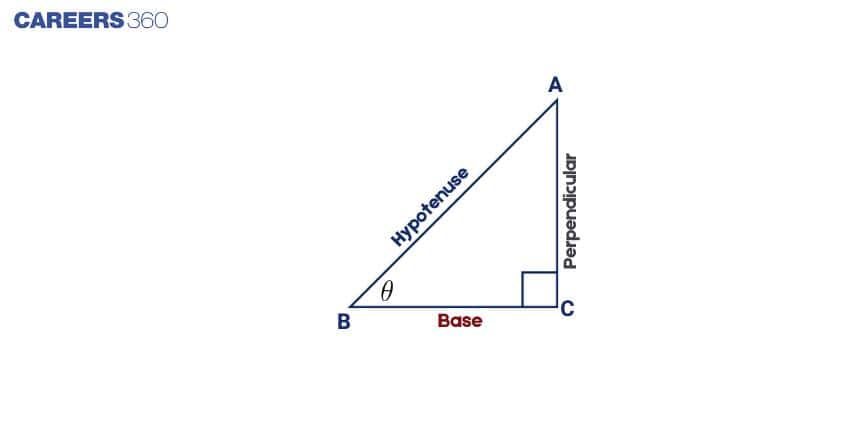

In addition to these, we have the reciprocal trigonometric ratios:

$\csc \theta = \frac{1}{\sin \theta}, \quad \sec \theta = \frac{1}{\cos \theta}, \quad \cot \theta = \frac{1}{\tan \theta}$

Example:

Consider a right-angled triangle where $\theta = 30^\circ$, the opposite side is 1 unit, and the hypotenuse is 2 units. Using the definitions:

$\sin 30^\circ = \frac{1}{2}, \quad \cos 30^\circ = \frac{\sqrt{3}}{2}, \quad \tan 30^\circ = \frac{1}{\sqrt{3}}$

These values are part of the Trigonometric Ratios Table of Standard Angles, which you will learn about in a later section.

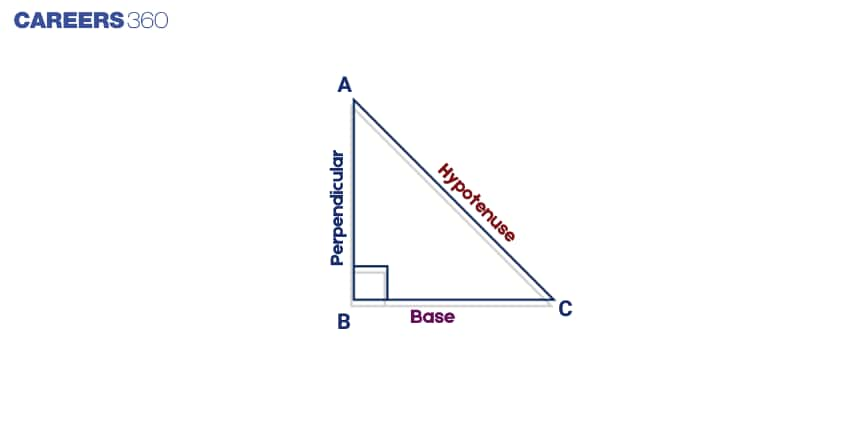
Sides and angles of a Right angled Triangle

The right angle triangle is a triangle in which one angle is 90 degrees.

Consider the triangle ABC, given above.

Base: If we wish to take trigonometric ratios of angle B, then the base is BC. It is the side on which the right-angle triangle stands.

Perpendicular (Altitude): Side opposite to the angle for which we want to find the trigonometric ratio.
In this case, AB is the altitude.
BC and AB are perpendicular to each other.

Hypotenuse: The side opposite to the right angle is called the hypotenuse. It is the largest side of the triangle. Side AC is the hypotenuse.

Understanding the Trigonometric Ratios – Sine, Cosine, and Tangent

In this section, we’ll dive deeper into the core trigonometric ratios: sine, cosine, and tangent. You'll understand their meaning, how they're derived from right-angled triangles, how to remember them easily, and how to apply them through examples.

Sine, Cosine, Tangent – Basic Meaning and Formula

The three most commonly used trigonometric ratios are sine ($\sin$), cosine ($\cos$), and tangent ($\tan$). These ratios are defined in a right-angled triangle based on an acute angle $\theta$:

$\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse}}, \quad \cos \theta = \frac{\text{Adjacent side}}{\text{Hypotenuse}}, \quad \tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}}$

These definitions apply only in a right-angled triangle, where one angle is exactly $90^\circ$.

Examples Using Sine, Cosine, and Tangent Ratios

Let’s apply the definitions with a practical example:

Example: In a triangle, angle $\theta = 60^\circ$, and the hypotenuse is 10 cm. Find the opposite side using $\sin \theta$.

$\sin 60^\circ = \frac{\text{Opposite}}{10} \Rightarrow \frac{\sqrt{3}}{2} = \frac{\text{Opposite}}{10}sin60∘=10Opposite⇒23=10Opposite Opposite side=10⋅32=53 cm\text{Opposite side} = 10 \cdot \frac{\sqrt{3}}{2} = 5\sqrt{3} \, \text{cm}$

This illustrates how trigonometric ratios can help determine unknown side lengths when an angle is known.

Trigonometric Ratios Formula

This section provides a complete collection of formulas related to Trigonometric Ratios, including reciprocal identities and the relations that exist among them. These formulas are crucial for solving higher-level problems in competitive exams like JEE, NEET, and school boards.

Basic Formulas of Trigonometric Ratios

The six trigonometric ratios are:

$\sin \theta = \frac{\text{Opposite}}{\text{Hypotenuse}}, \quad \cos \theta = \frac{\text{Adjacent}}{\text{Hypotenuse}}, \quad \tan \theta = \frac{\text{Opposite}}{\text{Adjacent}}$

Their reciprocals:

$\csc \theta = \frac{1}{\sin \theta}, \quad \sec \theta = \frac{1}{\cos \theta}, \quad \cot \theta = \frac{1}{\tan \theta}$

Reciprocal Identities: Secant, Cosecant, and Cotangent

These identities help express less common trigonometric ratios in terms of the primary ones:

$\csc \theta = \frac{1}{\sin \theta}, \quad \sec \theta = \frac{1}{\cos \theta}, \quad \cot \theta = \frac{1}{\tan \theta}$

These are particularly important when solving problems involving heights and distances or wave motion in physics.

Relation Between Trigonometric Ratios

Trigonometric ratios are closely interconnected. Some standard relations include:

$\tan \theta = \frac{\sin \theta}{\cos \theta}, \quad \cot \theta = \frac{\cos \theta}{\sin \theta}$

Pythagorean identities:

$\sin^2 \theta + \cos^2 \theta =1$

$1 + \tan^2 \theta = \sec^2 \theta$

$1 + \cot^2 \theta = \csc^2 \theta$

These identities are fundamental tools for simplifying complex trigonometric expressions.

Trigonometric Ratios Table for Standard Angles

This section contains the complete Trigonometric Ratios Table for standard angles $0^\circ$, $30^\circ$, $45^\circ$, $60^\circ$, and $90^\circ$. Mastering this table is essential for quick calculations in both school exams and competitive tests.

Easy Tricks to Memorize the Trigonometric Ratios Table

One popular method to remember $\sin \theta$ for standard angles:

$\sin \theta = \sqrt{\frac{n}{4}}, \quad \text{where } n = 0, 1, 2, 3, 4$

So for:

• $\sin 0^\circ = \sqrt{0/4} = 0$
• $\sin 30^\circ = \sqrt{1/4} = \frac{1}{2}$
• $\sin 45^\circ = \sqrt{2/4} = \frac{1}{\sqrt{2}}$
• $\sin 60^\circ = \sqrt{3/4} = \frac{\sqrt{3}}{2}$
• $\sin 90^\circ = \sqrt{4/4} = 1$
  

Use this to also derive $\cos \theta$ as:

$\cos \theta = \sin (90^\circ - \theta)$

This reverse relationship is especially useful for quick mental calculations.

We can use some of the famous mnemonics to remember the main three sinθ, cosθ, and tanθ.

For sinθ, we will remember “Some People Have” [S = sinθ, P = Perpendicular, H = Hypotenuse]

For cosθ, we will remember “Curly Black Hair” [C = cosθ, B = Base, H = Hypotenuse]

For tanθ, we will remember “Through Proper Brushing” [T = tanθ, P = Perpendicular, B = Base]

Relation between the sides of a right-angled triangle: Pythagoras's theorem

Statement:

The square of the hypotenuse is equal to the sum of the squares of the base and the square of the altitude.

$(Hypotenuse)^2= (Base)^2 + (Altitude)^2$

Pythagorean Triplets:

The three numbers which satisfy the above equation are known as the Pythagorean triplets.

For example, $(3, 4, 5)$ is a Pythagorean triplet because we know that $3^2= 9, 4^2 = 16$, and $5^2 = 25$ and, $9 + 16 = 25$.

Therefore, $3^2+4^2=5^2$.

Any three numbers that satisfy this condition are called Pythagorean triplets like $3, 4$, and $5$.

Some of the other examples of Pythagorean triplets are $(6, 8, 10)$, and $(12, 5, 13)$.

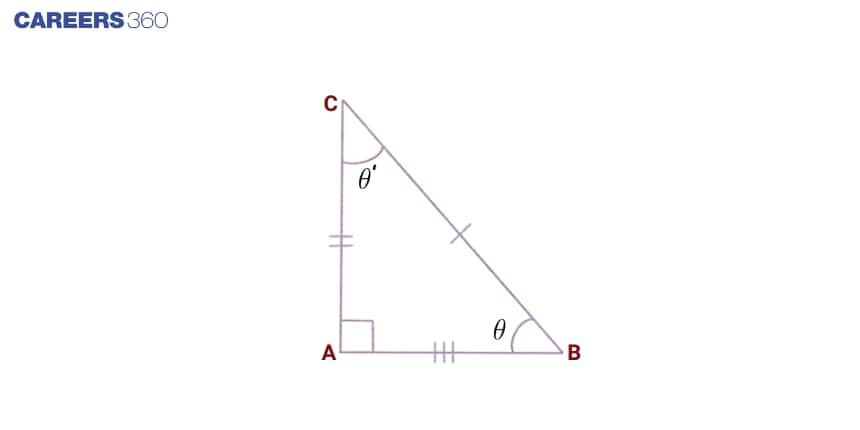
Sometimes choosing the perpendicular side can be tough. It depends on the angle.

In the above triangle ABC,

For $∠CBA$, $sin\theta = \frac{AC}{BC}$

i.e., Here $AC$ is the perpendicular.

For $∠ACB$, $sin\theta’ = \frac{AB}{BC}$,

i.e., Here $AB$ is the perpendicular.

For this, we have to remember the adjacent side and opposite side.

Perpendicular = Opposite side of the angle considered

Base = Adjacent side of the angle considered

Hypotenuse will be the same in every case.

Relation between trigonometric Ratios

As we observe that sinθ is a reciprocal of cosecθ, cosθ is a reciprocal of secθ, tanθ is a reciprocal of cotθ, and vice-versa.

So, we can say

$ \sin \theta = \frac{1}{\csc \theta} $

$ \cos \theta = \frac{1}{\sec \theta} $

$ \tan \theta = \frac{1}{\cot \theta} $

$ \csc \theta = \frac{1}{\sin \theta} $

$ \sec \theta = \frac{1}{\cos \theta} $

$ \cot \theta = \frac{1}{\tan \theta} $

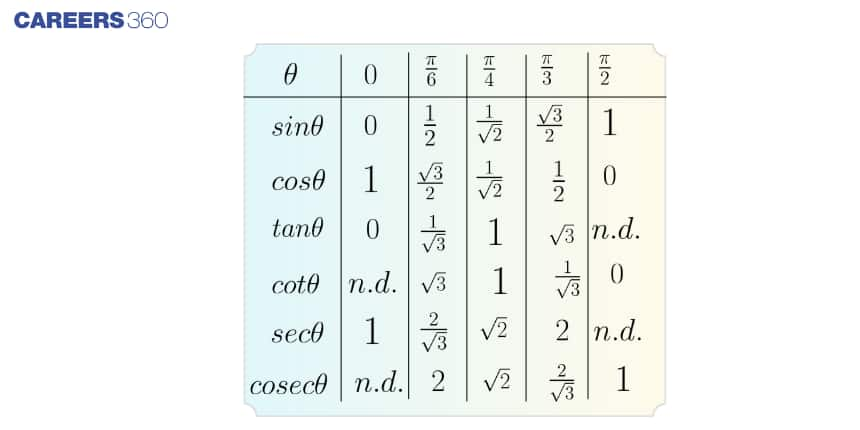
Trigonometric Ratio Table

Trigonometric Ratios of $0^\circ$, $30^\circ$, $45^\circ$, $60^\circ$, and $90^\circ$. The standard values of $\sin \theta$, $\cos \theta$, and $\tan \theta$ for the five commonly used angles are as follows:

Trigonometric Ratios for Complementary Angles

The complementary angles are a pair of two angles such that their sum is equal to 90°. The complement of an angle $\theta$ is $90° - \theta$. The trigonometric ratios of complementary angles are:

$\sin(90^\circ - \theta) = \cos \theta $

$ \cos(90^\circ - \theta) = \sin \theta $

$ \csc(90^\circ - \theta) = \sec \theta $

$ \sec(90^\circ - \theta) = \csc \theta $

$ \tan(90^\circ - \theta) = \cot \theta $

$ \cot(90^\circ - \theta) = \tan \theta$

We can see from above that sine and cosine are complementary to each other, cosecant and secant are complementary to each other, and tangent and cotangent are complementary to each other.

Application of Trigonometric Ratios in Height and Distance:

Trigonometry is one of the most important branches of mathematics. Some of the applications of trigonometry are:

• Measuring the heights of towers or big mountains
• Determining the distance of the shore from the sea
• Finding the distance between two celestial bodies
• Determining the power output of solar cell panels at different inclinations
• Representing different physical quantities such as mechanical waves, electromagnetic waves, etc.

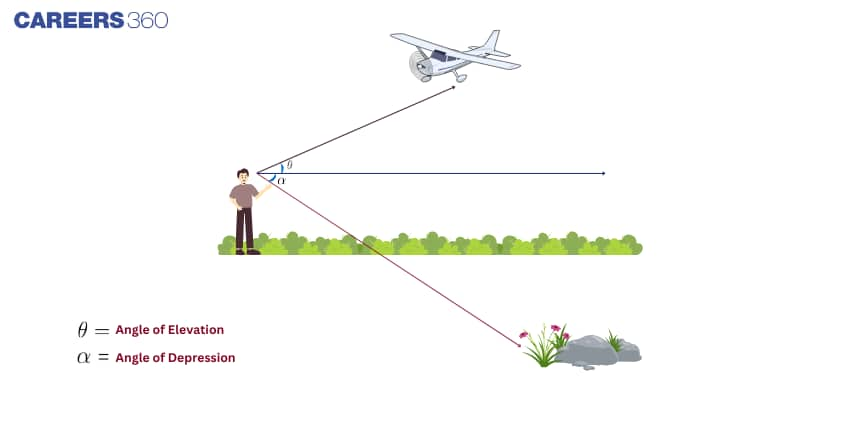
Angle of Elevation and Angle of Depression:

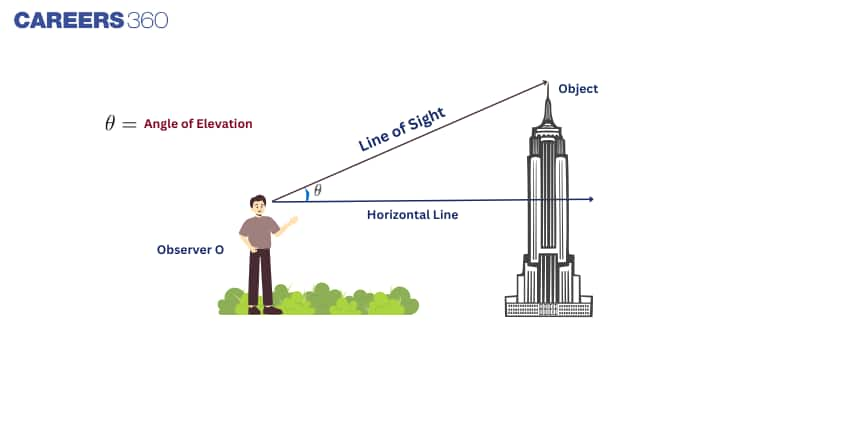
What is Angle of Elevation?

When you see an object above you, there's an angle between the horizontal and your line of sight to the object.

What is Angle of Depression?

When you see an object below you, there's an angle between the horizontal and your line of sight to the object.

Importance of Trigonometric Ratios in Mathematics and Real Life

Trigonometric ratios play a vital role in both academics and practical applications. Whether you're a student learning geometry or an engineer designing bridges, understanding these ratios is essential.

In Real Life and Applications:

• Engineering: Calculating slopes, angles, and lengths in design and construction
• Astronomy: Measuring distances between stars and planets using angular calculations
• Navigation: Determining directions, bearings, and locations using GPS technology
• Physics: Describing wave motion, oscillations, and circular motion

Example:

A surveyor standing 50 meters away from a tower observes its top at an angle of elevation of $60^\circ$. To find the height $h$ of the tower:

$\tan 60^\circ = \frac{h}{50} \Rightarrow h = 50 \cdot \sqrt{3} \approx 86.6 \, \text{meters}$

This example shows how tangent ratio is directly applied in solving height and distance problems, which are part of both academic and real-world scenarios.

Solved Examples

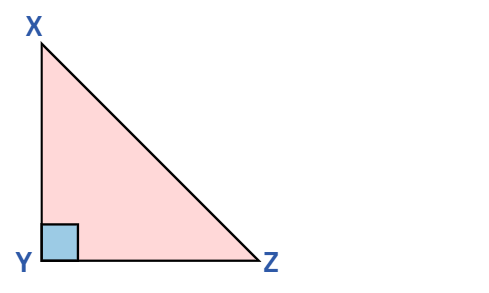
Q1. In $\triangle{XYZ}$, right-angled at $Y$, if $\sin X = \frac{1}{2}$, find the value of $\cos X \cos Z + \sin X \sin Z$.

1. $\frac{\sqrt{3}}{2}$
2. $\frac{\sqrt{3}}{4}$
3. $\frac{2}{\sqrt{3}}$
4. $\sqrt{3}$

Hint: The sum of all angles in a triangle is 180°. Use this to find the value of $\cos X \cos Z + \sin X \sin Z$.

Answer:

Given: In $\triangle {XYZ}$, right-angled at $Y$.

We know that the sum of all the angles in a triangle is 180°.

$\sin X = \frac{1}{2}$

⇒ $\sin X = \sin{30°}$

So, $\angle X = 30°$

Then $\angle Z = 60°$, because $\angle Y + \angle X + \angle Z = 180°$

Then, $\cos X \cos Z + \sin X \sin Z$

$=\cos 30° \cos 60° + \sin 30° \sin 60°$

$=\frac{\sqrt{3}}{2} × \frac{1}{2} + \frac{1}{2} × \frac{\sqrt{3}}{2}$

$ = \frac{\sqrt{3}}{2}$

Hence, the correct answer is $\frac{\sqrt{3}}{2}$.

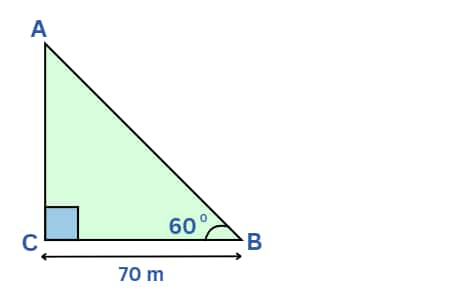
Q2. The angle of elevation of the top of a building at a distance of 70 m from its foot on a horizontal plane is found to be 60°. Find the height of the building.

1. $70 \sqrt{3} \mathrm{~m}$
2. $60 \sqrt{3} \mathrm{~m}$
3. $50 \sqrt{3} \mathrm{~m}$
4. $70 \sqrt{2} \mathrm{~m}$

Hint: Use formula, $\tan \theta=\frac{\text{Perpendicular}}{\text{Base}}$

Answer:

Height = AC

We know, $\tan \theta=\frac{\text{Perpendicular}}{\text{Base}}$

⇒ $\tan60° =\frac{AC}{70}$

⇒ $\sqrt3=\frac{AC}{70}$

⇒ $AC=70\sqrt3\text{ m}$

Hence, the correct answer is $70\sqrt3\text{ m}$.

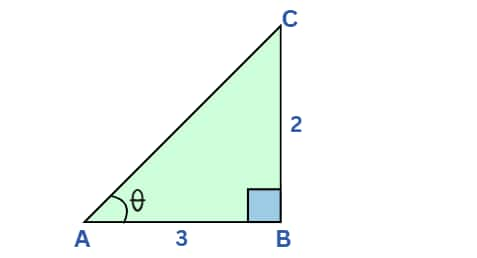
Q3. If $2 \cot \theta = 3$, find the value of $\frac{\sqrt{13} \sin \theta – 3 \tan \theta}{3 \tan \theta + \sqrt{13} \cos \theta}$

1. $\frac{1}{\sqrt{13}}$
2. $\frac{2}{\sqrt{13}}$
3. 0
4. $\frac{2}{3}$

Hint: $\cot \theta=\frac{\text{Base}}{\text{Perpendicular}} =\frac{3}{2}$, then use Pythagoras's theorem to find the hypotenuse.

Answer:

$2 \cot \theta = 3$

$⇒\cot \theta=\frac{3}{2}$

$⇒\frac{\text{Base}}{\text{Perpendicular}} =\frac{3}{2}$

$⇒\frac{AB}{BC}= \frac{3}{2}$

Let $AB = 3k, BC = 2k$

From Pythagoras' Theorem,

$AC^{2} = AB^{2} + BC^{2}$

$⇒AC^{2} = (3k)^{2} + (2k)^{2}$

$⇒AC^{2} = 13k^2$

$⇒AC = \sqrt{13}k$

$\sin\theta = \frac{\text{Perpendicular}}{\text{Hypotenuse}} = \frac{2k}{\sqrt{13}k}=\frac{2}{\sqrt{13}}$

$\cos\theta = \frac{\text{Base}}{\text{Hypotenuse}} = \frac{3k}{\sqrt{13}k}= \frac{3}{\sqrt{13}}$

$\tan \theta = \frac{\text{Perpendicular}}{\text{Base}} = \frac{2k}{3k}=\frac{2}{3}$

Putting these values in the equation, we get,

$=\frac{\sqrt{13} \sin \theta – 3 \tan \theta}{3 \tan \theta + \sqrt{13} \cos \theta}$

$=\frac{\sqrt{13} \times \frac{2}{\sqrt{13}} - 3 \times \frac{2}{3}}{3 \times\frac{2}{3} + \sqrt{13} \times \frac{3}{\sqrt{13}}}$

$=0$

Hence, the correct answer is 0.

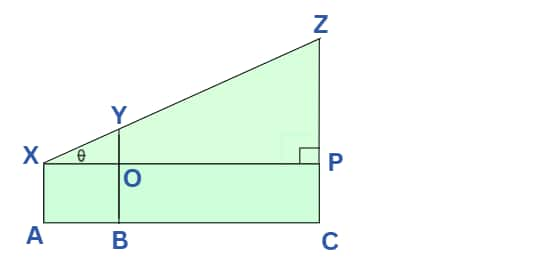
Q4. Subhas, a 3.15 m tall tree, and an 11.25 m tall building are positioned such that their feet on the ground are collinear and the tree is located between Subhas and the building. The tree is located at a distance of 7.5 m from Subhas and a distance of 45 m from the building. Further, the eyes of Subhas, the top of the tree, and the top of the building fall in one line. Find the height (in m ) from the ground at which Subhas's eyes are situated.

1. 1.75
2. 1.6
3. 1.8
4. 1.5

Hint: Assume the required height as $h$. Draw a figure according to the given data. Solve for $h$ using the trigonometric ratios.

Answer:

Let XA be Subhas, YB be the tree, and ZC be the building.

YB = 3.15 m

ZC = 11.25 m

AB = 7.5 m

BC = 45 m

XO = AB = 7.5 m

OP = BC = 45 m

⇒ XP = XO + OP = 7.5 + 45 = 52.5 m

Let the height from the ground at which Subhas's eyes are situated be $h$.

OY = BY – OB = 3.15 – $h$

PZ = ZC – PC = 11.25 – $h$

Let the angle of elevation be $\theta$.

In $\triangle$XPZ, $\tan \theta = \frac{\text{PZ}}{\text{PX}} = \frac{11.25-h}{52.5}$ -----------(i)

In $\triangle$XOY, $\tan \theta = \frac{\text{OY}}{\text{OX}} = \frac{3.15-h}{7.5}$ ------------(ii)

$⇒ \frac{11.25-h}{52.5} = \frac{3.15-h}{7.5}$

$⇒ \frac{11.25-h}{7} = \frac{3.15-h}{1}$

$⇒11.25-h = 7(3.15-h)$

$⇒11.25-h = 22.05-7h$

$⇒6h = 10.8$

$\therefore h = \frac{10.8}{6} = 1.8$ m

Hence, the correct answer is 1.8.

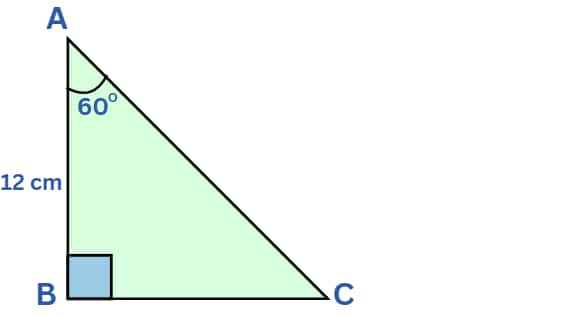
Q5. If $\triangle A B C$ is right angled at $B, A B=12 \mathrm{~cm}$ and $\angle C A B=60^{\circ}$, determine the length of $BC$.

1. $24 \sqrt{3} \mathrm{~cm}$
2. $12 \mathrm{~cm}$
3. $12 \sqrt{2} \mathrm{~cm}$
4. $12 \sqrt{3} \mathrm{~cm}$

Hint: Use the trigonometric ratio involving AB and BC.

Answer:

Given, $\triangle$ABC is right angled at B, where AB = 12 cm and $\angle$CAB = 60°

By using the trigonometric ratio involving AB and BC.

To $\angle$CAB, AB is the adjacent side and BC is the opposite side.

$\tan\angle CAB$ = $\tan 60°$ = $\frac{BC}{AB}$

⇒ $\sqrt3=\frac{BC}{12}$

$\therefore BC =12\sqrt3\ \text{cm}$

Hence, the correct answer is $12\sqrt3\ \text{cm}$.

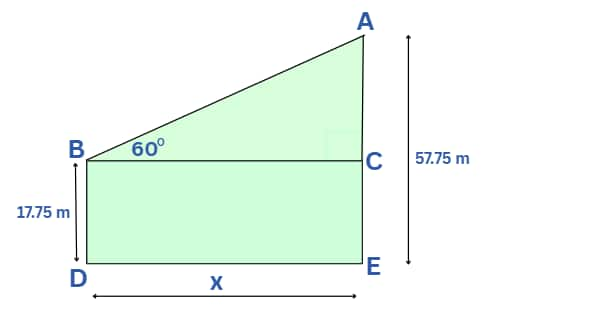
Q6. From the top of an upright pole 17.75 m high, the angle of elevation of the top of an upright tower was 60°. If the tower was 57.75 m tall, how far away (in m) from the foot of the pole was the foot of the tower?

1. $40 \sqrt{3}$
2. $\frac{151 \sqrt{3}}{6}$
3. $\frac{77}{4} \sqrt{3}$
4. $\frac{40 \sqrt{3}}{3}$

Hint: Use $\tan\theta=\frac{\text{Perpendicular}}{\text{Base}}$

Answer:

We have to find the value of $x$.

In $\triangle ABC,$

$\tan60° = \frac{AC}{BC}$

We know, $CE=BD$

⇒ $AC=AE-CE$

⇒ $AC=57.75-17.75$

⇒ $AC=40$

In $\triangle ABC,$

$\tan60° = \frac{40}{x}$

⇒ $\sqrt3=\frac{40}{x}$

⇒ $x=\frac{40}{\sqrt3}$

⇒ $x=\frac{40\sqrt3}{3}$ m

Hence, the correct answer is $\frac{40\sqrt3}{3}$.

Q7. The value of $(\sin^445°+ \cos^460°) + (\tan^445°+ \cot^445°)$ is:

1. $\frac{37}{16}$
2. $\frac{33}{16}$
3. $\frac{35}{16}$
4. $\frac{39}{16}$

Hint: $\sin45°=\frac{1}{\sqrt2},\cos60°=\frac{1}{2},\tan45°=1$ and $\cot45°=1$

Answer:

Given: $(\sin^445°+ \cos^460°) + (\tan^445°+ \cot^445°)$

= $(\frac{1}{\sqrt2})^4 + (\frac{1}{2})^4 + (1)^4 + (1)^4$

= $\frac{1}{4} + \frac{1}{16} + 1 + 1$

= $\frac{4+1+16+16}{16}$

= $\frac{37}{16}$

Hence, the correct answer is $\frac{37}{16}$.

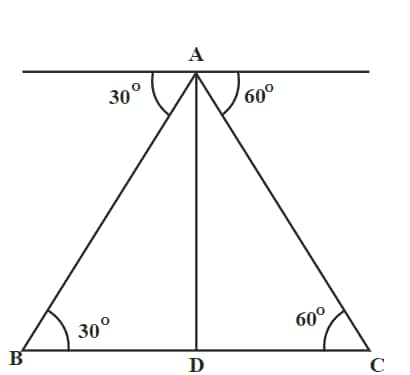
Q8. Two ships are on the opposite of a lighthouse such that all three of them are collinear. The angles of depression of the two ships from the top of the lighthouse are 30° and 60°. If the ships are $230 \sqrt{3}$ m apart, then find the height of the lighthouse (in m).

1. 175.4
2. 165.2
3. 172.5
4. 180.5

Hint: Use the formula: $\tan\theta=\frac{\text{Perpendicular}}{\text{Base}}$

Answer:

Given: The distance between the ships is BC = $230\sqrt3$ m

Let the height of the lighthouse AD be $h$ m.

From $\triangle$ABD we get,

$\tan30°=\frac{AD}{BD}$ ⇒ BD = $h\sqrt3$

Again from $\triangle$ACD we get,

$\tan60°=\frac{AD}{CD}$ ⇒ CD = $\frac{h}{\sqrt3}$

According to the question,

$h\sqrt3+\frac{h}{\sqrt3}=230\sqrt3$

⇒ $3h+h=690$

⇒ $4h=690$

⇒ $h=\frac{690}{4}=172.5$ m

Hence, the correct answer is 172.5 m.

Q9. If $\tan (A+B)=\sqrt{3}$ and $\tan (A-B)=\frac{1}{\sqrt{3}}; 0°<(A+B)<90°; A > B$, then the values of $A$ and $B$ are respectively:

1. 45° and 15°
2. 15° and 45°
3. 30° and 30°
4. 60° and 30°

Hint: $\sqrt{3}=\tan60°$ and $\frac{1}{\sqrt{3}}=\tan30°$

Answer:

Given: $\tan (A+B)=\sqrt{3}$ and $\tan (A-B)=\frac{1}{\sqrt{3}}$

$\tan (A+B)=\sqrt{3}=\tan60°$

⇒ $A+B=60°$ .........................(1)

Also, $\tan (A-B)=\frac{1}{\sqrt{3}}=\tan30°$

⇒ $A-B=30°$ ............................(2)

Solving equations (1) and (2) we get,

$A=45°$ and $B=15°$

Hence, the correct answer is 45° and 15°.

Q10. A person 1.8 metres tall is $30 \sqrt{3}$ metres away from a tower. If the angle of elevation from his eye to the top of the tower is 30°, then what is the height (in m) of the tower?

1. 32.5
2. 37.8
3. 30.5
4. 31.8

Hint: Find the height of the tower using the formulas, $\tan 30^{\circ}=\frac{1}{\sqrt3}$ and $\tan \theta=\frac{\text{Perpendicular}}{\text{Base}}$.

Answer:

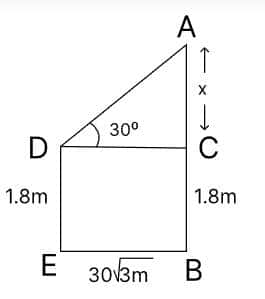
Given: A person 1.8 metres tall is $30 \sqrt{3}$ metres away from a tower.

The angle of elevation from his eye to the top of the tower is $30^{\circ}$.

We know the formulas, $\tan 30^{\circ}=\frac{1}{\sqrt3}$ and $\tan \theta=\frac{\text{Perpendicular}}{\text{Base}}$.

Let the tower's height and the person's height be AB and DE, respectively.

In $\triangle ACD$,

$\frac{AC}{DC}=\tan 30^{\circ}$

⇒ $\frac{x}{30\sqrt3}=\frac{1}{\sqrt3}$

⇒ $x=30$ m

The height of the tower AB = 30 + 1.8 = 31.8 m

Hence, the correct answer is 31.8 m.

List of Topics Related to the Trigonometric Ratios

This section covers all the essential and advanced subtopics linked to Trigonometric Ratios, including their formulas, identities, standard angles, and applications in various classes and competitive exams.

NCERT Resources

This section provides essential NCERT resources for Class 11 Chapter 3 – Trigonometric Functions, designed to strengthen your conceptual understanding. You'll find detailed notes, step-by-step NCERT solutions, and NCERT Exemplar problems, making it easier to master Trigonometric Ratios.

NCERT Class 11 Chapter 3 Trigonometric Functions Notes

NCERT Class 11 Chapter 3 Trigonometric Functions Solutions

NCERT Exemplar Class 11 Chapter 3 Trigonometric Functions

Practice Questions

Sharpen your skills with a variety of trigonometric ratio practice questions, from basic identification to complex applications. These questions are crucial for school exams and competitive tests, with step-by-step solutions.

Trigonometric Ratios - Practice Now

Below is the list of the next topics which you can practice: