Law of Sine - Definition, Proof, Formula, Applications and Example

Overview of a Triangle

A triangle is a polygon with 3 sides. A triangle is more special as compared to other polygons as it is the polygon having the least number of sides. A triangle has six main elements: three sides and three angles. There are different rules and theorems for triangles that relate their sides and angles, such as the Pythagoras theorem, the sine rule, and the law of cosines, which helps in finding unknown sides or angles.

A few standard symbols to represent elements of the triangle:

In ΔABC, the angles are denoted by capital letters A, B, and C, and the length of the sides opposite to these angles are denoted by small letters a, b, and c, respectively.

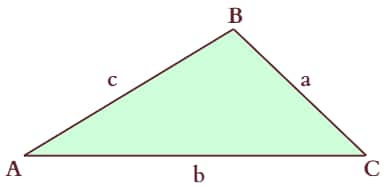
The following symbols in relation to $\triangle A B C$ are universally adopted.
Angles: $\angle B A C=\angle A, \angle A B C= \angle B, \angle B C A= \angle C$
Sides: $A B=c, A C=b$, and $B C=a$
Semi-perimeter of the $\triangle \mathrm{ABC}$, is $s=\frac{a+b+c}{2}$ and it is denoted by s . So, the perimeter of $\triangle A B C$ is $2 s=a+b+c$.

The area of a triangle is denoted by $S$ or $\Delta$.
For any $\triangle A B C$,
- $\angle A + \angle B + \angle C=180^{\circ}$
- $a+b>c, b+c>a$ and $c+a>b$
- $a>0, b>0, c>0$

These properties form the foundation for various triangle theorems, including the sine rule and the law of cosines, which establish a relationship between the sides and angles of a triangle.

Law of Sines: Definition

The law of sines connects the angle of a triangle with the length of its sides. It is used to find the unknown length or angle of a triangle.

Law of Sine Statement

The law of sines states that in any triangle, the ratio of the sine of one of the angles to the length of its opposite side will be equal to the other two ratios of the sine of the angle measured to the opposite side.

In other words,

The law of sine states that "In a triangle, side “$a$” divided by the sine of angle A is equal to side “$b$” divided by the sine of angle B is equal to side “$c$” divided by the sine of angle C."

$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}=2 \mathrm{R}$

Where R is the circumradius of a triangle.

• $a, b, c$ are the sides of the triangle

• $\angle A, \angle B, \angle C$ are the opposite angles

Key Points:

• This relation holds true for all types of triangles (acute, obtuse, and scalene).

• It is especially useful for Law of Sines examples in solving missing sides or angles.

• In advanced problems like the Law of Sines parallelogram case, this formula helps extend the concept to quadrilaterals.

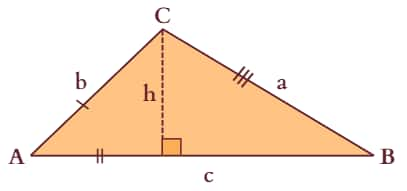Law of Sines

Law of Sines Proof

Using right triangle relationships, we know:

$ \sin A = \dfrac{h}{b} $ and $ \sin B = \dfrac{h}{a} $

Solving both equations for $h$:

$ h = b \sin A $ and $ h = a \sin B $

Equating the two expressions:

$ b \sin A = a \sin B $

Dividing both sides by $ab$:

$ \dfrac{\sin A}{a} = \dfrac{\sin B}{b} $

Similarly, using the altitude from the other vertex, we get:

$ \dfrac{\sin A}{a} = \dfrac{\sin C}{c} $ and $ \dfrac{\sin B}{b} = \dfrac{\sin C}{c} $

Therefore, collectively:

$ \dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c} $

Sine Formula Geometric Proof

Take the same triangle $ABC$ and draw its circumcircle (circle passing through all vertices).

The diameter of the circumcircle is $2R$, where $R$ is the circumradius.

By circle property:
$ \sin A = \dfrac{a}{2R}, \quad \sin B = \dfrac{b}{2R}, \quad \sin C = \dfrac{c}{2R} $

Rearranging gives:
$ \dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R $

This proof highlights the direct connection of the Law of Sines with circle geometry, often used in advanced Law of Sines examples.

Applications of Sine Law

The Law of Sines plays a vital role in solving different kinds of triangle-related problems, both in mathematics and in practical scenarios. It is widely used to find missing angles, sides. Below are the major areas where it is applied.

Solving Triangles Using the Law of Sines

• One of the most common uses of the Law of Sines is solving oblique triangles (ASA, AAS, or SSA cases).

• If two angles and one side are known, you can easily find the remaining side using:
  $ \dfrac{a}{\sin A} = \dfrac{b}{\sin B} $

• This method is frequently taught in Law of Sines Class 11 and Class 12 to handle non-right triangle problems.

• Many Law of Sines examples in exams involve finding unknown angles when two sides and an angle are given.

Law of Sines Parallelogram Case

• Apart from triangles, the rule can also extend to certain quadrilaterals like a parallelogram.

• By dividing a parallelogram into two triangles along a diagonal, the Law of Sines formula can be applied separately in each triangle.

• Example: If $ABCD$ is a parallelogram with diagonal $AC$, then using
  $ \dfrac{AB}{\sin \angle ADC} = \dfrac{AC}{\sin \angle DAC} $ helps in solving unknown sides or angles.

Law of Sines vs Law of Cosines

Understanding the differences between the Law of Sines and the Law of Cosines is important for solving various types of triangle problems. Each rule serves its own purpose depending on the information given. Below are the key comparisons and applications.

Difference Between Law of Sines and Law of Cosines

Both the Law of Sines and the Law of Cosines are essential tools in trigonometry, but they apply to different situations.

When to Use Law of Sines and When to Use Law of Cosines

• Use the Law of Sines when:

  • You know two angles and one side (ASA or AAS).

  • You know two sides and a non-included angle (SSA).

  • Quick ratio-based calculation is required.

• Use the Law of Cosines when:

  • You know two sides and the included angle (SAS).

  • You know all three sides (SSS).

  • Angle calculation requires direct application without ratios.

Combined Use in Complex Triangle Problems

• In advanced problems, especially in Class 12 trigonometry and competitive exams, both laws are often used together.

• Example: Use Law of Cosines first to find an unknown angle, then apply the Law of Sines to solve for other sides.

• This combined approach is often tested in JEE Main, JEE Advanced questions where multi-step triangle solving is required.

Problems Based on the Sine rule

Example 1: In Triangle PQR, if $(p+q+r)(p+q-r)=2 p q$ then what is value of angle $R$?

Solution: Sides of the $\triangle ABC$

$AB = c, \; AC = b, \; BC = a$

$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$

$(p+q+r)(p+q-r) = 2pq$

$(p+q)^2 - r^2 = 2pq$

$p^2 + q^2 - r^2 = 0$

$\angle R = \frac{\pi}{2}$

Example 2: For what and only what values of $\alpha$ lying between 0 and $\pi$ is the inequality $\sin \alpha \cos ^3 \alpha>\sin ^3 \alpha \cos \alpha$ valid?

Solution:

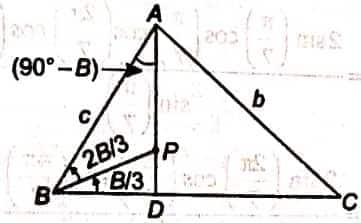
In $\Delta ABP$, by sine rule

$\frac{AP}{\sin \left(\tfrac{2B}{3}\right)} = \frac{c}{\sin \left(90^{\circ} + \tfrac{B}{3}\right)}$

$\therefore \; AP = \frac{c \sin \left(\tfrac{2B}{3}\right)}{\cos \left(\tfrac{B}{3}\right)}$

$= \frac{2c \sin \left(\tfrac{B}{3}\right) \cos \left(\tfrac{B}{3}\right)}{\cos \left(\tfrac{B}{3}\right)}$

$= 2c \sin \left(\tfrac{B}{3}\right)$

Example 3: If ABC is a triangle and $\mathrm{AB}=2, B C=\sqrt{3}$ then what is the maximum possible value of $A$ ?

Solution: In ΔABC, the angles are denoted by capital letters A, B, and C, and the length of the sides opposite to these angles are denoted by small letters a, b, and c respectively.

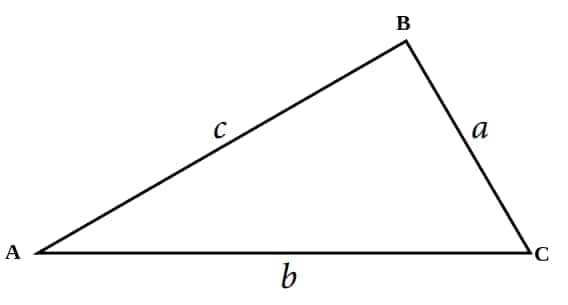
$\angle BAC = \angle A$

$\angle ABC = \angle B$

$\angle BCA = \angle C$

$\text{Sides of the } \triangle ABC: \; AB = c, \; AC = b, \; BC = a$

$\text{Collectively, these relationships are called the Law of Sines}$

$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$

$\frac{AB}{\sin C} = \frac{BC}{\sin A}$

$\frac{2}{\sin C} = \frac{\sqrt{3}}{\sin A}$

$\sin A = \frac{\sqrt{3}}{2} \sin C$

$\text{Maximum possible value of } A = \frac{\pi}{3}$

$\text{Hence, the answer is } \frac{\pi}{3}$

Example 4: If ABC is the triangle and $A-B=90^{\circ}$ and $\mathrm{B}=3 \mathrm{~A}$ then Find the value of B .

Solution: In ΔABC, the angles are denoted by capital letters A, B, and C, and the length of the sides opposite to these angles are denoted by small letters a, b and c respectively.

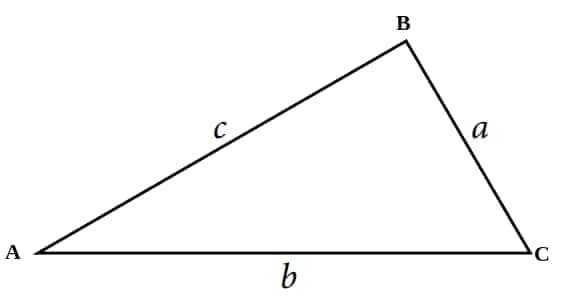
$\angle BAC = \angle A$

$\angle ABC = \angle B$

$\angle BCA = \angle C$

$\text{Sides of the } \triangle ABC: \; AB = c, \; AC = b, \; BC = a$

$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$

$\frac{a}{\sin A} = \frac{b}{\sin B}$

$\frac{b}{3 \sin (90+B)} = \frac{b}{\sin B}$

Hence, the answer is 3.

Example 5: In triangle PQR, $p^2, q^2$ and $r^2$ are in $A . P$. Then $\cot P, \cot Q, \cot R$ are in

Solution:

$p^2, q^2, r^2 \text{ are in A.P.}$

$r^2 - q^2 = q^2 - p^2$

$\sin^2 R - \sin^2 Q = \sin^2 Q - \sin^2 P$

$\sin (R+Q)\sin (R-Q) = \sin (Q+P)\sin (Q-P)$

$\sin (\pi - P)(\sin R \cos Q - \cos R \sin Q) = \sin (\pi - R)(\sin Q \cos P - \cos Q \sin P)$

$\sin P (\sin R \cos Q - \cos R \sin Q) = \sin R (\sin Q \cos P - \cos Q \sin P)$

$\text{Divide both sides by } \sin P \sin Q \sin R$

$\cot Q - \cot R = \cot P - \cot Q$

$\cot P, \cot Q, \cot R \text{ are in A.P.}$

Hence, the answer is cot P, cot Q, and cot R are in AP.

List of Topics related to Law of Sines

The Law of Sines connects with several other important trigonometric concepts that help in solving advanced problems and equations. These topics has its applications and build a deeper understanding of trigonometric relationships. Below are the related topics you can explore.

NCERT Resources

NCERT study materials provide a strong foundation for understanding concepts in trigonometry, especially for competitive exams and school-level preparation. They offer clear explanations, step-by-step solutions, and additional practice problems. Below are the key NCERT resources for Chapter 3: Trigonometric Functions.

NCERT Class 11 Maths Notes for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Solutions for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Exemplar Solutions for Chapter 3 - Trigonometric Functions

Practice Questions based on Law of Sines

Practice is the key to mastering trigonometric concepts like the Law of Sines and related formulas. Solving a variety of problems helps strengthen understanding and improve problem-solving speed. Below are the practice question sets you can try.

Law Of Sines - Practice Question MCQ

Students can practice the related questions from the links shared below: