Linear Combination of Vectors
Before studying about linear combination of vectors, let's revise about vectors. A quantity that has magnitude as well as a direction in space and follows the triangle law of addition is called a vector quantity, e.g., velocity, force, displacement, etc. A vector is represented by a directed line segment (an arrow). In real life, we use vectors for tracking objects that are in motion, and localization of places and things.
This Story also Contains
- Linear Combination of Vectors
- Test of collinearity of three points
- Important point
- Solved Examples Based on Linear Combination of Vectors
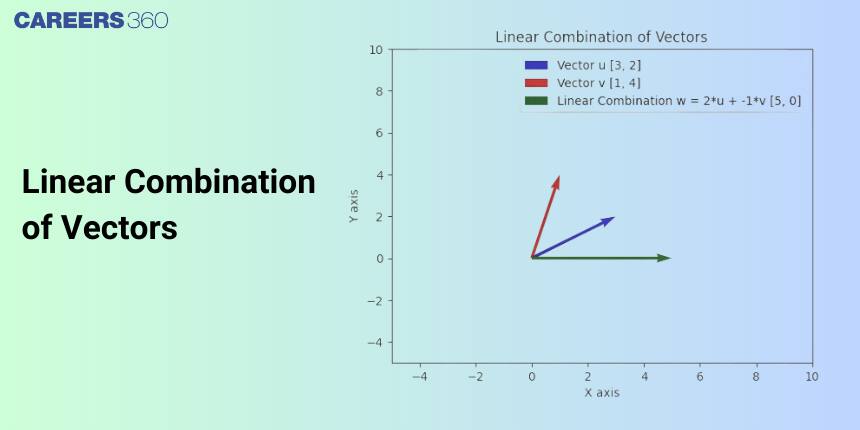
In this article, we will cover the concept of Linear Combination of Vectors. This topic falls under the broader category of Vector Algebra, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of five questions have been asked on this topic in JEE Main from 2013 to 2023 including one in 2022.
Linear Combination of Vectors
A vector $\vec{r}$ is said to be a linear combination of vectors $\vec{a}_1, \vec{a}_2, \vec{a}_3 \ldots \ldots, \vec{a}_n$ if there exist scalars $\lambda_1, \lambda_2, \lambda_3, \ldots \ldots, \lambda_n$ such that
$
\vec{r}=\lambda_1 \vec{a}_1+\lambda_2 \vec{a}_2+\lambda_3 \vec{a}_3+\ldots \ldots+\lambda_n \vec{a}_n
$
For example:
vectors $\vec{r}_1=\vec{a}+2 \vec{b}+3 \vec{c}$ and $\vec{r}_2=\vec{a}-4 \vec{b}-9 \vec{c}$ are linear combination of the vectors $\vec{a}, \vec{b}$ and $\vec{c}$.
Linear Independent Vectors
A system of vectors $\vec{a}_1, \vec{a}_2, \vec{a}_3 \ldots \ldots, \vec{a}_n$ is said to be linearly independent, if
$
\begin{array}{ll}
& \lambda_1 \vec{a}_1+\lambda_2 \vec{a}_2+\lambda_3 \vec{a}_3+\ldots \ldots+\lambda_n \vec{a}_n=0 \\
\Rightarrow \quad & \lambda_1=\lambda_2=\lambda_3=\ldots \ldots=\lambda_n=0
\end{array}
$
It can be easily verified that
1. A pair of non-collinear vectors ( say a1 and a2 ) are linearly independent.
Let $\vec{a}_1$ and $\vec{a}_2$ are two non-collinear vectors such that $\lambda_1 \vec{a}_1+\lambda_2 \vec{a}_2=0$.
Let, $\quad \lambda_1, \lambda_2 \neq 0$
$\Rightarrow \quad \vec{a}_1=-\frac{\lambda_2}{\lambda_1} \vec{a}_2$
Now, $-\frac{\lambda_2}{\lambda_1}$ is a scalar, because $\lambda_1$ and $\lambda_2$ are scalars.
Hence, eq (i) expresses $\vec{a}_1$ as product of $\vec{a}_2$ by a scalar, so that $\vec{a}_1$ and $\vec{a}_2$ are collinear.
Which contradict the given fact because $\overrightarrow{a_1}$ and $\overrightarrow{a_2}$ are given to be non - collinear.
Th thus, our supposition that $\lambda_1 \neq 0$ and $\lambda_2 \neq 0$ is wrong.
Hence, $\lambda_1=0$ and $\lambda_2=0$
2. A triad of non-coplanar vector is linearly independent
If a, b, c are three non-zero, non-coplanar vectors and x, y, z are three scalars such that
$\begin{array}{r}x a+y b+z c=0 \\ \text { Then, } x=y=z=0\end{array}$
Proof: It is given that $\mathrm{xa}+\mathrm{yb}+\mathrm{zc}=0$
Suppose that $x \neq 0$
Then Eq. (i) can be written as
$
\begin{gathered}
x=-y b-z \mathrm{c} \\
\Rightarrow \mathrm{a}=-\frac{y}{x} \mathrm{~b}-\frac{z}{x} \mathrm{c} \quad \ldots \text { (ii) }
\end{gathered}
$
Now, $\frac{y}{x}$ and $\frac{z}{x}$ are scalars because $x, y$ are scalars. Thus, Eq. (ii) expresses an as a linear combination of $b$ and $c$. Hence, a is coplanar with b and c which is contrary to our hypothesis because a, b, and c are given to be non-coplanar. Thus, our supposition that $x \neq 0$ is wrong.
Hence, $x=0$.
Similarly, we can prove that $\mathrm{y}=0$ and $\mathrm{z}=0$.
Note: 4 vectors are always linearly dependent
A system of vectors $\vec{a}_1, \vec{a}_2, \vec{a}_3 \ldots \ldots, \vec{a}_n$ is said to be linearly dependent, if there exists scalars $\lambda_1, \lambda_2, \lambda_3, \ldots \ldots \ldots, \lambda_{\mathrm{n}}$ not all zero such that
$
\lambda_1 \vec{a}_1+\lambda_2 \vec{a}_2+\lambda_3 \vec{a}_3+\ldots \ldots+\lambda_n \vec{a}_n=0
$
It can be easily verified that
1. A pair of collinear vectors is linearly dependent.
2. A triad of coplanar vectors is linearly dependent.
Test of collinearity of three points
Let $A(\vec{a}), B(\vec{b})$ and $C(\vec{c})$, be three points in space
If we can find $x, y, z$, not all zero such that
(i) $x \vec{a}+y \vec{b}+z \vec{c}=0$ and (ii) $x+y+z=0$
Then the points $A, B$, and $C$ are collinear
Proof:
Let us suppose that points $A, B$ and $C$ are collinear and their position vectors are :, $\vec{b}$ and $\vec{c}$ respectively. Let $C$ divide the join of $\vec{a}$ and $\vec{b}$ in the ratio $y: x$
Then,
$
\begin{aligned}
& \vec{c}=\frac{x \vec{a}+y \vec{b}}{x+y} \\
& x \vec{a}+y \vec{b}-(x+y) \vec{c}=\overrightarrow{0} \\
& x \vec{a}+y \vec{b}+z \vec{c}=\overrightarrow{0}, \text { where } z=-(x+y) \\
& x+y+z=x+y-(x+y)=0
\end{aligned}
$
Hence, the three points $A, B$, and $C$ are collinear.
Theorem 1:
If $\vec{a}$ and $\vec{b}$ are two non-zero, non-collinear vectors, then every vector $\vec{r}$ coplanar with $\vec{a}$ and $\vec{b}$ can be expressed in one and only one way as a linear combination $x \vec{a}+y \vec{b}$ where $x$ and $y$ being scalars.

Proof:
Let $O$ be any point such that $\overrightarrow{O A}=\vec{a}$ and $\overrightarrow{O B}=\vec{b}$ As $\vec{r}$ is coplanar with $\vec{a}$ and $\vec{b}$, the lines $O A, O B$ and $O R$ are coplanar. Through $R$, draw lines parallel to $O A$ and $O B$, meeting them at $P$ and $Q$, respectively. Clearly,
$
\overrightarrow{\longrightarrow P}=x \overrightarrow{O A}=x \vec{a} \quad(\because \overrightarrow{O P} \text { and } \overrightarrow{\longrightarrow A} \text { are collinear vectors })
$
Also,
$
\overrightarrow{O Q}=y \overrightarrow{O B}=y \vec{b} \quad(\because \overrightarrow{O Q} \text { and } \overrightarrow{O B} \text { are collinear vectors })
$
$
\begin{aligned}
\vec{r} & =\overrightarrow{O R}=\overrightarrow{O P}+\overrightarrow{P R}=\overrightarrow{O P}+\overrightarrow{O Q} \quad(\because \overrightarrow{O Q} \text { and } \overrightarrow{P R} \text { are equal }) \\
& =x \vec{a}+y \vec{b}
\end{aligned}
$
Thus, $\vec{r}$ can be expressed in one way as a linear combination $x \vec{a}+y \vec{b}$.
Theorem 2
If $\vec{a}, \vec{b}$ and $\vec{c}$ are non-coplanar vectors, then any vector $\vec{r}$ can be uniquely expressed as a linear combination $\vec{x} \vec{a}+y \vec{b}+z \vec{c}$ where $x, y$ and $z$ being scalars.

NOTE:
1.
If vectors $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}, \vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$ and $\vec{c}=c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}$ are coplanar, then
$
\left|\begin{array}{lll}
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
c_1 & c_2 & c_3
\end{array}\right|=0
$
(Proof of this will be seen in the concept of Scalar triple Product)
2.
If vectors $x_1 \vec{a}+y_1 \vec{b}+z_1 \vec{c}, \quad x_2 \vec{a}+y_2 \vec{b}+z_2 \vec{c}$ and $x_3 \vec{a}+y_3 \vec{b}+z_3 \vec{c}$ are coplanar where $\vec{a}, \vec{b}$ and $\vec{c}$ are non-coplanar. Then,
$
\left|\begin{array}{lll}
x_1 & y_1 & z_1 \\
x_2 & y_2 & z_2 \\
x_3 & y_3 & z_3
\end{array}\right|=0
$
Important point
1) Two collinear vectors are always linearly dependent.
2) Two non-collinear non-zero vectors are always linearly independent.
3) Three coplanar vectors are always linearly dependent.
4) Three non-coplanar non-zero vectors are always linearly independent.
5) More than three vectors are always linearly dependent.
Recommended Video Based on Linear Combination of Vectors
Solved Examples Based on Linear Combination of Vectors
Example 1: Let the vectors $\overrightarrow{\mathrm{a}}=(1+\mathrm{t}) \hat{\mathrm{i}}+(1-\mathrm{t}) \hat{\mathrm{j}}+\hat{\mathrm{k}}, \overrightarrow{\mathrm{b}}=(1-\mathrm{t}) \hat{\mathrm{i}}+(1+\mathrm{t}) \hat{\mathrm{j}}+2 \hat{\mathrm{k}}$ and $\overrightarrow{\mathrm{c}}=\mathrm{t} \hat{\mathrm{i}}-\mathrm{t} \hat{\mathrm{j}}+\hat{\mathrm{k}}, \mathrm{t} \in \mathbf{R}$ be such that for $\alpha, \beta, \gamma \in \mathbf{R}, \alpha \vec{a}+\beta \vec{b}+\gamma \vec{c}=\overrightarrow{0} \Rightarrow \alpha=\beta=\gamma=0$. Then, the set of all values of t is: [JEE MAINS 2022]
Solution
By its given condition $\vec{a}, \vec{b}, \vec{c}$ are linearly independent vectors
$
\begin{aligned}
& \Rightarrow[\vec{a} \vec{b} \vec{c}] \neq 0 \cdots(1) \\
& \text { Now }[\vec{a} \vec{b} \vec{c}] \\
& =\left|\begin{array}{ccc}
1+t & 1-t & 1 \\
1-t & 1+t & 2 \\
t & -t & 1
\end{array}\right|
\end{aligned}
$
$
\begin{aligned}
& c_2 \rightarrow c_1+c_2 \\
& \left|\begin{array}{ccc}
1+t & 2 & 1 \\
1-t & 2 & 2 \\
t & 0 & 1
\end{array}\right|=2\left|\begin{array}{ccc}
1+t & 1 & 1 \\
1-t & 1 & 2 \\
t & 0 & 1
\end{array}\right| \\
& =2[(1+t)-(1-t)+t] \\
& =2[3 \mathrm{t}]=6 \mathrm{t} \\
& {[\tilde{\mathrm{a}} \tilde{\mathrm{b}} \tilde{\mathrm{c}}] \neq 0 \Rightarrow \mathrm{t} \neq 0}
\end{aligned}
$
Hence, the answer is equal to $\mathbf{R}-\{0\}$
Example 2: If $\vec{a}=2 \vec{p}+3 \vec{q}-\vec{r}, \vec{b}=\vec{p}-2 \vec{q}+2 \vec{r}, \vec{c}=-2 \vec{p}+\vec{q}-2 \vec{r}$ and $\vec{R}=3 \vec{p}-\vec{q}+2 \vec{r}$, then $\vec{R}$ equals ( $\vec{p}, \vec{q}, \vec{r}$ are non-coplanar)
Solution: Linear combination of vectors- $\vec{r}=l \vec{a}+m \vec{b}+n \vec{c}$
Any vectors $\vec{r}$ in space can be written as a linear combination of 3 non-coplanar vectors.
$
\begin{aligned}
& \text { Let } \vec{R}=x \vec{a}+y \vec{b}+z \vec{c} \\
& \Rightarrow 3 \vec{p}-\vec{q}+2 \vec{r}=(2 x+y-2 z) \vec{p}+(3 x-2 y+z) \vec{q}+(-x+2 y-2 z) \vec{r}
\end{aligned}
$
$\because \vec{p}, \vec{q}$, and $\gamma$ are non-coplanar, so
$\alpha \vec{p}+\beta \vec{q}+\gamma \vec{r}=\overrightarrow{0}$ only when $\alpha=0, \beta=0, \gamma=0$
$
2 x+y-2 z=3 ; 3 x-2 y+z=-1 ;-x+2 y-2 z=2
$
on solving, we get
$
x=2, y=5, z=3
$
$
\therefore \vec{R}=2 \vec{a}+5 \vec{b}+3 \vec{c}
$
Hence, the answer is $2 \vec{a}+5 \vec{b}+3 \vec{c}$
Example 3: $3 \lambda c+2 \mu(a \times b)=0$ then
Solution: $3 \lambda \vec{c}+2 \mu(\vec{a} \times \vec{b})=0$
Where $\lambda$ and $\mu$ are scaler constant
$3 \lambda \vec{c}=-2 \mu(\vec{a} \times \vec{b})$
On comparing vectors
We can say that $\vec{c}=-(\vec{a} \times \vec{b})$
Hence
$3 \lambda \vec{c}=-2 \mu(\vec{c})$
Or
$3 \lambda=-2 \mu$
$3 \lambda+2 \mu=0$
Hence, the answer is $3 \lambda+2 \mu=0$
Example 4: Let $\vec{r}=\hat{i}-\hat{k}, \vec{a}=\hat{i}-\hat{j}+\hat{k}, \vec{b}=2 \hat{i}-3 \hat{j}+4 \hat{k}$, then linear combinations of $\vec{a}$ and $\vec{b}$ equal $\vec{r}$ ?
Solution
$
3 \vec{a}-\vec{b}=3(\hat{i}-\hat{j}+\hat{k})-(2 \hat{i}-3 \hat{j}+4 \hat{k})=\hat{i}-\hat{k}=\vec{r}
$
Hence, the answer is $\vec{r}=3 \vec{a}-\vec{b}$