Lagrange's Identity: Definition, Formula, Proof & Example

Introduction to Lagrange’s Identity in Vector Algebra

Lagrange’s Identity in vector algebra establishes a key relationship between the dot and cross products of vectors. It offers valuable insights into vector magnitudes, orthogonality, and the geometry of three-dimensional space, making it essential for both theoretical and applied mathematics.

What is the Lagrange Identity in Vector Form?

Lagrange’s Identity in vector form is a relation between the dot and cross products of two vectors. It expresses how the magnitude of the cross product relates to the lengths and angle between the vectors. The identity is written as:

$(\vec{a} \times \vec{b}) \cdot (\vec{a} \times \vec{b}) = (\vec{a} \cdot \vec{a})(\vec{b} \cdot \vec{b}) - (\vec{a} \cdot \vec{b})^2$

Langrange's Identity is a formula that gives the length of the wedge product of two vectors, which is the area of the parallelogram, in terms of the dot products of the two vectors.

$\begin{aligned}(\vec{a} \times \vec{b}) \cdot(\vec{c} \times \vec{d}) & =\left|\begin{array}{ll}\vec{a} \cdot \vec{c} & \vec{a} \cdot \vec{d} \\ \vec{b} \cdot \vec{c} & \vec{b} \cdot \vec{d}\end{array}\right| \\ & =(\vec{a} \cdot \vec{c})(\vec{b} \cdot \vec{d})-(\vec{a} \cdot \vec{d})(\vec{b} \cdot \vec{c})\end{aligned}$

Significance of Lagrange Identity in Vector Operations

Lagrange's identity is useful in simplifying vector expressions involving both dot and cross products. It helps in avoiding trigonometric calculations when dealing with vector magnitudes and angles. The identity also proves essential in applications like computing surface areas, analysing forces in physics, and verifying vector orthogonality.

By relating $(\vec{a} \times \vec{b})^2$ to dot products, Lagrange's identity supports efficient vector calculations in 3D space.

Mathematical Form of Lagrange Identity Vector Version

Explore the precise vector form of Lagrange’s Identity, which connects the squares of dot and cross products of vectors. This mathematical expression serves as a fundamental result in vector algebra with wide-ranging applications in geometry and physics.

Lagrange’s Identity for Two Vectors in $\mathbb{R}^3$

In three-dimensional space, Lagrange’s Identity provides a relationship between the dot and cross products of two vectors. For any vectors $\vec{a}, \vec{b} \in \mathbb{R}^3$, the identity is written as:

$(\vec{a} \times \vec{b}) \cdot (\vec{a} \times \vec{b}) = (\vec{a} \cdot \vec{a})(\vec{b} \cdot \vec{b}) - (\vec{a} \cdot \vec{b})^2$

This is the most common vector form of Lagrange's identity, showing how the magnitude of the cross product relates to the dot products of the same vectors.

Statement Using Dot and Cross Products

The identity can be interpreted as:

$|\vec{a} \times \vec{b}|^2 = |\vec{a}|^2 |\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2$

Here, $|\vec{a}|^2 = \vec{a} \cdot \vec{a}$ and similarly for $\vec{b}$. This form of the Lagrange's identity vector is useful for expressing area and angles in purely algebraic terms, without needing trigonometric functions.

Algebraic Interpretation of the Identity

Algebraically, Lagrange's identity confirms that the square of the cross product’s magnitude equals the determinant of a $2 \times 2$ matrix formed by dot products:

$(\vec{a} \times \vec{b}) \cdot (\vec{a} \times \vec{b}) = \begin{vmatrix} \vec{a} \cdot \vec{a} & \vec{a} \cdot \vec{b} \\ \vec{b} \cdot \vec{a} & \vec{b} \cdot \vec{b} \end{vmatrix} = (\vec{a} \cdot \vec{a})(\vec{b} \cdot \vec{b}) - (\vec{a} \cdot \vec{b})^2$

This form is compact and shows how the identity combines both the magnitude and direction of vectors in a single expression.

Derivation of Lagrange’s Identity for Vectors

Understand how Lagrange’s Identity is derived using vector operations like the dot and cross product. This section walks through the proof in three dimensions, explores its link with vector triple products, and outlines how the identity extends to higher-dimensional vector spaces.

Step-by-Step Proof in Three Dimensions

To derive Lagrange’s Identity in $\mathbb{R}^3$, consider two vectors $\vec{a} = \langle a_1, a_2, a_3 \rangle$ and $\vec{b} = \langle b_1, b_2, b_3 \rangle$. The cross product is:

$\vec{a} \times \vec{b} = \langle a_2b_3 - a_3b_2,\ a_3b_1 - a_1b_3,\ a_1b_2 - a_2b_1 \rangle$

Taking the dot product of this with itself:

$|\vec{a} \times \vec{b}|^2 = (a_2b_3 - a_3b_2)^2 + (a_3b_1 - a_1b_3)^2 + (a_1b_2 - a_2b_1)^2$

Expanding and simplifying gives:

$|\vec{a} \times \vec{b}|^2 = (a_1^2 + a_2^2 + a_3^2)(b_1^2 + b_2^2 + b_3^2) - (a_1b_1 + a_2b_2 + a_3b_3)^2$

Which is:

$|\vec{a} \times \vec{b}|^2 = |\vec{a}|^2 |\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2$

This completes the proof of the Lagrange's identity vector form in three dimensions.

Derivation of Lagrange's Identity

$\text{Let} \quad (\overrightarrow{a} \times \overrightarrow{b}) \cdot (\overrightarrow{c} \times \overrightarrow{d}) = \overrightarrow{u} \cdot (\overrightarrow{c} \times \overrightarrow{d})$

$\text{where} \quad \overrightarrow{u} = \overrightarrow{a} \times \overrightarrow{b}$

$(\overrightarrow{u} \times \overrightarrow{c}) \cdot \overrightarrow{d} = ((\overrightarrow{a} \times \overrightarrow{b}) \times \overrightarrow{c}) \cdot \overrightarrow{d}$

$= \big( (\overrightarrow{c} \cdot \overrightarrow{a}) \overrightarrow{b} - (\overrightarrow{c} \cdot \overrightarrow{b}) \overrightarrow{a} \big) \cdot \overrightarrow{d}$

$= (\overrightarrow{c} \cdot \overrightarrow{a})(\overrightarrow{b} \cdot \overrightarrow{d}) - (\overrightarrow{c} \cdot \overrightarrow{b})(\overrightarrow{a} \cdot \overrightarrow{d})$

$= (\overrightarrow{a} \cdot \overrightarrow{c})(\overrightarrow{b} \cdot \overrightarrow{d}) - (\overrightarrow{a} \cdot \overrightarrow{d})(\overrightarrow{b} \cdot \overrightarrow{c})$

NOTE:

$ (\vec{a} \times \vec{b}) \times (\vec{c} \times \vec{d}) = \big[ (\vec{a} \times \vec{b}) \cdot \vec{d} \big] \vec{c} - \big[ (\vec{a} \times \vec{b}) \cdot \vec{c} \big] \vec{d} $

$ = \left[ \vec{a} \quad \vec{b} \quad \vec{d} \right] \vec{c} - \left[ \vec{a} \quad \vec{b} \quad \vec{c} \right] \vec{d} $

$\Rightarrow$ Thus, vector $\overrightarrow{(a} \times \vec{b}) \times(\vec{c} \times \vec{d})$ lies in the plane of $\vec{c}$ and $\vec{d}$

If we take the dot product of two systems of vectors and get unity, then the system is called the reciprocal system of vectors.

Thus if $\tilde{\mathrm{a}}, \tilde{\mathrm{b}}$ and $\tilde{\mathrm{c}}$ are three non - coplanar vectors, and if $\overrightarrow{a^{\prime}}=\frac{\vec{b} \times \vec{c}}{\left[\begin{array}{ll}\vec{a} & \vec{b}\end{array}\right]}$, $\overrightarrow{b^{\prime}}=\frac{\vec{c} \times \vec{a}}{\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]}$ and $\overrightarrow{c^{\prime}}=\frac{\vec{a} \times \vec{b}}{\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]}$ then $\overrightarrow{a^{\prime}}, \overrightarrow{b^{\prime}}, \overrightarrow{c^{\prime}}$ are said to be the reciprocal systems vectors for vectors $\vec{a}, \vec{b}$ and $\vec{c}$.

Connection to Vector Triple Products

The identity is closely related to vector triple products. Specifically, for any vectors $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ in $\mathbb{R}^3$:

$(\vec{a} \times \vec{b}) \cdot (\vec{c} \times \vec{d}) = (\vec{a} \cdot \vec{c})(\vec{b} \cdot \vec{d}) - (\vec{a} \cdot \vec{d})(\vec{b} \cdot \vec{c})$

This extended form of Lagrange's identity appears in determinant and scalar triple product computations, helping reduce complex expressions to simple dot products.

Extensions to Higher-Dimensional Spaces

While the standard Lagrange's identity applies to vectors in $\mathbb{R}^3$, its algebraic structure can be generalised. In $\mathbb{R}^n$, a related form is:

$\sum_{1 \leq i < j \leq n} (a_ib_j - a_jb_i)^2 = \left( \sum_{i=1}^{n} a_i^2 \right)\left( \sum_{j=1}^{n} b_j^2 \right) - \left( \sum_{k=1}^{n} a_k b_k \right)^2$

This version also represents the square of the area of the parallelogram spanned by two $n$-dimensional vectors. Though the cross product is not defined in higher dimensions, this form of Lagrange's identity still holds as a pure algebraic identity.

Properties of Lagrange's Identity

Explore key properties that highlight the geometric and algebraic relationships between vectors in a reciprocal system. Understand conditions of orthogonality, self-reciprocal sets like unit vectors, and implications for non-coplanarity and scalar triple products. These properties form the foundation for deeper vector analysis in physics and mathematics.

Reciprocal System Identity:

If $\vec{a}, \vec{b}, \vec{c}$ and $\vec{a}^{,\prime}, \vec{b}^{,\prime}, \vec{c}^{,\prime}$ form a reciprocal system of vectors, then:

$\vec{a} \cdot \vec{a}^{\,\prime} = \frac{\vec{a} \cdot (\vec{b} \times \vec{c})}{[\vec{a}\ \vec{b}\ \vec{c}]} = \frac{[\vec{a}\ \vec{b}\ \vec{c}]}{[\vec{a}\ \vec{b}\ \vec{c}]} = 1$

Similarly:

$\vec{b} \cdot \vec{b}^{\,\prime} = \vec{c} \cdot \vec{c}^{\,\prime} = 1$

Due to this property, the two systems are called reciprocal systems of vectors.

Orthogonality Across Systems:

All other cross-dot products between vectors of opposite systems vanish:

$\vec{a} \cdot \vec{b}^{\,\prime} = \vec{a} \cdot \vec{c}^{\,\prime} = \vec{b} \cdot \vec{a}^{\,\prime} = \vec{b} \cdot \vec{c}^{\,\prime} = \vec{c} \cdot \vec{a}^{\,\prime} = \vec{c} \cdot \vec{b}^{\,\prime} = 0$

Scalar Triple Product of Reciprocal Systems:

$[\vec{a}\ \vec{b}\ \vec{c}] \cdot [\vec{a}^{\,\prime}\ \vec{b}^{\,\prime}\ \vec{c}^{\,\prime}] = 1$

Here, both expressions represent scalar triple products (or determinants), and this equality confirms the reciprocal nature.

Orthogonal Triad is Self-Reciprocal:

The standard orthogonal unit vectors $\hat{i}, \hat{j}, \hat{k}$ form a self-reciprocal system, meaning:

$\hat{i}^{\,\prime} = \hat{i}, \quad \hat{j}^{\,\prime} = \hat{j}, \quad \hat{k}^{\,\prime} = \hat{k}$

Non-Coplanarity and Reciprocal Systems:

If $\vec{a}, \vec{b}, \vec{c}$ are non-coplanar, then their reciprocal system $\vec{a}^{,\prime}, \vec{b}^{,\prime}, \vec{c}^{,\prime}$ is also non-coplanar.

This is because:

$[\vec{a}^{\,\prime}\ \vec{b}^{\,\prime}\ \vec{c}^{\,\prime}] \cdot [\vec{a}\ \vec{b}\ \vec{c}] = 1$

And since:

$[\vec{a}\ \vec{b}\ \vec{c}] \neq 0 \quad \Rightarrow \quad \frac{1}{[\vec{a}\ \vec{b}\ \vec{c}]} \neq 0$

This implies the determinant of the reciprocal system is also non-zero, hence non-coplanar.

Solved Examples Based on Lagrange's Identity

Example 1: Let $\mathrm{a}, \mathrm{b}$ be two vectors such that $|\mathrm{a} . \mathrm{b}|^2=9$ and $|\mathrm{a} \times \mathrm{b}|^2=75$. Then $|\vec{a}|^2$ is equal to $\qquad$
Solution:

$|\tilde{a} + \tilde{b}|^2 = |\tilde{a}|^2 + 2|\tilde{b}|^2$

$\Rightarrow |\tilde{a}|^2 + |\tilde{b}|^2 + 2 \tilde{a} \cdot \tilde{b} = |\tilde{a}|^2 + 2|\tilde{b}|^2$

$\Rightarrow |\tilde{b}|^2 + 2 \tilde{a} \cdot \tilde{b} = 2 |\tilde{b}|^2 = 6$

$\Rightarrow |\tilde{b}| = \sqrt{6}$

$|\tilde{a} \cdot \tilde{b}|^2 + |\tilde{a} \times \tilde{b}|^2 = |\tilde{a}|^2 |\tilde{b}|^2$

$\Rightarrow 9 + 75 = |\tilde{a}|^2 \cdot 6$

$\Rightarrow |\tilde{a}|^2 = \frac{84}{6} = 14$

Hence, the answer is 14

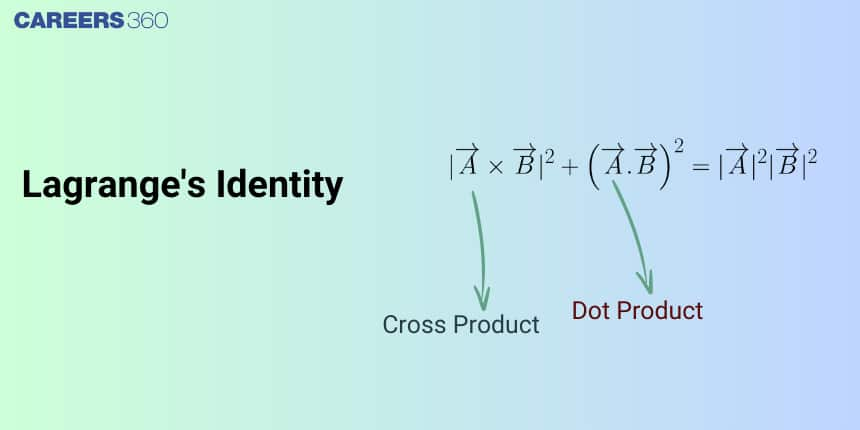
Example 2: If $\vec{a}$ and $\vec{b}$ are two vectors such that $|\vec{a}|=3$ and $|\vec{b}|=2$ then $|\vec{a} * \vec{b}|^2+(\vec{a} \cdot \vec{b})^2$ equals
Solution: We know that Lagrange's identity -

$\big|\vec{a} \times \vec{b}\big|^2 = |\vec{a}|^2 |\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2$

Here, $\vec{a}$ and $\vec{b}$ are two vectors.

$|\vec{a} \times \vec{b}|^2 + (\vec{a} \cdot \vec{b})^2 = |\vec{a}|^2 |\vec{b}|^2 \sin^2 \theta + |\vec{a}|^2 |\vec{b}|^2 \cos^2 \theta$

$= |\vec{a}|^2 |\vec{b}|^2 = 9 \times 4 = 36$

Hence, the answer is 36

Example 3: $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ are vectors then $(\vec{a} \times \vec{b}) \times(\vec{c} \times \vec{d})$ equals:
Solution:

$(\vec{a} \times \vec{b}) \times (\vec{c} \times \vec{d}) = - \left[ (\vec{c} \times \vec{d}) \times (\vec{a} \times \vec{b}) \right]$

$= - \left[ ((\vec{c} \times \vec{d}) \cdot \vec{b}) \vec{a} - ((\vec{c} \times \vec{d}) \cdot \vec{a}) \vec{b} \right]$

$= [\vec{a}, \vec{c}, \vec{d}] \vec{b} - [\vec{b}, \vec{c}, \vec{d}] \vec{a}$

$\text{Hence, the answer is} \quad [\vec{a}, \vec{c}, \vec{d}] \vec{b} - [\vec{b}, \vec{c}, \vec{d}] \vec{a}$

Example 4: $\vec{a}$ and $\vec{b}$ are vectors such that $\left|\begin{array}{ll}\vec{a} \cdot \vec{a} & \vec{a} \cdot \vec{b} \\ \vec{a} \cdot \vec{b} & \vec{b} \cdot \vec{b}\end{array}\right|=16 \quad|\vec{a} \times \vec{b}|_{\text {equals }}$
Solution:

$\left|\begin{array}{ll}\vec{a} \cdot \vec{a} & \vec{a} \cdot \vec{b} \\ \vec{a} \cdot \vec{b} & \vec{b} \cdot \vec{b}\end{array}\right|=16$

$\Rightarrow |\vec{a}|^2 |\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2 = 16$

$\Rightarrow |\vec{a} \times \vec{b}|^2 = 16 \Rightarrow |\vec{a} \times \vec{b}| = 4$
Hence, the answer is 4

Example 5: Let $\vec{a}, \vec{b}, \vec{c}$ are three non-coplanar vectors, such that $[\vec{a} \vec{b} \vec{c}]=2$ the reciprocal system of vectors will form a parallelepiped with volume:
Solution: Reciprocal System of Vectors -

$\vec{a}^{,\prime} = \dfrac{ \vec{b} \times \vec{c} }{ [\vec{a}\ \vec{b}\ \vec{c}] }$

$\vec{b}^{,\prime} = \dfrac{ \vec{c} \times \vec{a} }{ [\vec{a}\ \vec{b}\ \vec{c}] }$

$\vec{c}^{,\prime} = \dfrac{ \vec{a} \times \vec{b} }{ [\vec{a}\ \vec{b}\ \vec{c}] }$

$\vec{a},\ \vec{b},\ \vec{c}\ \text{are three vectors}$

$\text{i.e.}\ \dfrac{ \vec{b} \times \vec{c} }{2 },\ \dfrac{ \vec{c} \times \vec{a} }{2 },\ \dfrac{ \vec{a} \times \vec{b} }{2 }$

$\text{The volume of parallelepiped} = \left| \left[ \frac{ \vec{b} \times \vec{c} }{2 },, \frac{ \vec{c} \times \vec{a} }{2 },, \frac{ \vec{a} \times \vec{b} }{2 } \right] \right|$

$= \left| \frac{1}{8} \left[ \vec{b} \times \vec{c},, \vec{c} \times \vec{a},, \vec{a} \times \vec{b} \right] \right| = \frac{1}{8} \left( [ \vec{a}\ \vec{b}\ \vec{c} ] \right)^2 $

$= \frac{1}{8} \times 4 = \frac{1}{2}$

$\text{Hence, the answer is}\ \frac{1}{2}$

List of topics related to Lagrange’s Identity

Explore the foundational vector concepts essential to understanding and applying Lagrange’s Identity. This list includes key topics like linear combination of vectors, types of vectors, direction cosines and direction ratios of a line, dot and cross product operations, section formula, and the geometrical interpretation of vector products.

• Linear Combination of Vectors

• Types of Vectors

• Direction Cosines & Direction Ratios Of A Line

• Dot Product of Two Vectors

• Cross Product

• Section Formula

• Geometrical Interpretation of the Product of Vectors

NCERT Resources

Access structured NCERT resources to strengthen your understanding of Lagrange’s Identity and vector algebra. This section covers Class 12 Maths Chapter 10 materials, including NCERT notes, detailed solutions, and exemplar problem sets. These resources align with the CBSE curriculum and help reinforce concepts like dot and cross products, linear combinations, and Lagrange’s identity vector formulation.

NCERT Notes for Class 12 Maths Chapter 10 - Vector Algebra

NCERT Solutions for Class 12 Maths Chapter 10 - Vector Algebra

NCERT Exemplar Solutions for Class 12 Maths Chapter 10 - Vector Algebra

Practice Questions based on Lagrange’s Identity

Strengthen your grasp of vector algebra and Lagrange’s Identity with topic-wise multiple-choice questions. This section includes MCQs on key concepts such as dot and cross products, linear combination of vectors, direction cosines and ratios, scalar triple product, and vector operations. Each question is designed to test conceptual clarity and application skills relevant for board exams and competitive entrance tests.

Lagrange's Identity - Practice Question MCQ

You can practice the following topics related to vector algebra: