What is biconvex lens/give the biconvex definition/biconvex meaning.

The term ‘biconvex’ itself explains that the biconvex lens is made up of two convex lenses.

Who discovered lens and convex lens?

The lens is discovered by George Rober Carruthers and Pal Rudolph and also the Convex lens is discovered by Roger Bacon

What is biconvex shape?

Biconvex is curved at both sides.

Write down the difference between the convex lens and convex mirror.

There are two major differences between the convex lens and convex mirrors, the transparency of the convex mirror is opaque and the transparency of the convex lens is transparent. The reflection of light is the result of the convex mirror and the refraction of light is the result of a concave lens.

Write down the difference between the convex lens and concave lens.

The centre of the convex lens is thicker whereas the centre of the concave lens is thinner. For the convex lens, the edges are thinner whereas the edges of the concave lens are thicker. The convex lens is known as a converging lens as it converges the incident ray and the concave lens are known as a diverging lens as it diverges the incident ray. These are the major differences between the convex lens and concave lens.

What is double convex lens?

Lenses having the same radius of curvature on both the sides are called double convex lens.

Difference between the biconvex lens and double convex lens.

There is no big difference between the double convex and biconvex lens, as they are made up of the same type of lens. The only difference is the radius of curvature of the lenses used is different in the double convex lens whereas the radius of curvature of the lenses used is the same in the biconvex lens.

Give some uses and application of biconvex lens.

These lenses are used as condensing or magnifying lens Objectives or magnifiers are made up of the biconvex lens Imaging systems like microscope, telescope, monocular, binoculars, camera and so on utilizes the biconvex lens in their manufactures. The biconvex lens is used to produce the virtual image which is used to clear the defects in the human eye and real image in some photographic films and is also used in optical sensors. The biconvex lens is used in the burning glass. The biconvex lens also plays an important role in image relays and is used in different optical industries.

List some of the properties of biconvex lens

The focal length of the biconvex lens is found to be in the positive axis The focal length of the biconvex lens is found to be very shorter than the concave lens The incident light converges in the biconvex lens. The output images are found to be both real and virtual images, it depends on the focal length of the incident light beam. To minimize the spherical aberration, coma and distortion, the biconvex lens is used in practice. The biconvex lens is symmetrical as it is made up of two exact convex lenses with the same radii of curvature and they have an equal radius on both sides.

What is a biconvex lens?

A biconvex lens is a type of optical lens that is curved outward on both sides. It is thicker in the middle and thinner at the edges, causing light rays to converge to a focal point when passing through it.

What is the focal point of a biconvex lens?

The focal point is the point where parallel light rays converge after passing through the lens. It is located on the principal axis of the lens, and its distance from the lens center is called the focal length.

What is the difference between a real and a virtual image formed by a biconvex lens?

A real image is formed when light rays actually converge at a point and can be projected on a screen. A virtual image is formed when light rays appear to diverge from a point but do not actually meet there, and cannot be projected on a screen.

What is magnification in the context of biconvex lenses?

Magnification is the ratio of image size to object size. For a biconvex lens, it can be calculated as the ratio of image distance to object distance (v/u) or as the negative ratio of image height to object height (-hi/ho).

What is the thin lens formula, and how is it applied to biconvex lenses?

The thin lens formula is 1/f = 1/u + 1/v, where f is the focal length, u is the object distance, and v is the image distance. This formula helps calculate the relationship between object and image positions for biconvex lenses.

How does a biconvex lens differ from other types of lenses?

A biconvex lens is convex on both sides, while other lenses may be concave on one or both sides. This shape allows biconvex lenses to converge light rays, unlike concave lenses which diverge light.

How does the curvature of a biconvex lens affect its focal length?

The greater the curvature of the lens surfaces, the shorter the focal length. A more curved lens will bend light rays more sharply, causing them to converge closer to the lens.

Can a biconvex lens produce both real and virtual images?

Yes, a biconvex lens can produce both real and virtual images depending on the object's position relative to the focal point. Objects beyond the focal point produce real, inverted images, while objects between the focal point and the lens produce virtual, upright images.

How does the position of an object affect the image formed by a biconvex lens?

The image characteristics (size, orientation, and position) change based on the object's position relative to the focal point. As the object moves closer to the lens, the image generally becomes larger and moves farther away from the lens.

How do you determine if an image formed by a biconvex lens is magnified or diminished?

If the magnification is greater than 1, the image is magnified. If it's less than 1, the image is diminished. This can be determined by comparing the image size to the object size or by calculating the magnification using the formula.

How does a biconvex lens correct farsightedness (hyperopia)?

A biconvex lens helps correct farsightedness by converging light rays before they reach the eye. This compensates for the eye's inability to focus nearby objects on the retina, allowing clear vision of close objects.

How can chromatic aberration be minimized in biconvex lenses?

Chromatic aberration can be reduced by using achromatic doublets (combining two lenses of different materials) or by using low-dispersion glass. These methods help different wavelengths of light converge more closely to the same point.

How does the thickness of a biconvex lens affect its optical properties?

Thicker lenses generally have shorter focal lengths and greater refractive power. However, very thick lenses can introduce more aberrations and are less accurately described by the thin lens approximation.

How does the shape of a biconvex lens affect its ability to form images?

The curvature of both surfaces affects how the lens bends light. Symmetrical biconvex lenses (same curvature on both sides) minimize certain aberrations, while asymmetrical designs can be optimized for specific applications.

What is the difference between a biconvex lens and a plano-convex lens?

A biconvex lens is curved outward on both sides, while a plano-convex lens is flat on one side and curved outward on the other. Biconvex lenses generally have shorter focal lengths and are more symmetrical in their optical properties.

How does a biconvex lens form an image of an infinitely distant object?

For an infinitely distant object, incoming light rays are essentially parallel. A biconvex lens focuses these rays to a point at its focal length, forming a real, inverted image at the focal point.

What is the relationship between object distance and image distance for a biconvex lens?

As the object moves closer to the lens, the image generally moves farther away. This relationship is described by the thin lens equation and results in changes to image size and type (real or virtual).

What happens to the image formed by a biconvex lens if half of the lens is covered?

If half of a biconvex lens is covered, the entire image will still form, but it will be dimmer. This is because each point on the object sends light to every part of the lens, so blocking part of the lens only reduces the light intensity.

How do biconvex lenses function in a compound microscope?

In a compound microscope, the objective lens (usually biconvex) forms a real, magnified image of the specimen. The eyepiece lens (also typically biconvex) further magnifies this image, creating a highly enlarged virtual image for the observer.

How does the image formation in a biconvex lens differ from that in a plane mirror?

A biconvex lens can form both real and virtual images, and these images can be magnified or diminished. A plane mirror always forms virtual, upright images that are the same size as the object.

How does the index of refraction of the surrounding medium affect the behavior of a biconvex lens?

If the surrounding medium has a higher refractive index (e.g., water instead of air), the lens's ability to bend light decreases. This effectively increases the focal length and decreases the lens's power.

How does a biconvex lens in a camera compare to the lens in a human eye?

Both function as converging lenses, forming real, inverted images. However, a camera lens has a fixed focal length and focuses by moving, while the eye's lens changes shape to focus (accommodation).

How does a biconvex lens behave differently when immersed in a liquid compared to air?

When immersed in a liquid with a refractive index closer to that of the lens material, the lens's ability to bend light decreases. This results in a longer focal length and reduced power, as the difference in refractive indices between the lens and its surroundings is smaller.

How does the concept of wavefronts apply to the behavior of light in a biconvex lens?

A biconvex lens transforms plane wavefronts (from distant objects) into converging spherical wavefronts. This change in wavefront shape is what allows the lens to form images by bringing light rays to a focus.

How does the thickness of a biconvex lens affect its ability to approximate a thin lens?

As a lens becomes thicker relative to its focal length and radii of curvature, it deviates more from thin lens behavior. Thick lenses require more complex equations that account for the distance between the two refracting surfaces.

What is the role of a biconvex lens in a simple magnifying glass?

In a magnifying glass, the biconvex lens is used to create an enlarged, virtual image of a nearby object. The object is placed within the focal length of the lens, causing the emerging rays to diverge as if from a larger virtual image.

What is the relationship between the object and image distances when an object is placed at the focal point of a biconvex lens?

When an object is placed exactly at the focal point of a biconvex lens, the image forms at infinity. This means the emerging rays are parallel and do not converge to form an image at any finite distance.

What is the significance of the lens equation in understanding the behavior of biconvex lenses?

The lens equation (1/f = 1/u + 1/v) provides a mathematical relationship between object distance, image distance, and focal length. It's crucial for predicting image characteristics and understanding how changes in object position affect the image.

How does a biconvex lens contribute to the formation of a real image in a film camera?

In a film camera, the biconvex lens forms a real, inverted image on the film plane. It converges light rays from each point on the object to corresponding points on the film, creating a focused image when the film is at the correct distance from the lens.

What is the relationship between the focal length of a biconvex lens and its ability to resolve fine details?

Lenses with shorter focal lengths generally have a higher resolving power, meaning they can distinguish finer details. This is because shorter focal lengths allow for larger numerical apertures, which improve resolution according to the diffraction limit.

How does the principle of reversibility apply to light paths in a biconvex lens system?

The principle of reversibility states that light can travel along the same path in either direction. In a biconvex lens system, this means that if an object and its image are swapped in position, the new image will form where the original object was located.

What is the significance of the 2F point in a biconvex lens system?

The 2F point is twice the focal length from the lens center. When an object is placed at 2F, its image will also form at 2F on the opposite side of the lens, with the same size as the object but inverted.

What is chromatic aberration, and how does it affect biconvex lenses?

Chromatic aberration is the failure of a lens to focus all colors to the same point. In biconvex lenses, it causes different wavelengths of light to focus at slightly different points, resulting in colored fringes around images.

What is spherical aberration in biconvex lenses?

Spherical aberration occurs when light rays passing through the edges of a lens are focused at a different point than rays passing through the center. This results in a slightly blurred image, especially for off-axis points.

Biconvex Lens - Properties, Formula, Uses, FAQs

Vishal kumarUpdated on 02 Jul 2025, 04:44 PM IST

The biconvex lens is one of the lenses which is made up of two different convex surfaces that form a spherical shape. This lens has some radius of curvature. The other term that represents the biconvex Lens is the convex-convex lens. In this article, let us see about the biconvex lens, biconvex mirrors, double convex lens, and the difference between the biconcave lens and a biconvex lens. This kind of biconvex lens is very simple but is used in various fields and contains a lot of applications. For example, the biconvex lens has more applications in the field of laser beams, optical instruments, quality imaging and so on.

This Story also Contains

What are the Terms Used in the Biconvex Lens?
The Usage of Biconvex Lens in the Human Eye
Properties of Biconvex lens
The Formula for Biconvex Lens
Making of the Biconvex Lens in the Home
Uses and Applications of the Biconvex Lens

Biconvex Lens

What are the Terms Used in the Biconvex Lens?

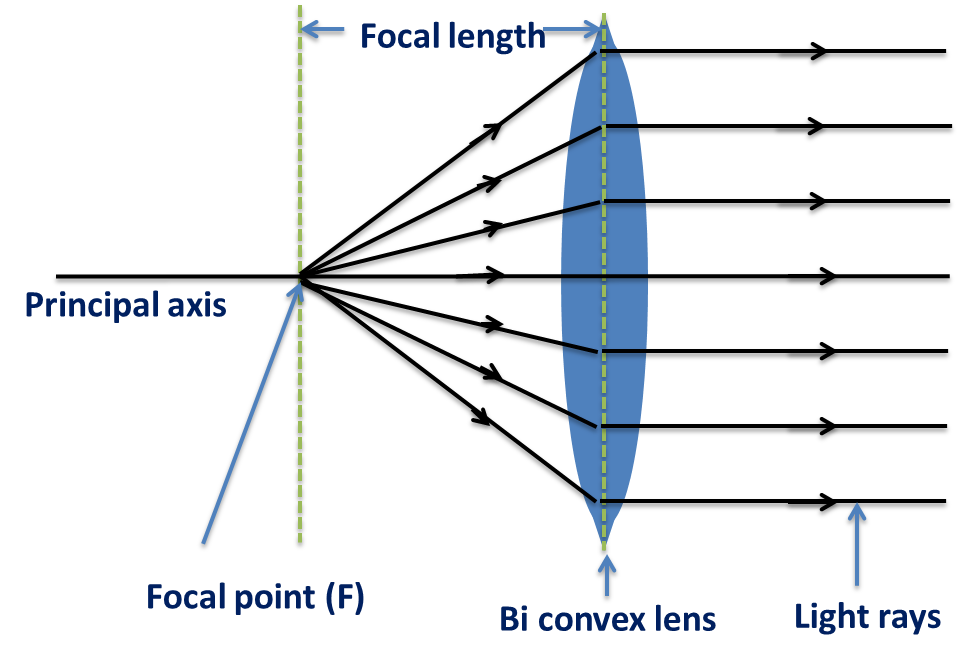
Focus:

In the biconvex lens, a collimated light beam or a light beam which is accurately parallel to each other is allowed to pass through the biconvex lens and the light beams converge at a particular spot. This spot can be defined as the focus.

Optical Centre:

The centre of the lens is known as the optical centre.

Focal length:

The length or distance between the centre of the lens and the focus can be called the focal length.

Principal axis:

The axis or the line that cuts the convex lens horizontally and passes through the optical center of the lens, is called the principal axis.

The Usage of Biconvex Lens in the Human Eye

The best example of the biconvex lens is the eyes lens used for the rectification of human eye defects. In the working mechanism of the human eye, when the light rays which come from an object or target enter the eye, bend sharp and fall on the focus of the retina. The light beam which is coming from a large distance needs only less refraction. For the higher convex lens, the refraction is greater.

Structure and Functions of the Human Eye with Diagram

Properties of Biconvex lens

Some basic properties of the biconvex lens are listed below:

The focal length of the biconvex lens is found to be on the positive axis
The focal length of the biconvex lens is found to be much shorter than the concave lens
The incident light converges in the biconvex lens.
The output images are found to be both real and virtual images, it depends on the length of the object from the lens.
To minimize the spherical aberration, coma and distortion, the biconvex lens is used in practice.
The biconvex lens is symmetrical as it is made up of two exact convex lenses with the same radii of curvature and they have an equal radius on both sides.
The positive conjugate ratio ranges from 0.2 to 5.

focal point and principle axis of biconvex lens is shown in the image

Also read -

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

The Formula for Biconvex Lens

We know the formula for focal length is

$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

Where f represents the focal length of the biconvex lens

u represents the object distance from the biconvex lens

v represents the image distance from the biconvex lens

The refraction of the spherical surface formula is given as

$\frac{1}{v}-\frac{1}{u}=\left(\frac{\mu_2}{\mu_1}-1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]$

Where 1 and 2 are the refractive indexes of the medium

R1 and R2 are the radii of curvature of lens 1 and lens 2

Related Topics,

Making of the Biconvex Lens in the Home

Take and cut the cardboard with a diameter of 2.5 centimetres.
Place the cardboard on the water bottle and make its shape. Now cut the two different circles from the water bottle of the same radius of cardboard by using the scissors.
Paste the two circles such that the centre of the lens is not stuck together.
Now, this circle looks like a partial biconvex lens.

Uses and Applications of the Biconvex Lens

These lenses are used as condensing or magnifying lens
Objectives or magnifiers are made up of the biconvex lens
Imaging systems like microscopes, telescopes, monoculars, binoculars, cameras and so on utilize the biconvex lens in their manufactures.
The biconvex lens is used in the burning glass.
The biconvex lens also plays an important role in image relays and is used in different optical industries.
The biconvex lens is used to produce the virtual image which is used to clear the defects in the human eye and real image in some photographic films and is also used in optical sensors.

In this article, we saw a detailed explanation of the biconvex lens, its working and its uses. Let us discuss some frequently asked questions asked in class 10, class 11 and class 12 related to the biconvex lens.
Also, check-

Frequently Asked Questions (FAQs)

Q: How does the concept of depth of field relate to the use of biconvex lenses in imaging systems?

Depth of field refers to the range of distances over which objects appear acceptably sharp in an image. For biconvex lenses, a smaller aperture (higher f-number) increases the depth of field, allowing a greater range of object distances to be in focus simultaneously.

Q: What is the difference between longitudinal and lateral magnification in the context of biconvex lenses?

Longitudinal magnification refers to the ratio of image distance to object distance, while lateral magnification is the ratio of image size to object size. For a thin lens, lateral magnification is equal to the negative of longitudinal magnification.

Q: What is the significance of the optical center in a biconvex lens?

The optical center is a point within the lens through which light rays pass undeviated. It's crucial for ray diagrams and calculations, as it's often treated as the point from which distances are measured in lens equations.

Q: What is the refractive index, and how does it relate to biconvex lenses?

The refractive index is a measure of how much a material slows down light. Lenses with higher refractive indices bend light more sharply, resulting in shorter focal lengths for the same lens curvature.

Q: How does the f-number (f-stop) relate to biconvex lenses?

The f-number is the ratio of the lens's focal length to its diameter. It affects the amount of light passing through the lens and the depth of field. Lower f-numbers allow more light but have a shallower depth of field.

Q: What is the principal axis of a biconvex lens?

The principal axis is an imaginary line that passes through the center of the lens perpendicular to its surfaces. It's the line along which the optical center and focal points lie.

Q: How does the power of a biconvex lens relate to its focal length?

The power of a lens, measured in diopters, is the reciprocal of its focal length in meters (P = 1/f). A shorter focal length means a higher power, indicating a stronger ability to bend light.

Q: What is the difference between a converging and diverging lens, and which category does a biconvex lens fall into?

A converging lens brings parallel light rays to a focus, while a diverging lens spreads them apart. A biconvex lens is a converging lens, as it causes parallel light rays to converge to a focal point.

Q: What is the thin lens approximation, and when is it applicable to biconvex lenses?

The thin lens approximation assumes that the thickness of the lens is negligible compared to its focal length and the radii of curvature of its surfaces. It's applicable when the lens is thin relative to these dimensions and simplifies calculations.

Q: What is the difference between the principal focus and the optical center of a biconvex lens?

The principal focus is the point where parallel rays converge after passing through the lens, while the optical center is a point within the lens through which light passes without deviation. They are distinct points with different roles in image formation.

Articles

Top 6 Career Options after BAF - Eligibility, Salary

Sep 06, 2025

Gujarat Paramedical Merit List 2025 Revised (Out): Download PDF Rank List

Sep 04, 2025

How Online Degree Exams are Conducted in India?

Sep 01, 2025

UPTAC Cutoff 2025 Round 3 (Out) - AKTU Opening and Closing Rank

Aug 23, 2025