Mirror Equation - Definition, Formula, Applications, FAQs

Spherical Mirrors: Concave and Convex Mirror

A spherical mirror is a mirror whose reflecting surface is a part of a hollow sphere. The reflecting surface can be either curved inward or outward.

Concave Mirror:

• A concave mirror has its reflecting surface curved inward, like the inside of a bowl.
• It is also called a converging mirror because it focuses parallel rays of light to a single point called the focus.
• It is used in shaving mirrors, headlights, torches, and solar furnaces.

Convex Mirror:

• A convex mirror has its reflecting surface curved outward.
• It is called a diverging mirror because it spreads parallel rays of light outward.
• It is used as a rear-view mirror in vehicles as it gives a wider field of view.

What is Mirror Equation?

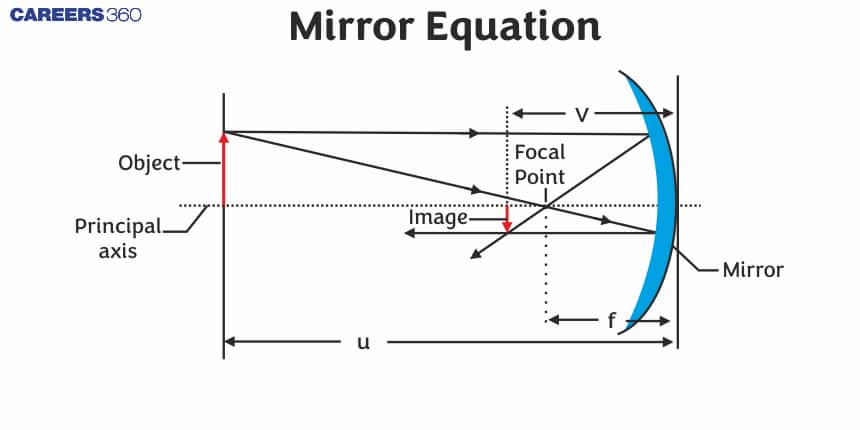
A mirror is an optical device that reflects light and forms images. The mirror equation is a mathematical relationship that connects the object distance $(\mathbf{u})$, image distance $(\mathbf{v})$, and the focal length $(\mathbf{f})$ of a mirror. It is valid for both concave and convex mirrors.

The mirror equation is expressed as:

$
\frac{1}{f}=\frac{1}{u}+\frac{1}{v}
$

Where:

• $f=$ focal length of the mirror
• $u=$ distance of the object from the mirror (measured from the pole of the mirror)
• $v=$ distance of the image from the mirror

Sign Convention for Mirror

The mirror equation adheres to the following sign conventions:

1. The mirror's principal axis is drawn along the x-axis of the rectangular coordinate system, and its pole is drawn as the origin.

2 . The object is taken from the left side of the mirror, implying that light is incident on the mirror from the left.

3. All distances parallel to the mirror's major axis are measured from the mirror's pole.

4. Distances measured in the direction of incident light are considered positive.

5. Negative distances are those measured in the opposite direction of the incident light.

6. All heights measured upwards and perpendicular to the mirror's primary axis are considered positive.

7. The heights measured downwards and perpendicular to the mirror's major axis are considered negative.

As a result, the focal length of a concave mirror equation is negative, while the focal length of a convex mirror equation is positive. In addition, the object distance and object height are treated as negative and positive values, respectively.

Concave Mirror Equation

For concave mirrors, the mirror equation is given as,

$$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$$

where,

• $v$ is the image distance
• $u$ is the object distance
• $f$ is the focal length of the mirror

The effect of an object's position relative to the focal point of a mirror equation on the picture (concave)

1. When anything is placed between the focus point and the mirror.

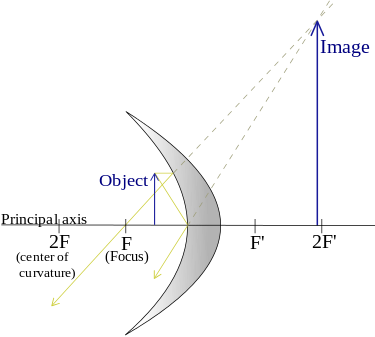
The nature of the image formula produced will be Virtual, Upright, and magnified.

2. When an object is present at the focal point of the mirror.

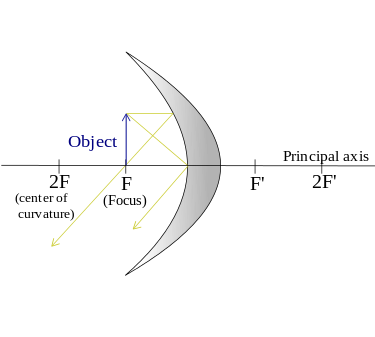
Because the rays due to the reflection of light are parallel and never intersect, no image formula is generated.

The picture distance approaches infinity as S approaches F, and the image formula can be actual or virtual, upright or inverted, depending on whether S approaches F from the left or right side.

3. When an object is put between the focus and the center of the curvature.

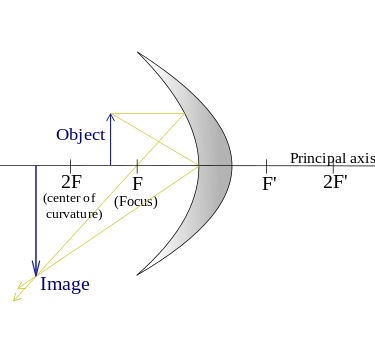
The resulting image will be a true/real image, Reversed (vertically) and enlarged (larger).

4. When an object is in the center of the curve.

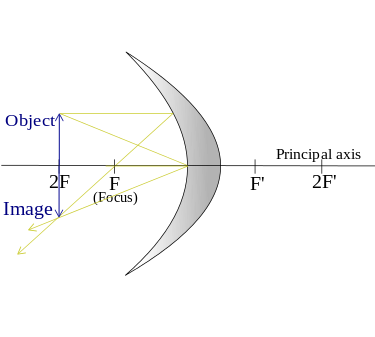
The resulting image will be a real image inverted (vertically), the same size.

At the center of the curvature, an image is generated.

5. When an object extends beyond the center of curvature.

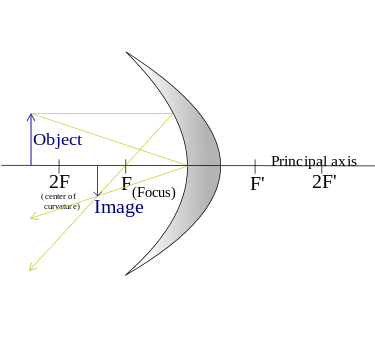
The resulting image will be a Real image, Reversed (vertically), Reduced (smaller).

As the object's distance grows, the picture approaches the focal point asymptotically.

As the image approaches F, the image size approaches 0 in the limit where S approaches infinity.

Convex Mirror Equation

The mirror formula for spherical mirrors like convex mirrors is the same as the general mirror equation,

$
\frac{1}{f}=\frac{1}{u}+\frac{1}{v}
$

where,

• $v$ is the image distance
• $u$ is the object distance
• $f$ is the focal length of the mirror

The effect of an object's position relative to the focal point of a mirror equation on the picture (convex)

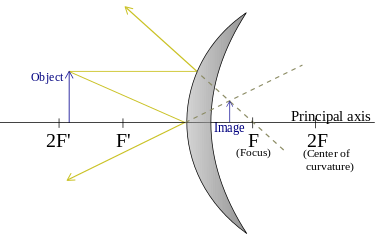
A convex mirror's image is always virtual (rays do not travel through the picture; their extensions do, as in a regular mirror), reduced as well as upright as the object gets closer to the mirror, the image grows larger until it is roughly the size of the object when it reaches the mirror. Convex mirrors are highly useful because, because everything seems smaller in the mirror, they cover a greater field of vision than a conventional plane mirror, making them ideal for seeing cars behind a driver's car on the road, viewing a larger area for surveillance, and so on.

Mirror Equation Uses

The Mirror equation is used in the following ways:

1. When the object distance and the focal length of the mirror equation are known, the mirror equation can be used to determine the image distance.
2. When we know the image distance and the focal length of the mirror, we can use the mirror equation to calculate the object distance.
3. The mirror equation allows us to calculate the focal length of the mirror equation simply by knowing the distance between the item and the image it generates.
4. When we use the mirror equation in conjunction with the magnification equation, we can obtain the value of either the image height or the object height when the other is specified.

Example of Mirror Equation

Problem:
A concave mirror has a focal length of 15 cm . An object is placed 30 cm in front of the mirror. Find the image distance.

Solution:

Mirror equation:

$
\begin{gathered}
\frac{1}{f}=\frac{1}{u}+\frac{1}{v} \\
\frac{1}{15}=\frac{1}{30}+\frac{1}{v} \quad \Rightarrow \quad \frac{1}{v}=\frac{1}{30} \quad \Rightarrow \quad v=30 \mathrm{~cm}
\end{gathered}
$

Answer: The image is $\mathbf{3 0 ~ c m}$ in front of the mirror, real and inverted.
Magnification:

$
m=-\frac{v}{u}=-1
$

The image is of the same size but inverted.

Related Topics,

• Plane Mirrors
• The Lens Maker’s Formula
• Power of a Lens Ray Optics
• Uses of Convex Lens