What’s the optician/optical formula and why is it called so?

The optician/optical formula may be a relation between the focal distance, the index of refraction of constituent material, and therefore the radii of curvature of the spherical surfaces of a lens. The refractive power (inverse of focal length) is often computed from this formula. Lens manufacturers use this reference to construct a lens of a specific power.

What is Limitations of Lens Maker’s Formula?

The lens must be thin. This is often because the separation between the 2 refracting surfaces also will be small. The medium on either side of the lens must be an equivalent

Why is that the thin lens approximation used?

A light ray gets refracted twice (at two surfaces) while passing through a lens. To avoid this birefringence, thin lenses are considered. This approximation is valid when the thickness is extremely small compared to the radii of curvature. The approximation works well during this range and it simplifies the computations tons.

What is mean by lens?

The lens is a transparent refractive medium which is built by joining two surfaces with either 2 curved surfaces or a curved and a plane surface.

Give the definition radius of curvature of the lens.

The radius of the sphere of which the surface of the lens may be a part is named the radius of curvature of the lens. A lens has two radii of curvatures.

What is the Lens Maker's Formula?

The Lens Maker's Formula is an equation that relates the focal length of a thin lens to its refractive index and the radii of curvature of its surfaces. It is given by 1/f = (n-1)(1/R1 - 1/R2), where f is the focal length, n is the refractive index of the lens material, and R1 and R2 are the radii of curvature of the two surfaces of the lens.

Why is the Lens Maker's Formula important in optics?

The Lens Maker's Formula is crucial in optics because it allows us to design and manufacture lenses with specific focal lengths. It helps in understanding how the shape and material of a lens affect its focusing properties, which is essential for creating optical instruments like cameras, microscopes, and telescopes.

How does the refractive index affect the focal length in the Lens Maker's Formula?

In the Lens Maker's Formula, the refractive index (n) appears as (n-1). A higher refractive index results in a shorter focal length for the same lens shape. This means that lenses made of materials with higher refractive indices can bend light more strongly, allowing for thinner lenses with the same focusing power.

What happens to the focal length if the radii of curvature (R1 and R2) are equal in magnitude but opposite in sign?

If R1 = -R2, the lens is symmetrical (equiconvex or equiconcave). In this case, the Lens Maker's Formula simplifies to 1/f = 2(n-1)/R, where R is the magnitude of either radius. This results in a shorter focal length compared to an asymmetrical lens with the same average curvature.

Can the Lens Maker's Formula be applied to thick lenses?

The Lens Maker's Formula is specifically derived for thin lenses, where the thickness is negligible compared to the radii of curvature. For thick lenses, a modified version of the formula or more complex optical calculations are required to accurately determine the focal length.

How does the sign convention work in the Lens Maker's Formula?

In the Lens Maker's Formula, the sign convention is crucial. For a convex surface facing the incident light, the radius is positive. For a concave surface facing the incident light, the radius is negative. The focal length is positive for converging lenses and negative for diverging lenses.

What does a negative focal length in the Lens Maker's Formula indicate?

A negative focal length indicates that the lens is diverging (concave). This means that parallel rays of light passing through the lens will diverge as if they originated from a virtual focal point behind the lens.

How does the Lens Maker's Formula relate to the power of a lens?

The power of a lens (P) is the reciprocal of its focal length (f) in meters. Therefore, P = 1/f. The Lens Maker's Formula directly gives us 1/f, which is the power of the lens in diopters when f is in meters.

Can the Lens Maker's Formula be used for lenses in any medium?

The standard form of the Lens Maker's Formula assumes the lens is in air. For lenses in other media, the formula needs to be modified to use the relative refractive index (the ratio of the lens material's refractive index to that of the surrounding medium) instead of the absolute refractive index.

How does the Lens Maker's Formula account for different lens shapes?

The formula accounts for different lens shapes through the radii of curvature (R1 and R2). For example, a plano-convex lens has one flat surface (infinite radius) and one curved surface. A biconvex lens has two positive radii, while a biconcave lens has two negative radii.

What happens when one of the radii in the Lens Maker's Formula approaches infinity?

When one radius approaches infinity, that surface becomes flat. This results in a plano-convex or plano-concave lens. The term 1/R for the flat surface becomes zero, simplifying the formula to 1/f = (n-1)/R, where R is the radius of the curved surface.

How does the Lens Maker's Formula relate to the thin lens approximation?

The Lens Maker's Formula is derived using the thin lens approximation, which assumes that the thickness of the lens is negligible compared to its radii of curvature. This approximation allows us to treat the lens as a single refracting surface, simplifying the calculations.

Can the Lens Maker's Formula be used to calculate the focal length of a compound lens system?

The Lens Maker's Formula applies to single lenses. For a compound lens system, you would need to calculate the focal length of each lens separately and then use the thin lens combination formulas to determine the overall focal length of the system.

How does changing the wavelength of light affect the results from the Lens Maker's Formula?

The Lens Maker's Formula doesn't explicitly include wavelength, but it's implicitly present in the refractive index (n). Different wavelengths of light have different refractive indices in a material, a phenomenon known as dispersion. This means the focal length calculated will vary slightly for different colors of light.

What is the relationship between the Lens Maker's Formula and chromatic aberration?

Chromatic aberration occurs because different wavelengths of light have different refractive indices in a material. The Lens Maker's Formula shows that the focal length depends on the refractive index, so different wavelengths will focus at slightly different points, causing chromatic aberration.

How does the Lens Maker's Formula relate to the concept of optical power?

The Lens Maker's Formula directly gives the reciprocal of the focal length (1/f), which is the definition of optical power in diopters when f is in meters. This shows that the optical power of a lens is determined by its shape (radii of curvature) and material (refractive index).

Can the Lens Maker's Formula be used to design achromatic lenses?

While the Lens Maker's Formula itself doesn't directly address achromatic design, understanding it is crucial for creating achromatic lenses. By combining lenses with different refractive indices and shapes, calculated using the formula, it's possible to design lens systems that minimize chromatic aberration.

How does the Lens Maker's Formula account for astigmatism in lenses?

The standard Lens Maker's Formula assumes spherical surfaces and doesn't account for astigmatism. For lenses with astigmatism, where the radii of curvature are different in different planes, more complex formulas are needed that consider these variations.

What assumptions are made in deriving the Lens Maker's Formula?

The main assumptions in deriving the Lens Maker's Formula are: 1) The lens is thin (thickness is negligible compared to radii of curvature), 2) The lens material is homogeneous, 3) The lens surfaces are spherical, 4) Paraxial approximation is valid (rays are close to and nearly parallel with the optical axis), and 5) The lens is in air.

How does the Lens Maker's Formula relate to the concept of vergence in optics?

Vergence is the reciprocal of distance and is measured in diopters. The Lens Maker's Formula gives 1/f, which is the vergence of light after passing through the lens when incident light is parallel (vergence = 0). This shows how the lens changes the vergence of light.

Can the Lens Maker's Formula be used for mirrors?

The Lens Maker's Formula is specifically for lenses. For mirrors, a simpler formula is used: 1/f = 1/(2R), where R is the radius of curvature of the mirror. This is because mirrors reflect light rather than refracting it, so the refractive index doesn't play a role.

How does the Lens Maker's Formula relate to the concept of focal power addition in optometry?

In optometry, when adding the power of lenses (like in bifocals), we add the reciprocals of focal lengths (1/f). The Lens Maker's Formula gives us 1/f directly, making it easier to calculate combined lens powers in optical systems or corrective lenses.

What happens to the focal length in the Lens Maker's Formula if the refractive index of the lens material equals that of the surrounding medium?

If the refractive index of the lens equals that of the surrounding medium, (n-1) becomes zero in the Lens Maker's Formula. This results in an infinite focal length, meaning the lens has no focusing power. This is why objects are harder to see in water - the difference in refractive indices is reduced.

How does the Lens Maker's Formula help in understanding the concept of diopters in vision correction?

The Lens Maker's Formula directly gives the power of a lens in diopters when the focal length is in meters. This helps in understanding how the shape and material of a lens contribute to its corrective power in vision, and why certain lens designs are used for specific vision problems.

Can the Lens Maker's Formula be applied to gradient-index lenses?

The standard Lens Maker's Formula assumes a uniform refractive index throughout the lens. For gradient-index lenses, where the refractive index varies within the lens, more complex formulas that account for this variation are required.

How can the Lens Maker's Formula be used to design a lens with a specific focal length?

To design a lens with a specific focal length, you can rearrange the Lens Maker's Formula to solve for one of the radii of curvature, given the desired focal length, refractive index, and one radius. This allows lens designers to create lenses with precise focusing properties for various applications.

What is the significance of the (n-1) term in the Lens Maker's Formula?

The (n-1) term in the Lens Maker's Formula represents the optical power of the lens material relative to air. It shows that the focusing power of a lens depends not just on its shape, but on how much the material bends light compared to the surrounding medium (usually air).

How does the Lens Maker's Formula help in understanding the concept of principal planes in thick lenses?

While the Lens Maker's Formula is for thin lenses, understanding it is crucial for grasping the concept of principal planes in thick lenses. The formula assumes all refraction occurs at a single plane, which is analogous to how principal planes simplify calculations for thick lenses by treating them as equivalent thin lenses.

Can the Lens Maker's Formula be used to calculate the focal length of a Fresnel lens?

The Lens Maker's Formula cannot be directly applied to Fresnel lenses, which consist of a series of concentric grooves. However, understanding the formula helps in designing Fresnel lenses, as each groove acts like a small section of a conventional lens, collectively approximating the focusing power of a much thicker lens.

How does the Lens Maker's Formula relate to the concept of dioptric power matrices in astigmatic lenses?

While the Lens Maker's Formula is for spherical lenses, it forms the basis for understanding more complex formulations like dioptric power matrices. These matrices extend the concept to astigmatic lenses by considering different powers in different meridians, essentially applying the principles of the Lens Maker's Formula in multiple dimensions.

What is the relationship between the Lens Maker's Formula and the concept of equivalent power in a lens system?

The Lens Maker's Formula gives the power of a single lens. In a lens system, the equivalent power is often calculated by adding the powers of individual lenses (in the thin lens approximation). Understanding the Lens Maker's Formula is crucial for calculating these individual powers and thus the overall equivalent power of the system.

Can the Lens Maker's Formula be applied to non-spherical lenses, such as cylindrical or toric lenses?

The standard Lens Maker's Formula is specifically for spherical lenses. For non-spherical lenses like cylindrical or toric lenses, modified versions of the formula are used that take into account the different curvatures in different planes. These modifications are crucial in designing lenses for astigmatism correction.

How does the Lens Maker's Formula relate to the concept of cardinal points in a lens system?

While the Lens Maker's Formula doesn't directly give cardinal points (focal points, principal points, and nodal points), it's fundamental to understanding them. The formula provides the focal length, which is a key cardinal point. For thick lenses and systems, more complex calculations based on this formula help determine all cardinal points.

What is the significance of the Lens Maker's Formula in understanding the optics of the human eye?

The Lens Maker's Formula helps in understanding how the shape and refractive index of the eye's lens contribute to its focusing power. It's crucial in explaining how the eye focuses light and how vision problems like myopia and hyperopia relate to changes in the eye's effective focal length.

The Lens Maker’s Formula - Definition, Solved Examples, FAQs

Team Careers360Updated on 02 Jul 2025, 05:07 PM IST

In this article, we will discuss about, what is lens maker’s formula? What is radius of curvature of lens? What is lens maker formula for concave lens? What is lens maker equation? What is relation between focal length and refractive index? What is curvature of lens? So let’s see,

The Lens Maker’s Formula

What is lens maker’s formula?

Lens is a refracting object (device), which include of a transparent material. It can have 2 curved s/f (surfaces) or 1 curved and 1 plane s/f (surface). Basically, lenses can be categorized or classified as convex (converging) and concave lenses (diverging).

Definition: Real lenses have the limited thickness between their two exterior/surfaces of curvature. An ideal thin lens with two surfaces of uniform curvature will have zero refracting (optical) power. It means it wills neither convex nor concave light. A lens with some thickness which is not trivial is called a thick lens.

The focal length of a lens depends on the index of refraction (refractive index) of the lens and the radii of curvature. The lens maker’s equation is second formula used for lenses that provide us a relationship betwixt the focal distance (length), index of refraction, and radii of curvature of the two spheres used in lenses. It is employed by lens manufacturers to form the lenses of particular power from the glass of a given index of refraction.

Lenses are of two kinds based on the curvature of the two refracting surfaces. Convex and concave.

Also read -

What is lens maker’s Equation?

Lens maker’s Equation/formula for thin lens:

Lens maker formula is used to assemble a lens with the itemize focal length. A lens has 2 curved surfaces, but these are not exactly the selfsame. If we know the index of refraction and the radius of the curvature of both the surface, then we can find out the focal length of the lens by using the given lens maker’s formula:

1/f=(μ-1)×(1/R1 - 1/R2)

Where,

f=focal length of the lens

μ= Refractive index

R1 and R2 = Radius of the curvature of both 2 surface

It is signify that the lens should be thin so that the segregation betwixt the two refracting surfaces should be small. Also, the medium on either side of the lens should be the equal or same.

Also Read:

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Lens maker’s Equation/formula for thick lens:

Lenses where the thickness is minor, such that they are considered negligible in contrast to the radius of curvature, are mentioned to as thin lenses.

If the thickness of lens has to be considered in comparison to the radius of curvature, the below lens formula for thick lenses can be used.

1/f=(n-1)[1/R1 - 1/R2 + (n-1)d/(n×R1 R2) ]

Where,

d = thickness of the lens in consideration

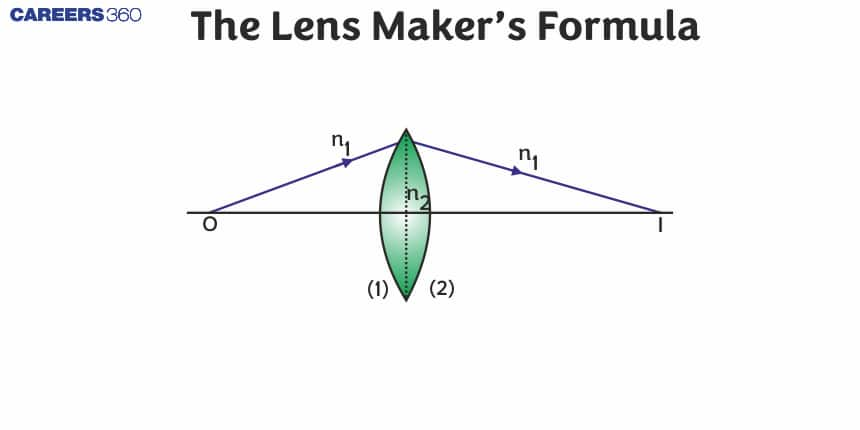
While, another concept that has to be contemplated is the lens maker’s formula accounting for objects that are present in divergent media. The equation is as given,

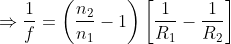1648554992043 Where,

n1 = refractive index of the lens in consideration

n2 = refractive index of the external medium

Related Topics Link,

What is lens maker formula for convex lens?

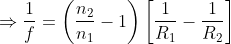
1648555203607

If the ambient medium is taken to be air i.e. n1≈1 and n2= n is taken into account, the optician formula are often given within the usual form.

Lens Maker Formula for Concave Lens and Convex Lens

For a concave lens, R1 is -ve and R2 is +ve. The lens maker formula for concave lens is represented as,

1/f=-(n2/n1-1)[1/R1 + 1/R2]

For a convex lens, R1 is +ve and R2 is -ve. The lens maker formula shown in the form,

1/f=(n2/n1-1)[1/R1 + 1/R2]

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

Q: How does the Lens Maker's Formula relate to the concept of aplanatic points in a lens?

Aplanatic points are positions where a lens produces no spherical aberration or coma. While the Lens Maker's Formula doesn't directly give these points, understanding how lens shape affects focusing

Q: Can the Lens Maker's Formula be used to understand the principle of adaptive optics?

While adaptive optics systems are complex, the Lens Maker's Formula provides a foundation for understanding them. It shows how changing the curvature of a lens surface affects focal length, which is the basic principle behind deformable mirrors and other adaptive elements used to correct wavefront aberrations.

Q: How does the Lens Maker's Formula help in explaining the concept of lens neutralization in optometry?

Lens neutralization involves finding the power of an unknown lens. The Lens Maker's Formula helps explain why certain neutralizing techniques work. For instance, when a lens is placed on a flat surface, the observed power relates to the formula's prediction based on the lens's back surface curvature.

Q: What role does the Lens Maker's Formula play in understanding the optics of contact lenses?

The Lens Maker's Formula is crucial in contact lens design. It helps in calculating the required curvatures and thickness of the lens to achieve the desired corrective power, taking into account the refractive index of the lens material and the optics of the eye it will be placed on.

Q: How does the Lens Maker's Formula relate to the concept of lens power in different meridians for astigmatism correction?

For astigmatism correction, lenses have different powers in different meridians. While the standard Lens Maker's Formula doesn't directly apply, it forms the basis for understanding how different curvatures in different meridians result in different focusing powers, which is crucial for astigmatism correction.

Q: Can the Lens Maker's Formula be used to explain how bifocal or multifocal lenses work?

The Lens Maker's Formula helps explain bifocal and multifocal lenses by showing how different curvatures result in different focal lengths. While these lenses are more complex, understanding how shape affects focal length is key to grasping how different parts of the lens provide different focusing powers.

Q: How does the Lens Maker's Formula contribute to the design of zoom lenses?

While zoom lenses involve complex systems, the Lens Maker's Formula is fundamental in designing each element. Understanding how changing radii and refractive indices affect focal length is crucial for creating lens elements that can be moved relative to each other to change the overall focal length of the system.

Q: How does the Lens Maker's Formula help in understanding the effect of lens shape on aberrations?

While the Lens Maker's Formula doesn't directly address aberrations, it shows how lens shape (through R1 and R2) affects focal length. This relationship is key to understanding how different lens shapes can be used to minimize various aberrations, even though more complex calculations are needed for detailed aberration analysis.

Q: How does the Lens Maker's Formula relate to the concept of back vertex power in optometry?

The back vertex power is the reciprocal of the back vertex focal length, which is measured from the back surface of the lens. While the Lens Maker's Formula gives the power based on the principal planes of the lens, understanding it helps in calculating and adjusting for back vertex power in thick lenses or lens systems.

Q: What role does the Lens Maker's Formula play in understanding spherical aberration?

While the Lens Maker's Formula doesn't directly account for spherical aberration, it helps in understanding its origin. The formula assumes all rays focus at the same point, but in reality, rays further from the optical axis focus at different points. This deviation from the ideal focal point predicted by the formula is spherical aberration.

Articles

Tamil Nadu BSc Nursing Admission 2025: Counselling (Started), Seat Matrix, Merit List

Sep 12, 2025

DU LLB Fee Structure 2026 - Check Complete Details

Sep 11, 2025

Top 5 Career Options after B.Arch - Eligibility, Salary Trends

Sep 11, 2025

Top 6 Career Options after BAF - Eligibility, Salary

Sep 06, 2025