Mirror Formula for Spherical Mirrors

Mirror Formula for Spherical Mirrors - Detailed Guide

Edited By Team Careers360 | Updated on Jul 02, 2025 05:04 PM IST

In this article we are going to learn about the formula for spherical mirror ,sign convention for concave mirror, sign convention for convex mirror and also the sign convention for spherical lenses.
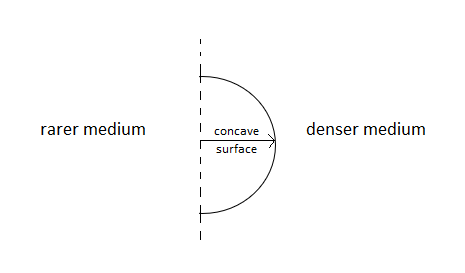
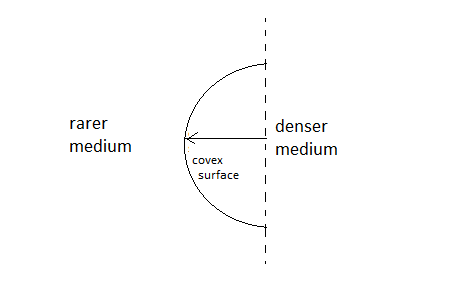
A spherical refracting surface is the part of a sphere separating two transparent media .There are two types of spherical refracting surfaces.

Mirror Formula for Spherical Mirrors - Detailed Guide

Concave spherical refracting surface

$Concave spherical refracting surface$

Convex spherical refracting surface

$Convex spherical refracting surface$

The spherical refracting surfaces have such components:

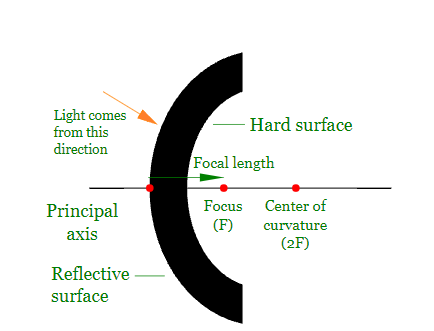
$spherical refracting surfaces$

Pole : The midpoint of a spherical refracting surface is called pole of the spherical surface.
Centre of curvature : The centre of the sphere which forms a curved refracting surface , is known as centre of curvature.
Radius of curvature : The radius of the sphere of which the refracting surface is a part is called the radius of curvature.
Principal axis : The straight line joining the pole and the centre of curvature of the spherical refracting surface and the extended on both sides is called the principal axis of the surface.
Aperture: The effective diameter of the refracting spherical surface exposed to the incident light is called the aperture.

Also read -

What is sign convention?

It is a selection of physical significance of signs for a particular quantity.

For sign convention we need to follow some assumptions/write the rules for sign convention:

The refraction through the spherical surface follows the following assumptions

The object has to be a point object and it will lie on the principal axis.
The aperture has to be small on the spherical refracting surface.
Refraction of paraxial rays will be considered only.

Related Topics Link,

Sign convention for mirror/sign convention for spherical mirror/ sign convention for reflection by spherical mirror:

If the principal axis of the spherical reflecting surface is x-axis and distances along the y-axis above the principal axis, then the principal axis is taken as a positive sign and the y axis below the x-axis is taken as a negative sign.
All distances are measured from the pole of the spherical surface.
The distance measured from the pole in the direction opposite to the direction of the incident ray is taken as a negative sign and the measured direction of the incident ray is taken as a positive sign.
The sign convention for a convex lens and concave mirror is the same.
The sign convention for a concave lens and a convex mirror is the same.

Relation between focal length (f) and radius of curvature (r) :

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

r=2f

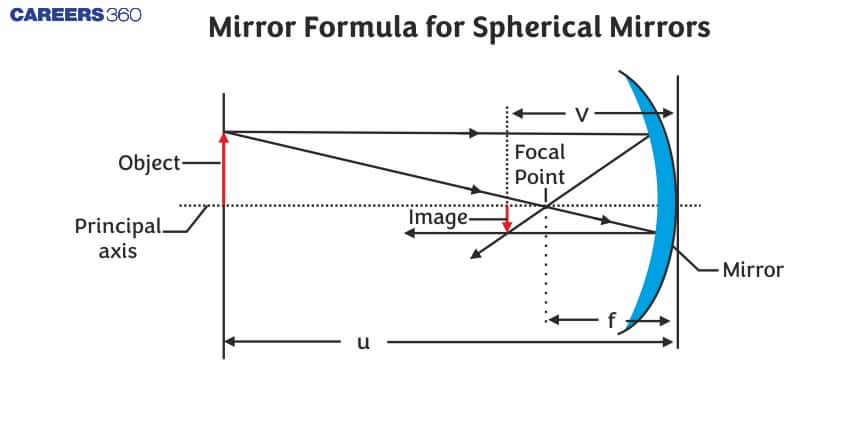
The general equation for lens / spherical mirror formula:

1/v+1/u=1/f

Where v is the image distance, u is the object distance f is the focal length of the lens.

This is also the formula for conjugate foci.

Linear magnification formula :

m=-v/u

m is the linear magnification of the lens.

Linear magnification can also be the ratio of the height of the image to the height of the object.

m=I/O

=length or height of the image / length or height of the object

Longitudinal or axial magnification:

m_A=length of the image along the principal axis / length of the object along the principal axis

The spherical mirror longitudinal magnification is equal to the square of the linear magnification.

m_A=m²

The general form of refraction of light at the common spherical surface is when the light rays move from medium 1 to medium 2.

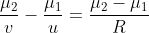
$\frac{\mu_2}{v}-\frac{\mu_1}{u}=\frac{\mu_2-\mu_1}{R}$

µ₁= refractive index of medium 1

µ₂ = refractive index of medium 2

R = radius of curvature of a spherical surface.

Also Read:

xy=f²

Where, x = u – f ; y = v – f

Lens maker’s formula :

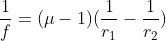
$\frac{1}{f}=(\mu-1)(\frac{1}{r_1}-\frac{1}{r_2})$

Where = refractive index of the material of the lens with respect to the surrounding medium.

r₁= radius of curvature of the medium 1 ;

r₂ = radius of curvature of the medium 2.

Power of a lens:

Power can be expressed as:

P=1/f

Here, f is focal length (meters) and D is the unit of power which is measured in dioptre.

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. What is the sign of focal length?

Focal length of a concave mirror is taken as the negative and the focal length of a convex mirror is taken as positive.

2. What are conjugate foci?

The pair of points is such that when an object is placed at one focal point on one side the image will be formed at the other focal point on the other side . These two focal points are called conjugate foci.

3. What is an optical centre?

The point on the principal axis of the lens through which the rays of light emerge out without deviation after refraction is known as the optical centre of the lens.

4. What is a thin lens?

If the thickness of a lens is much less than the radius of curvature of two surfaces then that lens is known as a thin lens.

5. What is the focal length of a lens?

Focal length is the distance between the optical centre and the principal focus of a lens.

6. How does the mirror formula differ for concave and convex mirrors?

The mirror formula (1/f = 1/v + 1/u) remains the same for both concave and convex mirrors. However, the sign conventions for u, v, and f differ. For concave mirrors, f is positive, while for convex mirrors, f is negative.

7. What are the sign conventions used in the mirror formula?

The sign conventions are: (1) All distances are measured from the pole of the mirror. (2) Distances measured in the direction of incident light are positive. (3) Distances measured against the direction of incident light are negative. (4) Heights above the principal axis are positive, and below are negative.

8. Why is the focal length of a convex mirror always negative?

The focal length of a convex mirror is always negative because its focus is located behind the mirror surface, in the virtual space. This is consistent with the sign convention where distances measured opposite to the direction of incident light are considered negative.

9. Can the mirror formula be used to predict whether an image will be real or virtual?

Yes, the mirror formula can help predict if an image is real or virtual. If the calculated value of v is positive, the image is real and on the same side as the reflected rays. If v is negative, the image is virtual and behind the mirror.

10. How does the mirror formula apply to plane mirrors?

For plane mirrors, the focal length (f) is infinite. Applying this to the mirror formula (1/f = 1/v + 1/u) gives 1/∞ = 1/v + 1/u, which simplifies to v = -u. This means the image distance is equal to the object distance but on the opposite side of the mirror.

11. What is the mirror formula for spherical mirrors?

The mirror formula for spherical mirrors is 1/f = 1/v + 1/u, where f is the focal length, v is the image distance, and u is the object distance. This formula relates the position of the object, image, and focal point of a spherical mirror.

12. How does the mirror formula relate to the magnification of an image?

The mirror formula is related to magnification through the equation m = -v/u, where m is magnification, v is image distance, and u is object distance. This shows how the relative positions of object and image affect the size of the image formed.

13. How does changing the object distance affect the image formation in a spherical mirror?

As the object distance (u) changes, the image distance (v) changes according to the mirror formula. Generally, as u increases, v decreases for a given focal length. This affects the size, position, and nature (real/virtual) of the image formed.

14. What happens to the image when an object is placed at the center of curvature of a concave mirror?

When an object is placed at the center of curvature of a concave mirror, its image is formed at the same point. The image is real, inverted, and the same size as the object. This is because the center of curvature is twice the focal length (C = 2f).

15. Why is the focal length half the radius of curvature for spherical mirrors?

The focal length is half the radius of curvature because of the geometry of spherical mirrors. Light rays parallel to the principal axis converge at a point halfway between the center of curvature and the mirror's surface, which defines the focal point.

16. How does the mirror formula relate to the concept of optical power?

The optical power (P) of a mirror is the reciprocal of its focal length: P = 1/f. The mirror formula (1/f = 1/v + 1/u) can be rewritten as P = 1/v + 1/u, directly relating the optical power to object and image distances.

17. Can the mirror formula be used for non-spherical mirrors?

The mirror formula as stated (1/f = 1/v + 1/u) is specifically for spherical mirrors. For non-spherical mirrors, such as parabolic mirrors, modifications or different formulas are needed to accurately describe image formation.

18. How does the mirror formula help in understanding the concept of infinite focal length?

When a mirror has an infinite focal length (like a plane mirror), 1/f becomes zero in the mirror formula. This leads to 1/v = -1/u, explaining why plane mirrors form virtual images at the same distance behind the mirror as the object is in front.

19. What role does the mirror formula play in correcting spherical aberration?

While the mirror formula itself doesn't correct spherical aberration, understanding it helps in designing mirrors that minimize this effect. By manipulating the relationship between focal length and mirror curvature, optical engineers can reduce spherical aberration in advanced mirror designs.

20. How does the mirror formula apply to concave mirrors used in telescopes?

In telescopes, concave mirrors are often used as the primary mirror. The mirror formula helps in determining the optimal placement of the secondary mirror or eyepiece relative to the primary mirror's focal point, ensuring proper image formation and magnification.

21. How does the mirror formula relate to the concept of lateral magnification?

The mirror formula is closely related to lateral magnification (m) through the equation m = -v/u. This relationship shows how the relative distances of the object and image from the mirror affect the size of the image compared to the object.

22. What happens when an object is placed at the focal point of a concave mirror according to the mirror formula?

When an object is at the focal point, u = f. Substituting this into the mirror formula (1/f = 1/v + 1/f) results in 1/v = 0, or v = ∞. This means the image is formed at infinity, representing parallel rays reflected from the mirror.

23. Can the mirror formula be derived from the laws of reflection?

Yes, the mirror formula can be derived from the laws of reflection and the geometry of spherical mirrors. It's a mathematical representation of how incident rays reflect off the curved surface to form an image, based on the principle that the angle of incidence equals the angle of reflection.

24. How does the mirror formula account for the curvature of spherical mirrors?

The mirror formula implicitly accounts for curvature through the focal length (f). The focal length is directly related to the radius of curvature (R) by the equation f = R/2 for spherical mirrors. This relationship embeds the mirror's curvature into the formula.

25. How does the mirror formula help in understanding the concept of infinite object distance?

When an object is at infinity, 1/u approaches zero in the mirror formula. This simplifies the equation to 1/f = 1/v, meaning the image is formed at the focal point. This concept is crucial in understanding how mirrors focus parallel light rays from distant objects.

26. What role does the mirror formula play in understanding the concept of magnification at different object positions?

The mirror formula, combined with the magnification equation (m = -v/u), shows how magnification changes with object position. As u changes, v changes accordingly, affecting the magnification. This relationship helps predict image size for different object placements.

27. How can the mirror formula be used to find the position where an object creates an image of the same size?

To find where an object creates an image of the same size, we need m = 1 or -1. Using m = -v/u and the mirror formula, we can solve for u. For a magnification of 1 (upright image), the object must be at the center of curvature (u = 2f) for a concave mirror.

28. What does the mirror formula tell us about the relationship between object distance and image distance?

The mirror formula shows an inverse relationship between object distance (u) and image distance (v). As one increases, the other generally decreases for a given focal length, demonstrating how changing object position affects image formation.

29. How does the mirror formula relate to the concept of depth of field in curved mirrors?

While the mirror formula doesn't directly address depth of field, it can be used to understand how small changes in object distance affect image position. This relationship is crucial in determining the range of distances over which objects appear in acceptable focus.

30. How can the mirror formula be used to design a spherical mirror with specific imaging properties?

By manipulating the mirror formula, designers can determine the required focal length (and thus the radius of curvature) for a mirror to produce images with desired characteristics (e.g., specific magnification or image position) for given object distances.

31. What does the mirror formula tell us about the limit of real image formation in concave mirrors?

The mirror formula shows that for concave mirrors, real images (positive v) are only formed when the object is beyond the focal point. When the object is at or within the focal point, the formula yields negative or undefined v, indicating virtual image formation.

32. How does the mirror formula help in understanding the concept of infinite magnification?

Infinite magnification occurs when v approaches infinity in the magnification formula (m = -v/u). The mirror formula shows this happens when the object is placed at the focal point (u = f), as this makes 1/v = 0, or v = infinity.

33. How does the mirror formula relate to the concept of focal plane in spherical mirrors?

The focal plane is perpendicular to the principal axis at the focal point. The mirror formula helps locate this plane by determining the focal length (f). Understanding the focal plane is crucial for predicting image formation for off-axis objects.

34. What role does the mirror formula play in understanding the concept of caustics in spherical mirrors?

While the mirror formula assumes perfect image formation, it can be used as a starting point to understand caustics. Deviations from the ideal image point predicted by the formula, especially for rays far from the axis, contribute to the formation of caustics in spherical mirrors.

35. How can the mirror formula be used to explain the difference in image formation between concave and convex mirrors?

The mirror formula, with appropriate sign conventions, shows that concave mirrors (positive f) can produce both real and virtual images depending on object position, while convex mirrors (negative f) always produce virtual images, explaining their fundamental difference in image formation.

36. What does the mirror formula reveal about the relationship between a mirror's focal length and its imaging capabilities?

The mirror formula shows that the focal length (f) is a key determinant of a mirror's imaging behavior. Mirrors with shorter focal lengths produce more dramatic changes in image position and size as object distance varies, while longer focal lengths result in more gradual changes.

37. How does the mirror formula help in understanding the concept of conjugate points in mirror optics?

Conjugate points are pairs of points where one is the object and the other its image. The mirror formula relates these points mathematically, showing how changing one point's position affects the other, maintaining the relationship 1/f = 1/v + 1/u.

38. Can the mirror formula be used to predict the position where a real image transitions to a virtual image in a concave mirror?

Yes, the transition point is at the focal point of the concave mirror. The mirror formula shows that when u = f, v becomes infinite, and for any u < f, v becomes negative, indicating the transition from real to virtual image formation.

39. What does the mirror formula tell us about the relationship between a mirror's radius of curvature and its focal length?

The mirror formula doesn't directly include the radius of curvature, but it's related to focal length by R = 2f for spherical mirrors. This relationship is implicit in the formula and is crucial for understanding how a mirror's shape affects its imaging properties.

40. What role does the mirror formula play in understanding the concept of spherical aberration?

While the mirror formula assumes perfect image formation, deviations from it for rays far from the axis help explain spherical aberration. The formula provides the ideal image point, and discrepancies from this point for different rays contribute to understanding aberration effects.

41. How does the mirror formula help in explaining the use of concave mirrors in solar concentrators?

The mirror formula shows how parallel rays (effectively from an object at infinity) converge at the focal point of a concave mirror. This principle is key to solar concentrators, where sunlight (parallel rays) is focused to a point for energy concentration.

42. Can the mirror formula be used to explain why images in convex mirrors appear closer than they are?

Yes, the mirror formula for convex mirrors always yields a negative v (image distance) that is smaller in magnitude than u (object distance). This mathematical relationship explains why images in convex mirrors appear closer and smaller than the actual objects.

43. How does the mirror formula help in determining the nature of the image?

The mirror formula helps determine the nature of the image by giving the image distance (v). If v is positive, the image is real; if negative, it's virtual. Combined with the magnification formula, it also indicates whether the image is upright or inverted.

44. What is the significance of the 'New Cartesian Sign Convention' in the mirror formula?

The New Cartesian Sign Convention provides a consistent system for assigning signs to distances in the mirror formula. It helps in correctly applying the formula and interpreting its results, ensuring that the calculations accurately represent the physical reality of image formation.

45. Can the mirror formula predict when no image will be formed?

Yes, the mirror formula can predict when no real image is formed. For instance, if the calculated value of v is negative for a concave mirror, it indicates that no real image is formed; instead, a virtual image is created behind the mirror.

46. How does the mirror formula help in understanding the concept of virtual focus in convex mirrors?

For convex mirrors, the mirror formula uses a negative focal length, representing the virtual focus behind the mirror. This negative f in the equation (1/f = 1/v + 1/u) helps explain why convex mirrors always form virtual, upright images regardless of object position.

47. What is the relationship between the mirror formula and the thin lens formula?

The mirror formula (1/f = 1/v + 1/u) is mathematically identical to the thin lens formula. The main difference is in the sign conventions used and the physical interpretation of the terms, as mirrors reflect light while lenses refract it.

48. Can the mirror formula be used to explain why convex mirrors always produce virtual images?

Yes, the mirror formula explains this. For convex mirrors, f is negative. No matter what positive value of u is used, v will always be negative (indicating a virtual image) when solved in the equation 1/f = 1/v + 1/u, where f is negative.

49. How does the mirror formula relate to the concept of real and virtual images?

The mirror formula helps distinguish between real and virtual images through the sign of v (image distance). A positive v indicates a real image formed in front of the mirror, while a negative v represents a virtual image behind the mirror.

50. How does the mirror formula help in understanding the concept of virtual objects?

While less common, virtual objects can be considered in the mirror formula by using a negative value for u. This situation might arise when dealing with multiple mirror systems or when analyzing the image from one mirror as the object for another.

51. Can the mirror formula be used to explain why concave mirrors can form both real and virtual images?

Yes, the mirror formula explains this versatility of concave mirrors. Depending on the object's position relative to the focal point, the calculated v can be either positive (real image) or negative (virtual image), showing how concave mirrors can produce both types of images.

52. What does the mirror formula reveal about the image formation when an object is placed between the focal point and a concave mirror's surface?

When an object is between the focal point and a concave mirror's surface, the mirror formula yields a negative v, indicating a virtual, upright, and enlarged image behind the mirror. This explains the magnifying effect of concave mirrors in this configuration.

53. Can the mirror formula be used to explain why convex mirrors always produce diminished images?

Yes, the mirror formula, combined with the magnification equation, explains this. For convex mirrors, v is always negative and smaller in magnitude than u. This results in a magnification (m = -v/u) that is always positive but less than 1, indicating a diminished image.

54. How does the mirror formula relate to the concept of optical axis in spherical mirrors?

The mirror formula assumes measurements along the optical (principal) axis. It helps in understanding how object and image positions relate to this axis, which is crucial for predicting image characteristics and understanding the symmetry of the optical system.

55. How can the mirror formula be used to understand the concept of virtual focus in convex mirrors?

For convex mirrors, the mirror formula uses a negative focal length, representing the virtual focus behind the mirror. This explains why convex mirrors always form virtual images and helps in calculating the position of these virtual images.