Into Function and Bijective Function: Definition & Differences

Functions can be defined as the relation between two sets where every element in one set has a unique element in another. A bijective functions are one of an important topic in set theory and Mathematics. These concepts are used in various fields like calculus, physics, engineering etc.

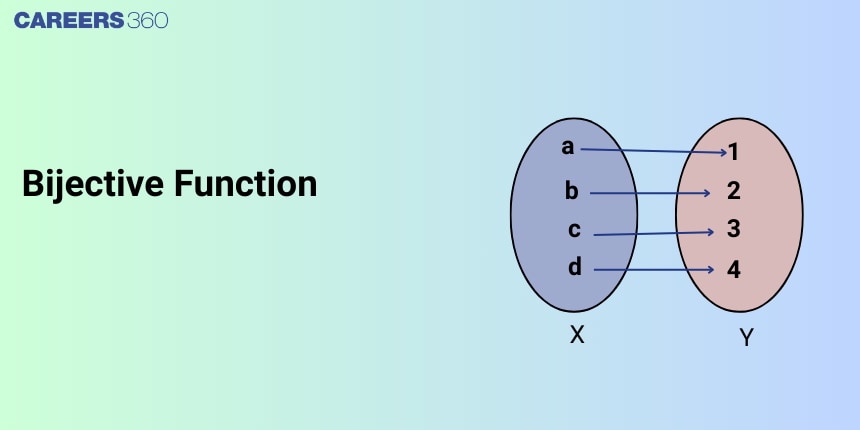
In this article, we will cover the concepts of bijective function. This concept falls under the broader category of sets relation and function, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of seven questions have been asked on this concept, including one in 2019, one in 2021, one in 2022, and four in 2023.

Function

$A$ and $B$ are two non-empty sets, then a relation from $A$ to $B$ is said to be a function if each element $x$ in $A$ is assigned a unique element $f(x)$ in $B$, and it is written as

$f: A ➝ B$ and read as $f$ is mapping from $ A$ to $B.$

Domain of a function

All possible values of $x$ for $f(x)$ is defined $(f(x)$ is a real number) is known as a domain.
If a function is defined from $A$ to $B$ i.e. f: $A \rightarrow B$, then all the elements of $\operatorname{set} A$ is called the Domain of the function.

Co-domain of a function

If a function is defined from $A$ to $B$ i.e. $f: A \rightarrow B$, then set $B$ is called the Co-domain of the function.

Range of a function

It is defined as all the values that the function assumes or in other words we can also say the output of the given function. It is also known as the image set of the function.

Injective function(one-one function)

A function $f: A \rightarrow B$ is called one - one function if distinct elements of $A$ have distinct images in $B$.

Eg. $f: X \longrightarrow Y$, function given by $y=f(x)=x$, and
$X=\{-2,2,4,6\}$ and $Y=\{-2,2,4,6\}$

Surjective Function(onto function)

A function $f: A \rightarrow B$ is said to be onto function if the range of $f$ is equal to the co-domain of $f$.

Eg.

$\mathrm{X}=\left\{\mathrm{x}_1, \mathrm{x}_2, \mathrm{x}_3, \mathrm{x}_4\right\}$ and $\mathrm{Y}=\left\{\mathrm{y}_1, \mathrm{y}_2, \mathrm{y}_3\right\}$

$
f: X \rightarrow Y
$

Bijective Function

A function $f: X \rightarrow Y$ is said to be bijective, if $f$ is both one-one and onto (both injective and surjective)

Eg.
Consider, $\mathrm{X}_1=\{1,2,3\}$ and $\mathrm{X}_2=\{\mathrm{x}, \mathrm{y}, \mathrm{z}\}$

$
f: X_1 \rightarrow X_2
$

The function f is a injective function as the every distinct elements in $X_1$ has unique images in $X_2$ and a surjective function as every elemt in $X_2$ has a pre-image in $X_1$.

The number of bijective functions

If $\mathrm{f}(\mathrm{x})$ is bijective, and the function is from a finite set A to a finite set B , then $n(A)=n(B)=m($ Say $)$ And, the number of Bijective functions $=\mathrm{m}$ !

While mapping the two functions, i.e., the mapping between $A$ and $B$ (where $B$ need not be different from $A$) to be a bijection,

• each element of $A$ must be paired with at least one element of $B$,
• no element of $A$ may be paired with more than one element of $B$,
• each element of B must be paired with at least one element of $A$, and
• no element of B may be paired with more than one element of $A$.

Difference between Injective, Surjective, and Bijective Function

S.No	Injective Function	Surjective Function	Bijective Function
1	A function that always maps the distinct element of its domain to the distinct element of its codomain	A function that maps one or more elements of $A$ to the same element of $B$	A function that is both injective and surjective
2	It is also known as one-to-one function	It is also known as onto function	It is also known as one-to-one correspondence
3

Some examples of Bijective functions are:

• Linear functions: $f(x) = x, g(x) = x + 10, h(x) = 5x – 5$, etc.
• Polynomial Functions: $f(x) = x^3, g(x) = x^3 – 1 $
• Exponential functions: $f(x) = e^x, where f : R → (0, \infty)$
• Absolute Value Function: $f(x) = x|x|$

Properties

• Inverse Exists: A bijective function has an inverse function that undoes the mapping, taking an element from the codomain back to an element in the domain.
• Unique Inverse: The inverse of a bijective function is unique, meaning there is only one function that reverses the mapping.
• Preservation of Composition: If you compose a bijective function with another function, the composition is also bijective.

How to Identify a Bijective Functions?

To figure out if a function is bijective, there is a 2 step process to identify:

1. Injective function
2. Surjective function

If the give function is both injective and surjective, then it is a bijective function.

Recommended Video Based on Into and Bijective Functions

Solved Examples Based On the Into and Bijective Functions

Example 1: Let $f: N \rightarrow Y$ be a function defined as $f(x)=4 x+3$ where $Y=\{y \in N: y=4 x+3$ for some $x \in y\}$. Show that $f$ is invertible and its inverse is?

Solution:
As we learned in
Bijective Function -
The function that is both one-on-one and onto is the Bijective Function.

$
f(x)=4 x+3
$

Let $y=4 x+3$

$
\frac{y-3}{4}=x=g(y)
$

Example 2: If $n(A)=3$ and $n(B)=5$. How many bijective functions are possible from $A$ to $B$ ?
Solution:

If $n(A)=n(B)=m$, then the number of bijective functions from $A$ to $B=m!$.
Here, $n(A) \neq n(B)$
So, bijective functions are not possible.
Hence, the answer is 0 .

Example 3: Which of the following function is a bijective function?

1) $f(x)=\frac{x^2-4}{x-2}$

2) $f(x)=x^2$

3) $f_3(x)=3 x+4$

4) $f_4(x)=\frac{x^2-1}{x+1}$

Solution:

$f_1(x)$ is not defined for $\mathrm{x}=2$, and it does not have 4 in its range, so into and thus not bijective $f_4(x)$ is not defined for $\mathrm{x}=-1$, and does not have -2 in its range, so not bijective $f_3(x)=3 \mathrm{x}+4$ is defined for $\mathrm{x} \in \mathrm{R}$ and it is a one-one and onto function: bijective function $f_2(x)$ is not a one - one function

Hence, the answer is the option 3.

Example 4: If $n(A)=4$ and $n(B)=4$. Then how many bijective functions can be formed from $A$ to $B$ ?
1) $24$
2) $6$
3) $120$
4) $0$

Solution:

As we have learned
Number of Bijective Function
If $\mathrm{f}(\mathrm{x})$ is a bijection, then $n(A)=n(B)=m($ Say $)$
And the number of Bijective functions $=m$ !
Here, number of bijective function $=4!=24$
Hence, the answer is the option 1.

Example 5: If set $A$ has $5$ elements and set $B$ has $3$ elements. How many bijective function can be formed from $A$ to $B$ ?

1) $120x$
2) $6$
3) $0$
4) $24$

Solution:

As we have learned

Number of Bijective Function
If $\mathrm{f}(\mathrm{x})$ is bijective then $n(A)=n(B)=m($ Say $)$
And the number of Bijective functions $=m$ !

Here

There can be no bijective function from $A$ to $B$ since number of elements should be same for both the sets to form a bijective function

Hence, the answer is the option 3.