Functions Transformations - Graphing, Rules, Tricks

Transformations of Functions

Transformation of functions moves or changes the size, position and the shape the graph of the function. The transformation of the functions can be classified into Dilation transformation, Rotation transformation, Reflection transformation and Translation transformtion.

Dilation Transformation

Dilation transformaton is when the function is transformed such that the graph of the function is either stretched or shrinked.

$f(x) → af(x) , a>1$

Stretching of a graph along the y-axis occurs if we multiply all outputs y of a function by the same positive constant (here '$a$' ).

$\mathrm{f}(\mathrm{x}) \rightarrow \frac{1}{\mathrm{a}} \mathrm{f}(\mathrm{x})$ $(a > 1)$

Shrinking of a graph along the y-axis occurs if we multiply all outputs y of a function by the same positive constant (here '$\frac{1}{a}$' ).

For Example :

The graph of the function $f(x)=3 x^2$ is the graph of $y=x^2$ stretched vertically by a factor of $3$ , whereas the graph of $f(x)=\frac{1}{3} x^2$ is the graph of $y=x^2$ compressed vertically by a factor of $3$ .

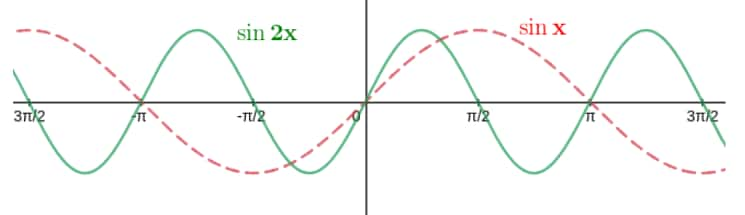
$f(x)$ transforms to $f(ax), (a>1)$

Shrink the graph of $f(x)$ ‘$a$' times along the $x$-axis after drawing the graph of $f(x)$,

$f(x)$ transforms to $f(x/a), (a>1)$

Stretch the graph of $f(x)$ ‘$a$’ times along the $x$-axis after drawing the graph of $f(x)$,

For Example: The graph of $f(x)=\sin x, f(x)=\sin (2 x)$, and $f(x)=\sin (x / 2)$.

Rotation Transformation

Rotation transformaton is when the function is transformed such that the graph of the function is rotated $90^o, 180^o$ or $270^o$.

To rotate a graph, change the coordinates $(x,y)$,

$90^o$$: (x,y) \rightarrow (-y,x)$

$180^o$$: (x,y) \rightarrow (-x,-y)$

$270^o$$: (x,y) \rightarrow (y,-x)$

Reflection Transformation

Reflection transformation is when the function is transformed such that the graph of the function is fliped to the opposite side without any change in the shape of size.

Transformation $f(x) → f(-x),$

When we multiply all inputs by $−1$, we get a reflection about the y-axis

So, to draw $y = f(-x)$, take the image of the curve $y=f(x)$ in the $y$-axis as a plane mirror

For example,

The graph of $y=e^x,$ $y= e^(-x) $

$f(x) → -f(x) :$

When multiplying all the outputs by $−1$, we get a reflection about the $x$-axis.

To draw $y = -f(x)$ take an image of $f(x)$ in the x-axis as a plane mirror

For example

The graph of $y=e^x,$ $y=-e^x $ (Transformation $f(x) \rightarrow-f(x)$ )

Translation Transformation

Translation transformaton is when the function is transformed such that the graph of the function is shifted.

To translate a graph,

- Horizontally to the left, $f(x) → f(x+a)$

- Horizontally to the right, $f(x) → f(x-a)$

- Vertically upwards, $f(x) → f(x)+a$

- Vertically downwards,$f(x) → f(x)-a$

Other Transformations

$f(x) →|f(x)|$

When $y = f(x)$ given

1. Leave the positive part of $f(x)$ (the part above the $x$-axis) as it is

2. Now, take the image of the negative part of $f(x)$ (the part below the x-axis) about the $x$-axis.

OR

Take the mirror image in the x-axis of the portion of the graph of $f(x)$ which lies below the $x$-axis

For Example:

$y=x^3$ $y=|x³|$ $y=|x³|$ and $y=x^3$

Transformation $f(x) →f(|x|) $

When $y = f(x)$ given

1. Leave the graph lying right side of the $y$-axis as it is

2. The part of $f(x)$ lying on the left side of the $y$-axis is deleted.

3. Now, on the left of the $y$-axis take the mirror image of the portion of $f(x)$ that lying on the right side of the $y$-axis.

For Example:

$y = f(x)$ $ y = f(x) and y = f(|x|) $ $y = f(|x|) $

Transformation $f(x) → |f(|x|)|$

1. First $f(x)$ is transforms to $|f(x)|$

2. Then $|f(x)|$ transforms to $|f(|x|)|$

Or

(i) $f(x) \rightarrow|f(x)|$
(ii) $f(x) \rightarrow f(|x|)$

For Example:

$y = f(x)$ $ y = |f(x)| $

$y = f(|x|)$

$ y = |f(|x|)|$

$y=f(x) → |y| = f(x)$

$y = f(x)$ is given

1. Remove the part of the graph which lies below x-axis

2. Plot the remaining part

3. take the mirror image of the portion that lies above the x-axis about the x-axis.

Recommended Video Based on Transformation of Functions

Solved Examples Based on Transformation of Functions:

Example 1: The area bounded by the lines $y=|| x-1|-2|$ and $y=2$ is

1) $8$

2) $10$

3) $12$

4) $6$

Solution

Given the equation of curve are

$y = ||x-1|-2|$

and, $y = 2$

Plot the curve on the graph

$\begin{aligned}
& \text { Area }=\frac{1}{2} \times 2 \times C D+\frac{1}{2} \times 2 \times D E \\
& \text { Area }=C D+D E=8
\end{aligned}$

Example 2: The number of elements in the set $\{x \in \mathbb{R}:(|x|-3)|x+4|=6\}$ is equal to :

1) $3$

2) $4$

3) $1$

4) $2$

Solution

$\begin{aligned} & x \neq-4 \\ & (|x|-3)(|x+4|)=6 \\ & \Rightarrow \quad|x|-3=\frac{6}{|x+4|}\end{aligned}$

No. of solutions = $2$

Example 3: Which of the following is the graph of $|y| = cos x$?

1)

2)

3)

4)

Solution

As we have learnt in

$
y=f(x) \rightarrow|y|=f(x)
$

$y=f(x)$ is given
1. Remove the part of the graph which lies below ${x}$-axis
2. Plot the remaining part
3. take the mirror image of the portion that lies above $x$-axis about the $x$-axis.

First draw $y=\cos x$

Then,

1. Remove the part of the graph which lies below $x$-axis

2. Plot the remaining part

3. take the mirror image of the portion that lies above x-axis about the x-axis

Example 4: The number of solutions of $|\cos x|=\sin x$, such that $-4 \pi \leq x \leq 4 \pi$ is :

1) $4$
2) $6$
3) $8$
4) $12$

Solution

$2$ solutions in $(0,2 \pi)$
So $8$ Solutions in $[-4 \pi, 4 \pi]$

Hence correct option is 3