Relations and Functions
In our daily life, we often come across questions like “How is he related to you?” where answers such as “He is my brother” or “She is my mother” describe how two people are connected. This idea of connecting one object with another is what forms the basis of relations. In mathematics, relations and functions help us understand how different quantities or elements are linked together. In this article, you will find relations and functions class 12 notes, examples, formulas, and solutions explained in a simple and friendly way to strengthen your understanding and help you prepare for exams.
This Story also Contains
- What are Relations and Functions?
- Relation: Definition
- Function: Definition
- Representation of Relation and Function
- Difference Between Relations and Functions
- Types of Relations and Functions
- Types of Functions
- Relations and Functions: Formulae and Operations
- Recommended Books for Relations and Functions
- Practice Questions Based on Relations and Functions
What are Relations and Functions?
A relation in mathematics connects elements of two sets. It helps in identifying common terms between sets or functions. The total number of relations between two sets $A$ and $B$ depends on their sizes. Relations are fundamental to the study of functions, and they are widely used in areas like database systems, graph theory, and social networks.
Relation: Definition
A relation is a way to associate elements of one set with elements of another set. If two sets have values, a relation connects elements of the first set with those of the second.
A relation $R$ from a non-empty set $A$ to a non-empty set $B$ is a subset of the Cartesian product $A \times B$.
The subset is formed by specifying how the first element relates to the second in ordered pairs.
If $(a,b)$ belongs to $R$, where $a \in A$ and $b \in B$, it is written as $a R b$.
Example:
Let $A = \{1, 2\}$ and $B = \{x, y\}$. A relation can be: $R = \{(1, x), (2, y)\}$.
This means $1$ is related to $x$ and $2$ is related to $y$.
Domain of a Relation
The domain of a relation is the set of all first elements in the ordered pairs of the relation. It represents all possible inputs that have at least one output.
For example, if $R = \{(1, c), (5, a), (8, b)\}$, then the domain is: $\{1, 5, 8\}$.
Range of a Relation
The range of a relation is the set of all output values or second elements in the ordered pairs.
For the relation $R = \{(1, c), (5, a), (8, b)\}$, the range is: $\{c, a, b\}$.

Function: Definition
A function is a special kind of relation where each element in set $A$ is related to exactly one element in set $B$.
Formally, if $A$ and $B$ are two non-empty sets, a function $f: A \rightarrow B$ assigns each element $x \in A$ a unique element $f(x) \in B$.
This is written as: $f: A \rightarrow B$ (read as “$f$ is mapping from $A$ to $B$”).
Every function is a relation, but not every relation is a function.



First and second images represent a function as all the elements in set $A$ is mapped a element in set $B$ while the element $d$ in set $A$ is not mapped to any element in set $B$.

A function can be said as a subset of relation.
Image of a Function
The image of a function is the set of all output values produced from its domain.
Given a function $f: A \rightarrow B$ and a subset $X \subseteq A$, the image is: $f(X) = \{f(x) \mid x \in X\}$.
If we consider the entire domain, the image is the range: $\text{Image}(f) = f(A) = {f(a) \mid a \in A}$.
Pre-image of a Function
The pre-image refers to the set of all inputs that map to a particular output.
For a function $f: A \rightarrow B$ and $Y \subseteq B$, the pre-image is: $f^{-1}(Y) = \{x \in A \mid f(x) \in Y\}$.
For a single output value $y \in B$: $f^{-1}({y}) = \{x \in A \mid f(x) = y\}$.
For example, in the ordered pair $(1,2)$, $1$ is the pre-image of $2$ under the function.
Domain of a Function
The domain of a function is the set of all possible input values for which the function is defined.
If $f: A \rightarrow B$, then $A$ is the domain i.e. all the elements of set $A$ is called the Domain of the function.
Co-domain of a Function
The co-domain of a function is the set $B$ that includes all possible outputs, whether or not they are actually achieved by the function.
The range is always a subset of the co-domain and can sometimes be equal to it.
Range of a Function
The range of a function is the set of all actual output values corresponding to elements in the domain.
For example, for $f: A \rightarrow B$ where $f(x) = x^2$ and $A$ is the set of all integers, the range is:
$\{1, 4, 9, 16, \dots \}$.
Another example:
Let $A = \{1, 2, 3, 4, 5\}$ and $B = \{1, 4, 8, 16, 27, 64, 125\}$.
If $f(x) = x^3$, then:
Domain = $A$
Co-domain = $B$
Range = $\{1, 8, 27, 64, 125\}$.

The range is always a subset of the co-domain and the Range can be equal to the co-domain in some cases.
Representation of Relation and Function
In relations and functions, it’s important to understand how they can be visually or mathematically represented. Different forms (roster and set builder form) help in identifying patterns, solving problems, and understanding how elements from one set relate to another. Below are the common ways to represent relations and functions along with examples based on the topics covered in relations and functions class 12 and relations and functions examples.
1. Roster Form
In the Roster Form, relations and functions are written as a list of ordered pairs enclosed within curly brackets. Every pair explicitly shows how elements from set $A$ are connected to elements from set $B$.
Example:
Let $A = \{1, 2\}$ and $B = \{x, y\}$.
The relation is:
$R = \{(1, x), (2, y)\}$.
This is one of the easiest ways to represent relations and functions, especially for small sets.
2. Set Builder Form
The Set Builder Form uses a rule or condition to define the relationship between elements of sets, rather than listing all pairs. The symbols ‘:’ or ‘|’ are read as ‘such that’.
Example:
Let $A = \{1,2,3,4,5\}$ and $B = \{1,2,3,4,5,6,7,8,9\}$.
Define a function $f: A \rightarrow B$ by $f(x) = x + 1$.
Then the relation is written as:
$R = \{(x, y) : x \in A, y \in B \text{ and } y = x + 1\}$.
This form is widely used in relations and functions class 12 solutions where problems involve conditions or formulas.
3. Arrow Diagram
The Arrow Diagram visually represents how elements of set $A$ map to elements of set $B$. Arrows connect each element from the domain to its corresponding image in the codomain.
Example:
Let $A = \{1,2,3,4,5\}$ and $B = \{1,4,8,16,27,64,125\}$.
Define $f: A \rightarrow B$ as $f(x) = x^3$.
The diagram shows arrows mapping $1 \rightarrow 1$, $2 \rightarrow 8$, $3 \rightarrow 27$, and so on.
Arrow diagrams are useful when solving relations and functions class 12 important questions, making abstract concepts easier to understand.

4. Tabular Form
The Tabular Form is another way to represent relations and functions, where the elements of the domain and codomain are arranged in a table format. This makes it easier to visualize how each input corresponds to an output.
Example:
Let $A = \{1,2,3,4,5\}$ and $B = \{1,4,8,16,27,64,125\}$.
Define the function $f: A \rightarrow B$ by $f(x) = x^3$.
The table representing this function is:
| $x$ | $1$ | $2$ | $3$ | $4$ | $5$ |
| $f(x)$ | $1$ | $8$ | $27$ | $64$ | $125$ |
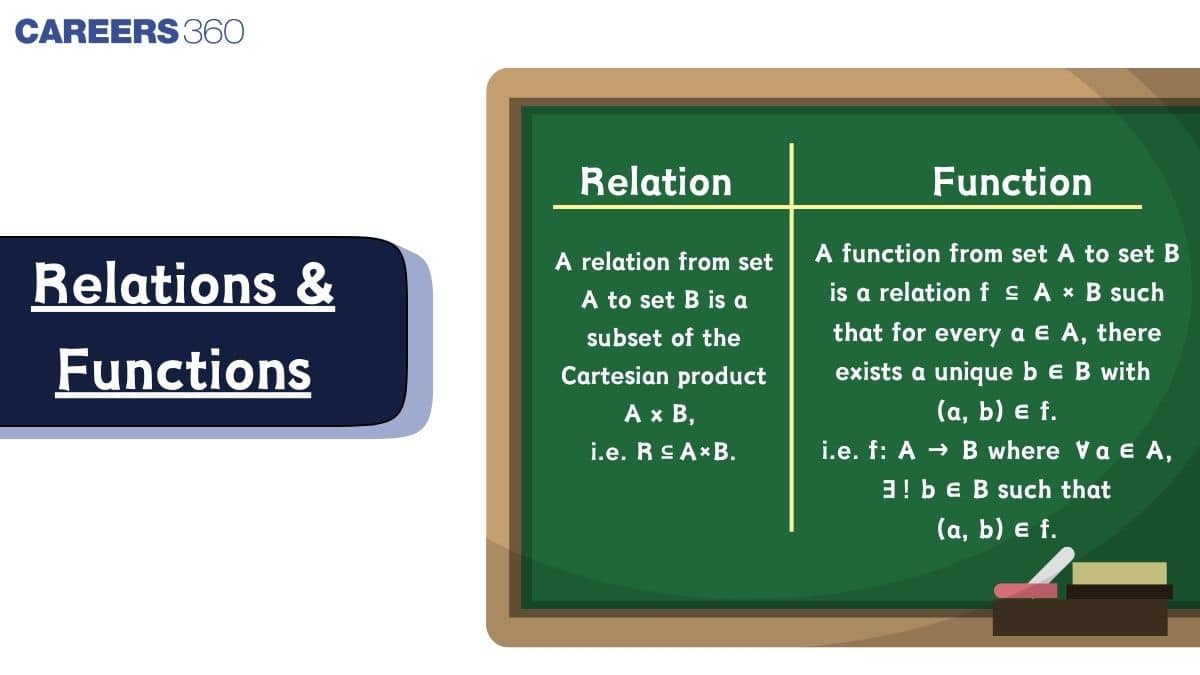
Difference Between Relations and Functions
| Aspect | Relations | Functions |
|---|---|---|
| Definition | A relation is a connection between elements of two sets. | A function is a relation where each element of set $A$ has exactly one image in set $B$. |
| Mapping | One element of set $A$ may be related to one or more elements of set $B$. | Each element of set $A$ is related to only one element of set $B$. |
| Representation | Can be shown using ordered pairs, set-builder, roster form, etc. | Represented in similar ways but with the condition that each input has a unique output. |
| Domain & Range | All first elements form the domain and all second elements form the range, without restrictions. | The domain is all inputs and each input is assigned a single output; the range is a subset of the codomain. |
| Example | $R = \{(1, x), (1, y), (2, z)\}$ | $f = \{(1, x), (2, y), (3, z)\}$ where each input has only one output. |
Types of Relations and Functions
In mathematics, relations and functions can be classified into various types based on the properties they possess. Understanding these types is important for solving problems in relations and functions class 12, relations and functions class 11, and for preparing for exams like JEE Main mathematics relations and functions.
1. Empty Relation
A relation $R$ on a set $A$ is called an empty relation if no element of $A$ is related to any element of $A$, i.e., $R = \emptyset$.
Example:
Let $A = \{2, 4, 6\}$ and $R = \{(a, b) : a, b \in A$ and $a + b$ is odd$\}$.
Here, $R$ contains no element, so it is an empty relation on $A$.
2. Universal Relation
A relation $R$ on a set $A$ is a universal relation if every element of $A$ is related to every other element of $A$, i.e., $R = A \times A$.
Example 1:
Let $A = \{2,4\}$ and $R = \{(2,2), (2,4), (4,2), (4,4)\}$.
Since $R = A \times A$, it is a universal relation.
Example 2:
Let $A = \{1,2,3\}$ and $R = \{(a, b) : |a - b| > -2, a, b \in A\}$.
Each ordered pair satisfies this condition, so $R$ is a universal relation.
3. Identity Relation
A relation where every element of $A$ is related to itself only is called an identity relation, denoted by $I_A$.
It is defined as: $R = \{(a, b) : a \in A, b \in A$ and $a = b\}$ or $I_A = \{(a, a) : a \in A\}$.
Example:
Let $A = {2,4,6}$. Then, $I_A = \{(2,2), (4,4), (6,6)\}$.
4. Reflexive Relation
A relation $R$ on set $A$ is reflexive if $(a, a) \in R$ for every $a \in A$.
Example:
Let $A = \{1,2,3\}$
$R_1 = \{(1,1), (2,2), (3,3)\}$
$R_2 = \{(1,1), (2,2), (3,3), (1,2), (2,1), (1,3)\}$
Both are reflexive relations, but$R_3 = \{(1,1), (2,2), (2,3), (3,2)\}$ is not reflexive because $(3,3)$ is missing.
5. Symmetric Relation
A relation $R$ is symmetric if whenever $a R b$ holds, then $b R a$ also holds for all $a, b \in A$.
Example:
Let $A = \{1,2,3\}$
$R_1 = \{(1,2), (2,1)\}$
$R_2 = \{(1,2), (2,1), (1,3), (3,1)\}$ are symmetric, while
$R_3 = \{(2,3), (1,3), (3,1)\}$ is not symmetric as $(3,2)$ is missing.
6. Transitive Relation
A relation $R$ is transitive if whenever $a R b$ and $b R c$ hold, then $a R c$ also holds for all $a, b, c \in A$.
Example:
Let $A = \{1,2,3\}$
$R_1 = \{(1,2), (2,3), (1,3), (3,2)\}$ is not transitive.
$R_2 = \{(2,3), (3,1)\}$ is not transitive.
$R_3 = \{(1,3), (3,2), (1,2)\}$ is transitive.
7. Equivalence Relation
A relation is an equivalence relation if it is reflexive, symmetric, and transitive.
Example:
Let $R = \{(1,1), (1,2), (2,1), (2,2)\}$.
Since $R$ satisfies all three properties, it is an equivalence relation.
8. Inverse Relation
An inverse relation swaps each ordered pair from a relation.
If $R \subseteq A \times B$, then
$R^{-1} = \{(b, a) : (a, b) \in R\}$.
Example:
Let $R = \{(1,2), (3,4)\}$.
Then, $R^{-1} = \{(2,1), (4,3)\}$.
Types of Functions
In mathematics, functions are classified into various types based on how elements from the domain relate to elements in the codomain. These types are essential for understanding concepts in relations and functions class 12, relations and functions examples, and solving problems in class 12 relations and functions important questions.
1. One-to-One Function (Injective)
A one-to-one function, also known as an injective function, is a function where every element in the domain has a unique image in the codomain. In other words, distinct elements of set $A$ are mapped to distinct elements in set $B$.
A function $f: X \rightarrow Y$ is called injective if different elements of $X$ always map to different elements of $Y$. That is, no two elements of set $X$ can have the same image.
Example:
Let $f: X \rightarrow Y$ be defined by $f(x) = x$, where
$X = \{-2, 2, 4, 6\}$ and $Y = \{-2, 2, 4, 6\}$.
Here, every element of $X$ has a distinct image in $Y$, so $f$ is a one-to-one function.

2. Many-to-One Function
A many-to-one function is a type of function where two or more elements from the domain are mapped to the same element in the codomain. This is a common scenario in problems related to relations and functions class 12, relations and functions examples, and relations and functions class 12 solutions.
A function $f: X \rightarrow Y$ is called many-to-one if two or more elements of set $X$ have the same image in set $Y$. That is, it is not a one-to-one function.
In other words, if $f: X \rightarrow Y$ is not injective, it is a many-to-one function.
Example:
In the case below, two elements $x_2$ and $x_3$ correspond to the same image $y_3$:
$f(x_2) = f(x_3) = y_3$.
A well-known example is the function:
$f(x) = x^2$
Domain: All real numbers $(\mathbb{R})$
Codomain: Non-negative real numbers $[0, \infty)$
Here, both $x$ and $-x$ have the same image, so it’s a many-to-one function.

3. Onto Function (Surjective)
A function $f: X \rightarrow Y$ is an onto function (or surjective) if every element of set $Y$ is the image of at least one element from set $X$. That is, Range = Codomain.
Example:
Let $X = \{x_1, x_2, x_3, x_4\}$ and $Y = \{y_1, y_2, y_3\}$,
then a function $f: X \rightarrow Y$ can be onto if every element in $Y$ is mapped to by some element from $X$.

4. Bijective Function
A function is bijective if it is both one-to-one and onto. Such functions create perfect pairings between the domain and codomain.
Example:
Let $X_1 = \{1, 2, 3\}$ and $X_2 = \{x, y, z\}$
A function $f: X_1 \rightarrow X_2$ is bijective if every element of $X_1$ maps uniquely to every element of $X_2$.

5. Odd and Even Functions
Let's describe about even and odd functions:
A function $f(x)$ is odd if $f(-x) = -f(x)$ for all $x$. Odd functions are symmetric about the origin.
A function is even if $f(-x) = f(x)$ for all $x$. Even functions are symmetric about the $y$-axis.
6. Identity Function
The function $f: \mathbb{R} \rightarrow \mathbb{R}$ defined by $f(x) = x$ for all $x$ is called the identity function.
Domain: $\mathbb{R}$
Range: $\mathbb{R}$
7. Constant Function
The function $f: \mathbb{R} \rightarrow \mathbb{R}$ defined by $f(x) = C$ where $C$ is a constant is a constant function.
Domain: $\mathbb{R}$
Range: ${C}$
8. Polynomial Function
A function $f: \mathbb{R} \rightarrow \mathbb{R}$ defined by
$f(x) = a_0 + a_1x + \dots + a_nx^n$
where $n \in \mathbb{N}$ and $a_0, a_1, ..., a_n \in \mathbb{R}$ is called a polynomial function.
9. Composite Function
Given functions $f: A \rightarrow B$ and $g: B \rightarrow C$, the composition $g \circ f$ is defined as: $g \circ f(x) = g(f(x))$ for all $x \in A$.

10. Rational Function
A rational function is of the form $\frac{f(x)}{g(x)}$, where $f(x)$ and $g(x)$ are polynomial functions and $g(x) \neq 0$.
Example:
$f(x) = \frac{x+1}{x+2}$, defined for $x \in \mathbb{R} - {-2}$.
11. Modulus Function
The modulus function is defined as:
$f(x) = |x| =
\begin{cases}
x, & x \geq 0 \\
-x, & x < 0
\end{cases}$
for all $x \in \mathbb{R}$.
Domain: $\mathbb{R}$
Range: $\mathbb{R}^{+} \cup {0}$
12. Signum Function
The signum function is defined as:
$f(x) =
\begin{cases}
1, & x > 0 \\
0, & x = 0 \\
-1, & x < 0
\end{cases}$
Domain: $\mathbb{R}$
Range: ${1, 0, -1}$
13. Greatest Integer Function
The greatest integer function is defined by $f(x) = [x]$, where $[x]$ is the largest integer less than or equal to $x$.
Example:
$f(x) = [x] = -1$ for $-1 \leq x < 0$,
$f(x) = [x] = 0$ for $0 \leq x < 1$, and so on.
14. Periodic Function
A function $f(x)$ is called periodic if there exists a positive real number $T$ such that $f(x+T) = f(x)$ for all $x$ in the domain. The smallest such $T$ is called the period.
Relations and Functions: Formulae and Operations
| Aspect | Algebra of Relations | Algebra of Functions |
|---|---|---|
| Definition | Relations are subsets of the Cartesian product $A × B$ | Functions are relations where each element of $A$ maps to a unique element of $B$ |
| Operations & Formulae | Union: $R ∪ S = \{(a,b) : (a,b) \in R \text{ or } (a,b) \in S\}$ Intersection: $R ∩ S = \{(a,b) : (a,b) \in R \text{ and } (a,b) \in S\}$ Difference: $R - S = \{(a,b) : (a,b) \in R \text{ and } (a,b) \notin S\}$ Composition: $R \circ S = \{(a,c) : \exists b \in B, (a,b) \in S \text{ and } (b,c) \in R\}$ Inverse: $R^{-1} = \{(b,a) : (a,b) \in R\}$ | Addition: $(f+g)(x) = f(x) + g(x)$ Subtraction: $(f-g)(x) = f(x) - g(x)$ Multiplication: $(f \cdot g)(x) = f(x) \cdot g(x)$ Division: $\left(\frac{f}{g}\right)(x) = \frac{f(x)}{g(x)}, g(x) \neq 0$ Composition: $(g \circ f)(x) = g(f(x))$ |
| Inverse | $R^{-1} = \{(b, a) : (a, b) \in R\}$ | $f^{-1}$ exists if $f$ is bijective, where $f(f^{-1}(x)) = x$ |
| Identity Element | $I_A = \{(a, a) : a \in A\}$ | $f(x) = x$ for all $x \in A$ |
| Properties | Reflexive, Symmetric, Transitive, Equivalence | Injective, Surjective, Bijective, Even, Odd, etc. |
| Examples | $R = \{(1, 2), (2, 3)\}, S = \{(2, 3), (3, 4)\}$ | $f(x) = x^2$, $g(x) = \sin x$, $h(x) = e^x$ |
List of Topics related to relations and functions according to NCERT/JEE MAIN
This section covers the list of topics related to relations and functions according to NCERT and JEE Main syllabus. It helps students focus on important concepts, examples, and formulas needed for class 11 and 12 preparation.
Recommended Books for Relations and Functions
This section provides a list of recommended books for relations and functions that are useful for class 11 and 12 students. These books cover concepts, examples, and practice questions aligned with NCERT and JEE Main syllabus.
| Book Name | Author / Publisher | Description |
|---|---|---|
| Mathematics for Class 11 & 12 | R.D. Sharma | Provides clear explanations, examples, and practice problems on relations, functions, and their applications. Suitable for school and competitive exams. |
| Higher Algebra | Hall & Knight | Covers advanced algebra topics including relations and functions, with detailed theory, solved examples, and exercises. Ideal for JEE aspirants. |
| Problems in Mathematics | V. Govorov, P. Dybov, N. Tikhomirov | A problem-solving approach with varied questions on relations and functions, helping build conceptual clarity and reasoning skills. |
| IIT Mathematics | M.L. Khanna | Provides chapter-wise problems, including algebraic operations on relations and functions, with solutions suited for JEE Main and Advanced. |
| Coordinate Geometry and Algebra | S.L. Loney | Classic text with in-depth discussions on sets, relations, and functions, as well as geometric interpretations. Excellent for both theory and practice. |
| NCERT Mathematics Books (Class 11 & 12) | NCERT | Official curriculum books offering step-by-step concepts, examples, and exercises aligned with school and competitive exams. Must-read for fundamentals. |
| Objective Mathematics | R.D. Sharma | Contains a variety of multiple-choice questions and short problems on relations and functions, helping with speed and accuracy for exams. |
| Comprehensive Mathematics for JEE Advanced | Tata McGraw Hill | Includes advanced-level problems and exercises on relations and functions with hints and solutions, suitable for competitive exam aspirants. |
NCERT Resources
In this section, you’ll find NCERT resources for Relations and Functions, including class 12 Maths notes, solutions, and exemplar problems. These are helpful for understanding concepts and practicing questions as per the NCERT syllabus.
NCERT Maths Notes for Class 12th Chapter 1 - Relations and Functions
NCERT Maths Solutions for Class 12th Chapter 1 - Relations and Functions
NCERT Maths Exemplar Solutions for Class 12th Chapter 1 - Relations and Functions
NCERT Subjectwise Resources
Explore NCERT subjectwise resources, including notes, solutions. These materials are designed to help class 12 students strengthen their understanding and prepare effectively for exams like JEE Main.
| Resource | Mathematics | Physics | Chemistry |
|---|---|---|---|
| NCERT Notes | NCERT notes Class 12 Maths | NCERT notes Class 12 Physics | NCERT notes Class 12 Chemistry |
| NCERT Solutions | NCERT solutions for Class 12 Mathematics | NCERT solutions for Class 12 Physics | NCERT solutions for Class 12 Chemistry |
Practice Questions Based on Relations and Functions
Practice questions based on Relations and Functions help students apply concepts, improve problem-solving skills, and master important topics for class 12 exams and competitive tests like JEE Main.
Frequently Asked Questions (FAQs)
A relation connects elements from two sets. The types of relation include empty relation, universal relation, identity relation, reflexive, symmetric, transitive, equivalence, and inverse relation, explained with examples in relations and functions class 12 solutions.
A relation in mathematics is a connection or association between elements of two sets. A relation $R$ from a non-empty set $A$ to a non-empty set $B$ is a subset of the cartesian product $A \times B$.
A relation from a set $A$ to a set $B$ is said to be a function from $A$ to $B$ if every element of set $A$ has one and only one image in set $B$.
The different ways to represent a funciton is roster form, set builder form, arrow diagram and tabular form.
To identify a function, check these two conditions.
(i) Every element in domain has a unique image in the co-domain.
(ii) No two elements in domain have the same image in the co-domain.
A relation from a set A to a set B is a subset of AB. As a result, a relation R is made up of ordered pairs (a,b), where aA and bB.
Yes, all functions are relations but not all relations are functions.