Roster and Set Builder Form
In everyday life, we often group similar things together, like colours, numbers, or names. In maths, this idea is called a set. A set is just a collection of items that belong together in some way. There are two methods used to represent sets: the roster form of a set and the set builder form. Whether you’re looking at an example of Sets, Roster and Set Builder form of Sets, understanding the examples and notation is crucial. This article explains roster form and set builder form examples, compares the two, and helps you confidently write in set builder form using the correct set builder notation in mathematics.
What is the Roster Form of a Set?
This Story also Contains
- What is Set Builder Form?
- Difference Between Roster Form and Set Builder Form
- How to convert roster form to set builder form?
- Solved Examples Based on Roster and Set Builder Form of Sets
- List of related topics to the Roster and Set Builder form of Sets
- NCERT Resources
- Practice Questions based on Roster and Set Builder form
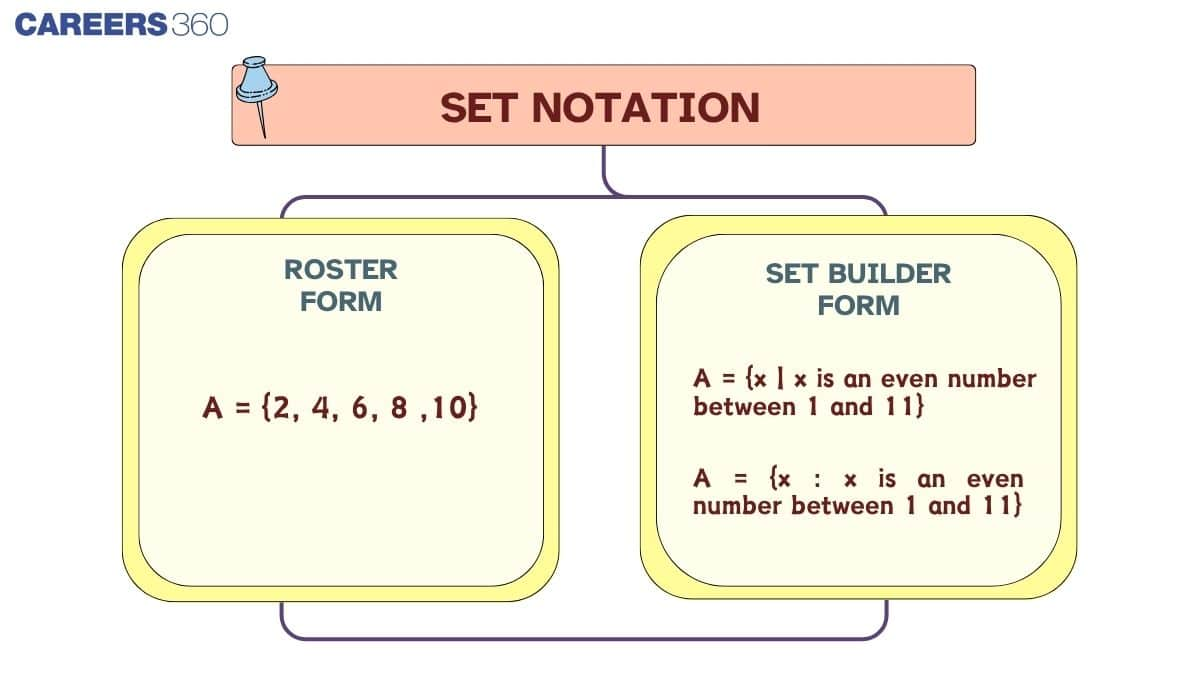
The roster form is one of the most commonly used methods to represent sets in mathematics. In this method, all the elements of a set are listed explicitly within curly brackets, separated by commas. It's simple, visual, and best used when the set has a finite and countable number of elements. We’ll explore the meaning, rules, and practical examples of roster form in detail below.
Definition and Meaning
The roster form of a set, also called roster notation, lists out each member of the set inside braces $\{\}$, with each element separated by a comma. This method works best when the number of elements is small and identifiable.
For example, the set of natural numbers less than 6 can be written as:
$A=\{1,2,3,4,5\}$
Key rules:
- Elements are not repeated.
- Order doesn’t matter.
- Each item is listed only once.
Example of Roster Form
Let’s look at some basic examples of sets in roster form:
- Vowels in the English alphabet:
$V = \{a, e, i, o, u\}$ - Natural numbers that divide 14:
$D = \{1, 2, 7, 14\}$ or $D = \{14, 2, 1, 7\}$ - Letters in the word "SCHOOL":
$L = \{S, C, H, O, L\}$
(No repetition of letters, even if they occur more than once.)
Roster Method Example in Daily Life
The roster form is not just for numbers or symbols. Here are some relatable daily-life uses:
- Set of colours in a rainbow:
$R = \{\text{Red}, \text{Orange}, \text{Yellow}, \text{Green}, \text{Blue}, \text{Indigo}, \text{Violet}\}$ - Favourite sports:
$S = \{\text{Cricket}, \text{Football}, \text{Tennis}\}$ - Subjects studied in Class 7:
$C = \{\text{Maths}, \text{English}, \text{Science}, \text{Social Studies}, \text{Hindi}\}$
What is Set Builder Form?
The set builder form is a compact way to represent sets using a rule or condition that describes the elements. Instead of listing all members one by one, this method specifies the property shared by all elements in the set. It’s especially useful when dealing with large or infinite sets. Let’s understand its definition, notation, and examples in detail below.
Definition and Meaning
In set builder form, we define a set by stating the condition that every element must satisfy. This method avoids repetition and makes sets more concise, especially when the pattern among elements is clear.
For instance, if set $Z$ contains all values of $x$ that satisfy a condition $q(x)$, we write:
$Z = \{x : q(x)\}$ or $Z = \{x \mid q(x)\}$
Here, the symbol “:” or “|” is read as “such that”.
Example:
The set $A = \{0, 1, 8, 27, 64, \dots\}$ can be written in set builder form as:
$A = \{x^3 : x \text{ is a non-negative integer}\}$
Set Builder Notation
Set builder notation uses curly braces ${ }$ to enclose the rule that defines the set. It typically follows the structure:
$\{x : \text{condition on } x\}$ or $\{x \mid \text{condition on } x\}$
Key notations:
“:” or “|” means “such that”
The condition explains what values $x$ can take
This notation helps us represent sets in a structured and logical way without listing each element.
Set Builder Form Examples
Here are some examples of sets written in set builder form:
- Set of even natural numbers less than 20:
$E = \{x : x \text{ is an even natural number and } x < 20\}$ - Set of letters in the word "APPLE":
$L = \{x : x \text{ is a letter in the word APPLE}\}$
(In roster form, this would be $L = \{A, P, L, E\}$) - Set of natural numbers divisible by 5 up to 50:
$A = \{x : x \text{ is a natural number } \leq 50 \text{ and divisible by } 5\}$
Using Set Builder Notation
To use set builder notation properly:
- Identify the common property among all elements.
- Express that condition clearly using mathematical or word-based rules.
- Avoid listing individual elements, focus on the rule.
Tip: When converting from roster to set builder form, look for a pattern or rule the elements follow.
Example (conversion from roster to builder):
Roster: $A = \{5, 10, 15, 20, 25, 30, 35, 40, 45, 50\}$
Builder: $A = \{x : x \text{ is a natural number } \leq 50 \text{ and divisible by } 5\}$
Likewise, when converting from builder to roster form, just apply the condition to list elements:
Builder: $B = \{x : x \text{ is a letter in the word APPLE}\}$
Roster: $B = \{A, P, L, E\}$
Set builder form is a powerful way to represent infinite or patterned sets in a compact and logical format.
Difference Between Roster Form and Set Builder Form
What is the roster method of set builder? What is set builder form? These are the common questions about the sets. Both roster form and set builder form are useful methods to represent sets, but they serve different purposes based on the nature of the set and the clarity needed. While roster form focuses on listing elements directly, set builder form describes the set using a property or rule. Below, we break down their key differences.
The table below highlights the main differences between roster form and set builder form:
Feature | Roster Form | Set Builder Form |
Definition | Lists all elements of the set explicitly | Describes elements using a rule or condition |
What is the difference between roster and set-builder notation? | ||
Notation Used | Elements inside curly braces, separated by commas | Uses symbols like “:” or “|” |
Example | $A=\{2,4,6,8,10\}$ | $A=\{x:x \text{is an even number less than} 12\}$ |
Best Used For | Finite and small sets with known elements | Infinite sets or sets with a clear pattern |
Repetition of Elements | Not allowed | Not applicable as elements are not listed individually |
Order of Elements | Doesn’t matter | Order is irrelevant as elements are defined, not listed |
Clarity of Elements | Instantly visible | Needs interpretation of the condition |
When to Use Each Form
Choosing between roster form and set builder form depends on the nature of the set:
- Use roster form when:
- The set has a limited number of elements
- All elements are clearly known and countable
- You want a quick visual representation
Example: $B=\{1,3,5,7,9\}$
- Use set builder form when:
- The set is infinite or follows a clear rule or pattern
- You want to define the condition without listing each element
- The elements are too many to write individually
Example: $C=\{x:x \text{ is a multiple of }3\}$
Understanding when and how to use each form helps in representing sets efficiently and accurately in different mathematical problems.
How to convert roster form to set builder form?
Converting from roster form to set builder form involves identifying the underlying pattern or condition that all elements in the set follow. Instead of listing every element, the set builder form expresses the logic behind the set, making it more compact, especially when dealing with long or infinite sets. Let’s understand how to make this conversion with simple steps and examples.
Follow these steps to convert a set from roster form to set builder form:
- List the Set in Roster Form
Start with the given set written in roster form.
Example: $A=\{5,10,15,20,25,30\}$ - Observe the Pattern
Identify what is common among all elements.
In this case, every number is a multiple of 5. - Frame the General Rule
Express this rule using a variable like x and write the condition clearly.
Example: x is a natural number divisible by 5 and less than or equal to 30 - Write the Set in Set Builder Form
$A = \{x : x \text{ is a natural number, } x \leq 30 \text{, and divisible by } 5\}$
Roster Form to Set Builder Form Questions
Here are a few practice questions where you need to convert from roster to set builder form:
1. Convert $P = \{2, 4, 6, 8, 10\}$
$P = \{x : x \text{ is an even natural number and } x \leq 10 \}$
2. Convert $Q = {1, 4, 9, 16, 25\}$
$Q = \{x^2 : x \text{ is a natural number and } x \leq 5 \}$
3. Convert $R = \{3, 6, 9, 12, 15, 18\}$
$R = \{x : x \text{ is a multiple of 3 and } x \leq 18\}$
Solved Examples Based on Roster and Set Builder Form of Sets
These examples will help you learn how to write sets in both roster form and set builder form, along with explanations on how to identify patterns and convert between the two.
Question 1: Which of the following is not a set?
1) The collection of all licensed drivers in the class.
2) The collection of students in class above the age 15.
3) The collection of all the young students in the class.
4) The collection of all students with names starting from 'A'.
Solution:
A set is a well-defined collection of objects.
In this question,
"The collection of young students" is not a set because the term young is not well defined.
In all other options, we can identify the elements present in those collections, so they are sets.
Hence, the answer is option 3.
Question 2: Which of the following sets has an infinite number of elements?
1) $A=\{x:x \text{ is an odd number on dice} \}$
2) $B=\{x:x \text{ is a prime number} \}$
3) $C=\{x:x \text{ is a factor of }24\}$
4) $D=\{x:x \text{ is an even prime number} \}$
Solution:
Option 1$=\{1,3,5\}$: so a finite number of elements.
Option 2$=\{2,3,5,7,……\}$ : so infinite number of elements.
Option 3$=\{1,2,3,4,6,8,12,24\}$: so a finite number of elements.
Option 4$=\{2\}$: so a finite number of elements.
Hence, the answer is option 2.
Question 3: Which of the following is a set?
1)The list of all the bright colours.
2)The list of all the dull colours.
3)The list of all colours in the Rainbow.
4)The list of all the good colours
Solution:
As we learnt,
A set is a well-defined collection of objects. eg. $A=\{1,2,3\}$
In this Question,
Bright, dull and good colours are not well-defined as it is different for different people. But the list of all colours in the rainbow is definite and well-defined. So, it is a set.
We can decide with respect to any colour, say green, whether it will lie in the set or not. So, it is a well-defined collection. We cannot do this in case of bright, dull or good colours.
Hence, the answer is option 3.
Question 4: Roster form of the set $\{p^2:p=2q,1<q<3,p \in N\}$ :
1) $\{3, 4, 5\}$
2) $\{9, 16, 25\}$
3) $\{4\}$
4) None of these
Solution:
$1 < q < 3 \implies 2 < 2q < 6$, let $p = 2q$ and $p \in \mathbb{N}$
So, $p = 3, 4, 5$
$p^2 = 9, 16, 25 \implies$ Set is $\{9, 16, 25\}$
Hence, the answer is option (2).
Question 5: Which of these sets are written in the Roster Form?
1) $A = \{x : x \text{ is a vowel}\}$
2) $B = \{a, e, i, o, u\}$
3) $C = \{x : 1 < x < 2, x \text{ is a natural number}\}$
4) $D = \{x : x \text{ is an even number}\}$
Solution:
As we learnt, in roster form, all the elements of a set are listed, and the elements are separated by commas and are enclosed within braces $\{ \}$.
Option 2 is written in roster form.
Hence, the answer is option 2.
List of related topics to the Roster and Set Builder form of Sets
To deepen your understanding of the Roster and Set Builder forms of Sets, it's essential to explore the related foundational concepts in set theory. Topics such as Equal and Equivalent Sets, Empty Set, Subsets, Finite and Infinite Sets, Singleton Set, Power Set, and Universal Set are closely connected and frequently used together in problems. Mastering these will enhance your ability to interpret and represent sets with clarity and accuracy.
NCERT Resources
Explore a complete set of NCERT resources for Class 11 Mathematics Chapter 1 – Sets. This section includes concise notes, detailed NCERT textbook solutions, and challenging exemplar problems with answers. Whether you're revising key concepts or practising for exams, these materials offer a solid foundation to master the topic of Sets effectively.
NCERT Class 11 Mathematics Chapter 1 - Sets Notes
Practice Questions based on Roster and Set Builder form
Boost your understanding of the roster form and set builder form with these quick practice questions. From set builder form examples to roster form of set examples, these exercises help you apply builder notation, spot patterns, and confidently write in set builder form.
Sets, Roster and Set Builder Form Of Sets - Practice Question MCQs
Practice questions on the next topics of the Sets:
You can test yourself on the topics based on different types of sets, subsets, and properties of sets. These MCQs cover important concepts of sets along with their important properties and will help in revision and concept clarity.
Intersection of Set, Properties of Intersection - Practice Question MCQs |
Complement of a set, Law of Complement, Property of Complement - Practice Question MCQs |
Frequently Asked Questions (FAQs)
It is a mathematical notation for describing a set by representing its elements or explaining the properties that its members must satisfy. For example, For the given set A=...,−3,−2,−1,0,1,2,3,4, the set builder notation is A=x∈ℤ|x≤4.
Then 2,4,6,8,10…… are even natural numbers. So, the set builder of the given set is {x:x is an even natural number}
Given Set A=2,3,5,7,11. In set builder form, it may be written as ; A={a∈N:a is prime &1<a<12}
The set B={1,2,3,6,9,18} can be written in the set builder form as. B={All factors of 18 } B={x|x is a multiple of 3}, B is the set of all factors of 18.
It is a representation of a set that lists all of the elements in the set, separated by commas, within braces.