Difference of Set: Definition, Formula, Properties, Examples
The difference of sets is a fundamental concept in set theory that helps students understand how to identify elements that belong to one set but not the other. This operation is commonly used in mathematics to compare data sets, solve Venn diagram problems, and analyze relationships between groups of items. Learning the difference between two Sets in mathematics is especially useful for students preparing for exams where set operations are frequently tested. It also builds a strong base for advanced topics in algebra, logic, and data handling. For example, if a teacher wants to identify students who passed science but failed math, they would take the difference between the set of students who passed science and those who passed math. In this article, we will explain the definition, notation, examples, and properties of the difference of sets in a simple and clear way.
This Story also Contains
- What is the Difference of Sets?
- Difference of Sets: Examples
- Difference of Sets: Venn Diagram
- Properties of the Difference of Sets
- Symmetric Difference of Sets $(A \Delta B)$
- Solved Examples Based On the Difference of Sets
- List of Topics Related to the Difference of Sets
- NCERT Resources
- Practice Questions on Difference of Sets
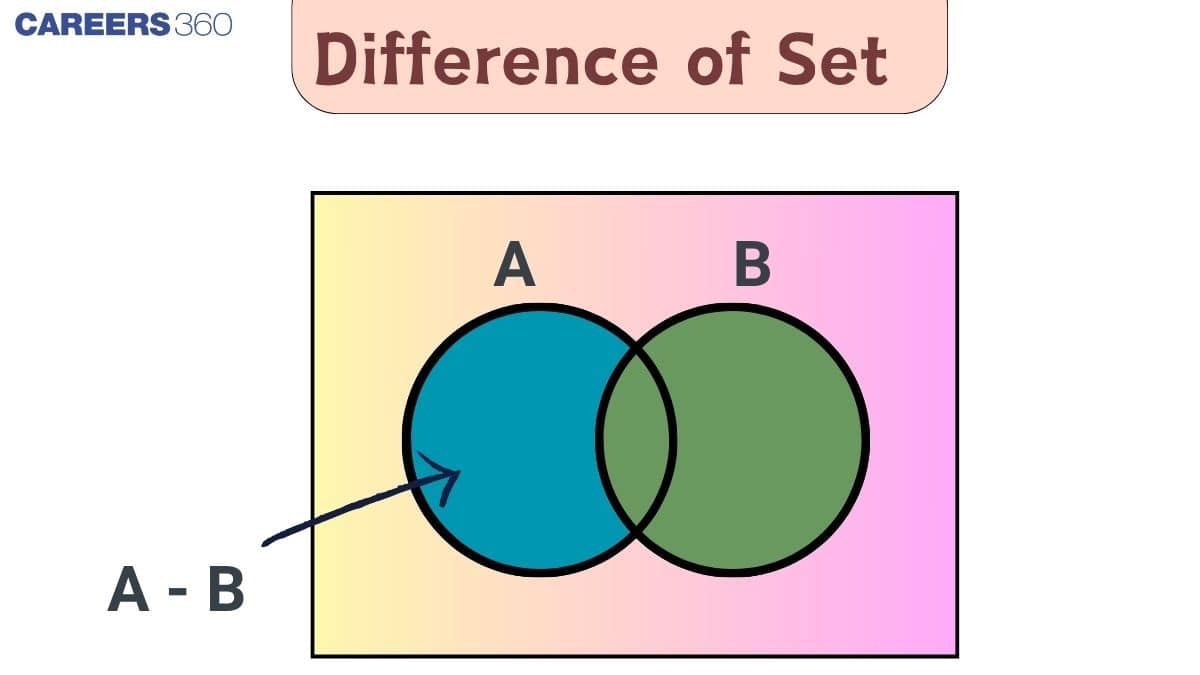
What is the Difference of Sets?
The difference of sets is one of the fundamental operations in set theory. It plays an important role in topics that involve separating or excluding specific categories of elements from a group. Before we explore the difference of sets in detail, it is important to understand what sets are.
Difference of Sets: Definition
The difference of two sets $A$ and $B$ (in that order) refers to the set of elements that are present in $A$ but not in $B$.
Symbolically, this is written as:
$A - B$, which is read as “A minus B.”
How to Find the Difference of Sets?
To find the difference between two sets, follow these steps:
- Identify the given non-empty sets and express them in set-builder or roster form.
- Determine the order of the difference operation, whether you are finding $A - B$ or $B - A$.
- Find the intersection of the sets: $A \cap B$.
- Remove the elements of $A \cap B$ from Set $A$.
- The remaining elements in Set $A$ form a new set, denoted as $A - B$.
Thus, $A - B$ is the set of all elements that belong to $A$ but not to $B$.
Now, let us look into difference of set example for better understanding.
Difference of Sets: Examples
Understanding the difference between two sets with examples helps solidify the concept and shows how to apply it in real problems. Below are a few well-explained examples using both numbers and real-world categories.
Example 1:Let $A = \{1, 2, 3, 4\}$ and $B = \{4, 5, 6, 8\}$
Then:
$A - B = \{1, 2, 3\}$ (Elements in $A$ but not in $B$)
$B - A = \{5, 6, 8\}$ (Elements in $B$ but not in $A$)
Example 2:
Let $A = \{\text{blue, violet, green, yellow, black, white, red}\}$
and $B = \{\text{black, blue, red, grey, brown}\}$
Then:
$A - B = \{\text{violet, green, yellow, white}\}$
$B - A = \{\text{grey, brown}\}$
Example 3:
Let $A = \{x : x \in \mathbb{N} \text{ and } x \leq 10\}$
and $B$ = set of all integers greater than $-5$ and less than or equal to $5$
Now,
$A = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}$
$B = \{-4, -3, -2, -1, 0, 1, 2, 3, 4, 5\}$
Then:
$A - B = \{6, 7, 8, 9\}$
$B - A = \{-4, -3, -2, -1, 0\}$
Example 4:
Let $A$ = set of all even natural numbers less than $10$
Let $B = \{2, 4, 6, 8\}$
Now, $A = \{2, 4, 6, 8\}$ and $B = \{2, 4, 6, 8\}$
Then:
$A - B = \phi$
$B - A = \phi$
These difference of set examples show how to subtract elements from one set based on the presence of those elements in another set. In each case, only the non-common elements remain in the resulting set.
Difference of Sets: Venn Diagram
The difference of sets Venn diagram visually represents the elements that belong to one set but not to another. When we write $A - B$, it means we are looking for all the elements in Set $A$ that are not present in Set $B$.
This concept is best understood with the help of a Venn diagram, where overlapping areas show common elements, and the shaded part represents the set difference.
Example Using Venn Diagram:
Let $A = \{1, 2, 3, 4\}$ and $B = \{4, 5, 6, 8\}$.
From the Venn diagram:
- The overlapping part (i.e., $A \cap B$) is $\{4\}$
- The difference $A - B$ includes elements in $A$ but not in $B$, which is $\{1, 2, 3\}$
- Similarly, $B - A$ includes elements in $B$ but not in $A$, which is $\{5, 6, 8\}$
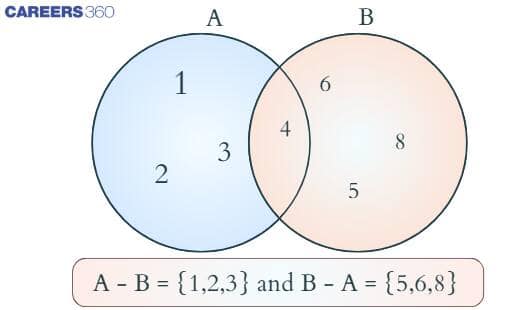
Thus, the Venn diagram for the difference of sets clearly shows how the common element is excluded from the result, helping learners visually understand the subtraction between sets.
Properties of the Difference of Sets
Understanding the properties of difference of sets in mathematics helps clarify how this operation behaves under different conditions. These properties are useful in solving problems related to set operations, Venn diagrams, and logical reasoning.
Here are the key properties of set difference:
- Non-Commutative Property:
In general, $A - B \ne B - A$.
This means that set difference is not commutative, and the order of subtraction matters. - Identity Property with Same Set:
The difference of a set with itself is always the empty set:
$A - A = \phi$ or $\phi$ - Difference with Empty Set:
The difference of any finite set with the null set gives the original set:
$A - \phi = A$ - Difference with Universal Set:
The difference of a set with the universal set results in the empty set:
$A - U = \phi$ (Since all elements of $A$ are already included in $U$) - Mutually Disjoint Results:
The sets $A - B$, $A \cap B$, and $B - A$ are all mutually disjoint, meaning:- $(A - B) \cap (A \cap B) = \phi$
- $(A - B) \cap (B - A) = \phi$
- $(A \cap B) \cap (B - A) = \phi$


Symmetric Difference of Sets $(A \Delta B)$
The symmetric difference of sets refers to the set of elements that belong to either set $A$ or set $B$ but not to both. In other words, it excludes the common elements.
The symmetric difference of two sets $A$ and $B$ is defined as:
$A \Delta B = (A - B) \cup (B - A)$
Alternatively, it can also be represented as:
$A \Delta B = (A \cup B) - (A \cap B)$
This operation is useful in identifying non-overlapping elements between sets and is commonly applied in data filtering, logic circuits, and set-based problem-solving.
How to Find Symmetric Difference of Sets
To find the symmetric difference between two sets, follow these simple steps:
- Identify the given non-empty sets and express them in set-builder or roster form.
- Find the difference $A - B$ (elements in $A$ but not in $B$).
- Find the difference $B - A$ (elements in $B$ but not in $A$).
- Take the union of both differences: $A \Delta B = (A - B) \cup (B - A)$
Symmetric Difference of Sets – Examples
Example 1:
Let $A = \{1, 2, 3, 4\}$ and $B = \{4, 5, 6, 8\}$
Then:
$A - B = \{1, 2, 3\}$,
$B - A = \{5, 6, 8\}$
So, $A \Delta B = \{1, 2, 3, 5, 6, 8\}$
Example 2:
Let $A = \{\text{blue, violet, green, yellow, black, white, red}\}$
and $B = \{\text{black, blue, red, grey, brown}\}$
Then:
$A - B = \{\text{violet, green, yellow, white}\}$
$B - A = \{\text{grey, brown}\}$
So, $A \Delta B = \{\text{violet, green, yellow, white, grey, brown}\}$
Example 3:
Let $A = \{x \in \mathbb{N} \mid x \leq 10\}$
Let $B$ = set of all integers greater than $-5$ and less than or equal to $5$
Now,
$A = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}$
$B = \{-4, -3, -2, -1, 0, 1, 2, 3, 4, 5\}$
Then:
$A - B = \{6, 7, 8, 9\}$
$B - A = \{-4, -3, -2, -1, 0\}$
So, $A \Delta B = \{6, 7, 8, 9, -4, -3, -2, -1, 0\}$
Example 4:
Let $A$ = set of all even natural numbers less than $10$
Let $B = {2, 4, 6, 8}$
Then:
$A = {2, 4, 6, 8}$, $B = {2, 4, 6, 8}$
$A - B = \phi$, $B - A = \phi$
So, $A \Delta B = \phi$
Symmetric Difference of Sets – Venn Diagram
The symmetric difference of sets Venn diagram shows the regions of both sets $A$ and $B$ excluding their intersection. The shaded areas represent elements that are either in $A$ or in $B$, but not in both.
For instance, let $A = \{1, 2, 3, 4\}$ and $B = \{4, 5, 6, 8\}$
Then:
- $A \cap B = \{4\}$ (common element)
- $A \Delta B = \{1, 2, 3, 5, 6, 8\}$ (all non-common elements)
The Venn diagram will shade only the non-overlapping parts of the two circles, clearly illustrating the symmetric difference.
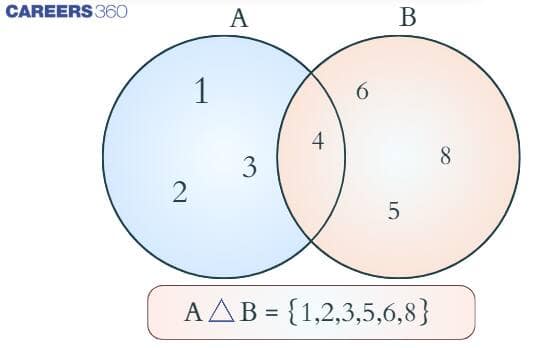
Solved Examples Based On the Difference of Sets
Example 1: If $\mathbf{A}, \mathbf{B}$, and $\mathbf{C}$ are non-empty sets, then $(A-B) \cup(B-A)$
1) $(A \cup B)-B$
2) $A-(A \cap B)$
3) $(A \cup B)-(A \cap B)$
4) $(A \cap B) \cup(A \cup B)$
Solution:
Clearly, as the sets in the question and in the third option, both equal the symmetric difference of $A$ and $B$, so both these are equal.
$(A-B) \cup(B-A)=(A \cup B)-(A \cap B)$
Hence, the answer is the option 3.
Example 2: If $\mathrm{A}, \mathrm{B}, \mathrm{C}$ are any three sets,then $A-(B \cup C)$ is equal to?
Option 1) $(A-B) \cup(A-C)$
Option 2) $(A-B) \cap(A-C)$
Option 3) $(A-B) \cup C$
Option 4) $(A-B) \cap C$
Solution:
The difference of the sets $A$ and $B$ in this order is the set of elements which belong to $A$ but not to $B$ wherein Symbolically, we write A - B and read as "A minus B".
According to De Morgan's laws
$A-(B \cup C)=(A-B) \cap(A-C)$
Hence the answer is option 2.
Example 3: Let $\mathrm{A}, \mathrm{B}$, and $\mathbf{C}$ be sets such that $\phi \neq A \cap B \subseteq C$. Then which of the following statements is not true?
1) $B \cap C \neq \phi$
2) If $(A-B) \subseteq C$, then $A \subseteq C$
3) $(C \cup A) \cap(C \cup B)=C$
4) If $(A-C) \subseteq B$, then $A \subseteq B$
Solution:
$ \begin{aligned} & \text { As }(A \cap B) \subseteq C \\ & \Rightarrow(A \cap B) \subseteq(B \cap C) \\ & \text { as }(A \cap B) \neq \phi_{\Rightarrow}(B \cap C) \neq \phi \end{aligned} $
So, option (1) is true
Let $x \in A$ and $x \notin B \Rightarrow x \epsilon(A-B)_{\Rightarrow} \Rightarrow x \epsilon C$ let $x \in A$ and $x \epsilon B \Rightarrow x \epsilon(A \cap B) \Rightarrow x \epsilon C$ Hence $x \in A$ and $x \in C \Rightarrow A \subseteq C$ So, option (2) is true.
Let $\begin{aligned} & x \in C, x \in(C \cup A) \cap(C \cup B)) \\ & =>x \epsilon(C \cup A) \text { and } x \epsilon(C \cup B)) \\ & (x \in C \text { or } x \in A) \text { and }(x \in C \text { or } x \in B) \\ & =>x \epsilon C \text { or } x \epsilon(A \cap B) \\ & =>x \epsilon C \quad A s, A \cup B \subseteq C\end{aligned}$
$\begin{aligned} &(C \cup A) \cap(C \cup B) \subseteq C.......\text { (1) } \end{aligned}$
Now,$ \begin{aligned} & =>x \epsilon C \\ & =>x \epsilon(C \cup A) \cap(C \cup B) \\ & =>C \subseteq(C \cup A) \cap(C \cup B) ......(2) \end{aligned} $
From (1) and (2
$(C \cup A) \cap(C \cup B)=C$
=> Option (3) is correct.
For $\mathrm{A}=\mathrm{c}, A-C=\phi$
$=>\phi \subseteq B \text { but }=>A \nsubseteq B$
So, option (4) is not true.
Example 4: If $A \subset B$, then $A-B=$
1) A
2) B
3) $A \cap B$
4) $\phi$
Solution:
If A is subset of B , then Venn diagram looks something like this:
![]()
![]()
![]()
Clearly, $\mathrm{A}-\mathrm{B}=\phi$, as all elements of A are present in B .
List of Topics Related to the Difference of Sets
To fully understand the difference of sets, it's important to explore related concepts in set theory. This section lists key topics that build the foundation for mastering set operations and their applications.
NCERT Resources
Explore essential NCERT study resources for Class 11 Sets, including detailed solutions, clear revision notes, and carefully selected exemplar problems. These materials are designed to strengthen your understanding and help you prepare confidently for board exams and competitive tests.
NCERT Solutions for Class 11 Chapter 1 Sets
Practice Questions on Difference of Sets
Regular practice is key to mastering the difference of sets and its related operations. Below, you'll find a set of practice questions designed to test your understanding of definitions, formulas, properties, and real-world applications of set difference. Use these exercises to build accuracy and confidence.
To practice questions based on Difference Of Set - Practice Question MCQ, click here.
You can practice the next topics of Sets below:
| Complement Of A Set Law Of Complement Property Of Complement - Practice Question MCQ |
| Ordered Pair Cartesian Product Of Two Sets - Practice Question MCQ |
Frequently Asked Questions (FAQs)
No, $A-B$ is not equal to $B-A$.
The set difference of set A with null set is $A-\{\} = A$.
The symmetric difference of two sets $A$ and $B$ is defined as
$A \Delta B=(A-B) \cup(B-A)$. The symmetric difference of set A and B can also represented as $A Δ B = ( A ∪ B) - ( A ∩ B )$
The intersection of any two of these sets is the null set is called a disjoint set.
The difference of set definition is, $A-B$ in this order is the set of elements that belong to $A$ but not to $B$.