Cardinal Numbers - Meaning, Examples, Sets
Understanding the cardinal number of a set is a crucial part of learning set theory in mathematics. It refers to the total number of distinct elements present in a set and helps in comparing the sizes of different sets. Whether you're working with finite sets, empty sets, or infinite sets, knowing how to calculate their cardinality is essential for solving problems related to counting, probability, and relations. This topic often appears in board exams and competitive tests, making it important for students to build a strong foundation. In this article, you’ll learn everything you need to know about the cardinal number of some sets with clear examples and explanations.
This Story also Contains
- Cardinal Number of Set
- Cardinal Numbers of Sets Formula
- Difference between Cardinal and Ordinary Numbers
- Solved Examples Based On the Cardinal Number of Sets
- List of Topics Related to Cardinal Numbers of Some Sets
- NCERT Resources
- Practice Questions on Cardinal Number of a Set
Cardinal Number of Set
A set is a well-defined collection of distinct objects or elements. These objects can be anything—numbers, letters, people, or even other sets. In set theory, sets are denoted by capital letters such as $A, B, C, S, U, V$, etc., and are widely used in mathematics to represent groups of objects sharing common properties. Now, let's explore an important concept within set theory: the cardinal number of a set.
What is the Cardinal Number of a Set?
In mathematics, the cardinal number of a set refers to the total number of distinct elements in that set. It helps quantify the size or count of a set and is especially useful when working with finite sets.
For example, in a cricket team, there are 11 players. The number $11$ represents the cardinal number of the set of players in the team.
The cardinal number of a set $A$ is denoted by $n(A)$.
If $A = \{1, 3, 7, 11, 13\}$, then the number of elements in $A$ is:
$n(A)=5$
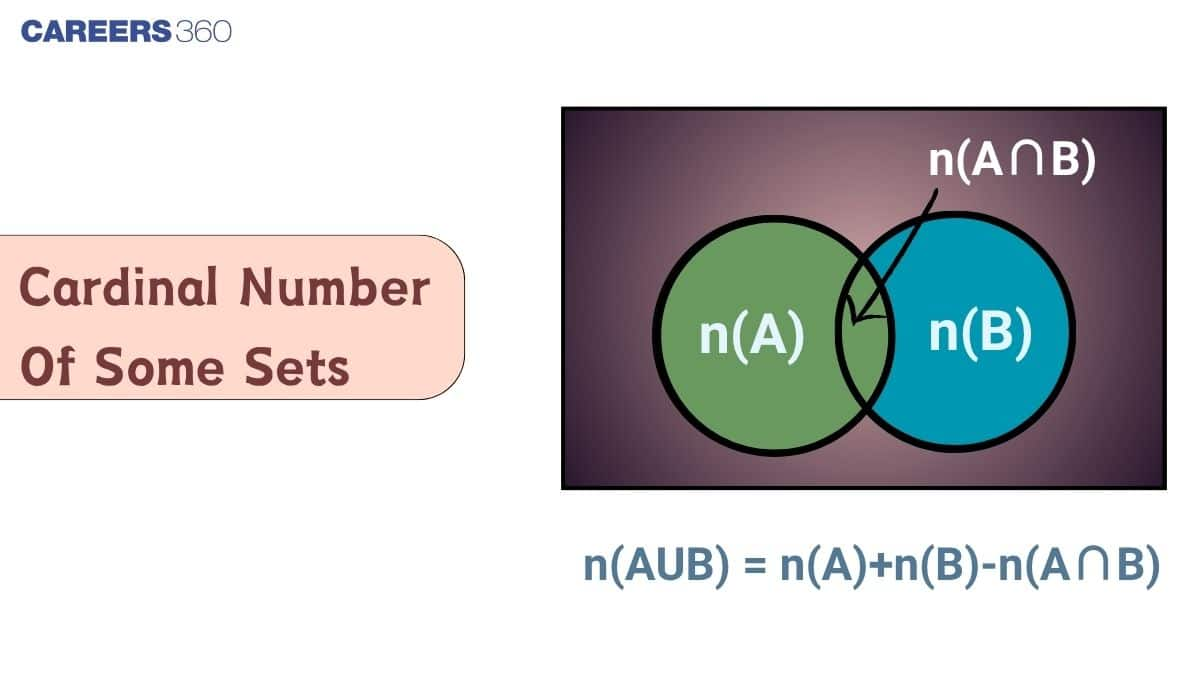
Formula for Cardinal Number of the Union of Two Sets
Given two finite sets $A$ and $B$, the number of elements in their union of sets is given by the formula:
n(A∪B)=n(A)+n(B)−n(A∩B)n(A \cup B) = n(A) + n(B) - n(A \cap B)n(A∪B)=n(A)+n(B)−n(A∩B)
If $A$ and $B$ are disjoint sets (i.e., $A \cap B = \varphi$), then:
$n(A \cup B) = n(A) + n(B)$
Formula for Cardinal Number of the Union of Three Sets
If $A$, $B$, and $C$ are any three finite sets, then the number of elements in their union is given by the inclusion-exclusion principle:
$n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(A \cap C) + n(A \cap B \cap C)$
This formula helps avoid overcounting the elements that appear in more than one set.
Cardinal Number Notation and Terminology
- Symbol: $n(A)$ represents the cardinal number of set $A$.
- Finite set: A set with a countable number of elements.
- Infinite set: A set with elements that cannot be counted (like natural numbers).
- Empty set: The cardinal number of the empty set $\varphi$ is $0$, i.e., $n(\varphi) = 0$.
Now that you've understood what the cardinal number of a set is, let’s go through some examples of the cardinal number of sets to reinforce the concept and practice applying the formulas.
Cardinal Number of Some Sets Examples
Understanding the cardinal number becomes easier through simple examples. Here are a few sets with their corresponding cardinal numbers, calculated by counting the number of distinct elements in each set:
- Let $A = \{1, 2, 6, 7, 4, 3, 5, 2, 8\}$
Since each element is counted only once, even if repeated:
$\Rightarrow n(A) = 8$ - Let $B = \{a, d, c, t, r, v\}$
All elements are unique:
$\Rightarrow n(B) = 6$ - Let $C = \{\}$ (an empty set)
No elements in the set:
$\Rightarrow n(C) = 0$
- Let $D = \{x, x, x, x\}$
All elements are the same, so only one distinct element:
$\Rightarrow n(D) = 1$ - Let $E = \{apple, mango, banana, mango, orange\}$
Remove duplicate "mango":
$\Rightarrow n(E) = 4$
Cardinal Numbers of Sets Formula
To calculate the number of elements in sets, especially when they are disjoint or overlapping, we use specific cardinal number formulas. These formulas help in solving set problems efficiently in exams and real-life situations. Below are the standard formulas used for two or three sets:
For Two Sets:
- If sets are disjoint (no common elements):
$n(A \cup B) = n(A) + n(B)$ - If sets are overlapping (some common elements):
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
For Three Sets:
- If sets are disjoint:
$n(A \cup B \cup C) = n(A) + n(B) + n(C)$ - If sets are overlapping:
$n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(C \cap A) + n(A \cap B \cap C)$
Important Notes on Cardinal Numbers:
- The collection of all ordinal numbers can be represented using cardinal numbers.
- Cardinal numbers can be expressed in words, such as one, two, three, etc.
- While cardinal numbers indicate "how many" elements are present in a set, ordinal numbers tell us the position or order (like first, second, third).
Difference between Cardinal and Ordinary Numbers
Cardinal numbers and ordinal numbers are both types of numbers used in mathematics and counting. Cardinal numbers represent the quantity or amount of objects or elements in a set, while ordinal numbers indicate the position or order of objects in a sequence. For example, the cardinal number "three" represents the quantity of three objects, while the ordinal number "third" indicates the position of an object in a sequence. While cardinal numbers are used for counting and measuring, ordinal numbers are used for ranking and ordering.
| Cardinal numbers | Ordinal numbers |
They are counting numbers that represent quantity. | They are based on the rank or position of an object in a given list or order. |
Cardinal numbers give us the answer of 'how many?'. | Ordinal numbers give us the answer of 'where'. For instance, where does the object lies in the list? |
Examples are 1, 2, 3, 4,5, 10, etc. | Examples are 1st, 2nd, 3rd, 4th, 5th, 10th, etc. |
Solved Examples Based On the Cardinal Number of Sets
Example 1: If $U$ is the universal set, $n(A)=50, n(B)=60$, and $n(A \cap B)=30$. The total elements in the universal set is 200. Find $n\left(A^{\prime} \cap B^{\prime}\right)$
1) 80
2) 100
3) 120
4) 140
Solution:
$ \begin{aligned} & \mathrm{n}(\mathrm{A} \cup \mathrm{B})=\mathrm{n}(\mathrm{A})+\mathrm{n}(\mathrm{B})-\mathrm{n}(\mathrm{A} \cap \mathrm{B}) \\ & =50+60-30=80 \\ & n\left(A^{\prime} \cap B^{\prime}\right)=n(A \cup B)^{\prime}=200-80=120 \end{aligned} $
Hence, the answer is 120.
Example 2: Given $n(A)=50, n(B)=30$ and $n(A U B)=x$ such that $n(A \cap B)=$20. Find $x$:
1) 20
2) 40
3) 60
4) 80
Solution:
We know,
$ \begin{aligned} & n(A \cup B)=n(A)+n(B)-n(A \cap B) \\ & x=50+30-20=60 \end{aligned} $
Hence, the answer is 60.
Example 3: The sum of integers from 1 to 100 that are divisible by 2 or 5 is
1) 3000
2) 3050
3) 3600
4) 3250
Solution:
Number of Elements in Union $A$ & $B$ -
$ \begin{aligned} & n(A \cup B)=n(A)+n(B)-n(A \cap B)\end{aligned} $
wherein
Given $A$ and $B$ are any finite sets. then the Number of Elements in union $A$ & $B$ is given by this formula.
$ \begin{aligned} & S=2+4+5+6 \\ & =(\text { sum of integers divisible by } 2)+(\text { sum of integers divisible by } 5)-(\text { sum of integers divisible by } 10(5 \times 2)) \\ & =(2+4+6+8 \ldots \ldots . .100)+(5+10+15 \ldots \ldots .100)-(10+20+\ldots \ldots \ldots+10) \\ & \text { sum of } n \text { term of an } A P \\ & =\frac{n}{2}(a+l) \\ & a=\text { first term } \\ & l=\text { last term } \\ & =\frac{50}{2}(2+100)+\frac{20}{2}(5+100)-\frac{10}{2}(10+100) \\ & =2550+1050-550=3050 \end{aligned} $
Hence, the answer is 3050.
Example 4: $ \text { If } A \cap B=\phi, n(A)=50, n(B)=70 \text {. Then evaluate } n(A \cup B) \text {. }$
1) 50
2) 70
3) 20
4) 120
Solution:
$\begin{equation} \begin{aligned} &\text { We know, }\\ &\begin{aligned} & n(A \cup B)=n(A)+n(B)-n(A \cap B) \\ & \text { Since } A \cap B=\phi, n(A \cap B)=0 \\ & n(A \cup B)=50+70-0=120 \end{aligned} \end{aligned} \end{equation}$
Hence, the answer is 120.
Solution:
Number of Elements in Union $A, B$ & $C$ -
$ \begin{aligned} & n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(A \cap C)-n(B \cap C)+n(A \\ & \cap B \cap C) \\\end{aligned} $
wherein
Given $\mathrm{A}, \mathrm{B}$, and C are any finite sets. then the Number of Elements in union $A$ , $B$ & $C$ is given by this formula.
From the concept,
Let $n(M)=$ no. of students opted maths $=70$
$n(P)=$ student opted physics $=40$
$\mathrm{n}(\mathrm{C})=$ student opted chemistry $=28$
$n(M \cap P)=$ number of students opted for physics and maths $=23$
$n(M \cap C)=$ number of students opted for maths and chemistry = 14
$n(P \cap C)=$ number of students opted for physics and chemistry $=9$
$n(M \cap P \cap C)=$ number of students opted for all three students $=4$
So the total number of students who opted for at least one subject $=$
$n(M \cup P \cup C)=n(M)+n(P)+n(C)-n(M \cap P)-n(M \cap C)-n(P \cap C)+n(M \cap P \cap C)$
So putting the values, we have
$n(M \cup P \cup C)=70+46+28-23-14-9+4=102$
Hence total no. of students who have not adopted any course $=$ total number of students -total number of students who opted for at least one course $=140-$ $102=38$
Hence, the answer is 38.
List of Topics Related to Cardinal Numbers of Some Sets
Understanding the cardinal number of sets becomes easier when you explore its related foundational concepts. From the roster and set-builder forms to universal sets, subsets, De Morgan’s laws, and more, each topic builds the groundwork for mastering set theory. In this section, we’ve listed all the essential topics linked to the cardinal numbers of some sets to help you revise key ideas and strengthen your conceptual clarity.
NCERT Resources
Strengthen your understanding of Class 11 Sets with high-quality NCERT study materials, designed to align with board exam patterns and competitive exam needs. These NCERT resources include detailed solutions, quick revision notes, and well-curated exemplar problems to support concept clarity and practice. Access all the key materials for NCERT Chapter 1 Sets below.
NCERT Solutions for Class 11 Chapter 1 Sets
Practice Questions on Cardinal Number of a Set
Consistent practice is key to mastering the concept of the cardinal number of a set in mathematics. These carefully designed practice questions will help you revise important formulas, understand core properties, and apply them in different contexts. Whether you're preparing for board exams or competitive tests, solving a cardinal number of set MCQs will boost your accuracy and confidence. Attempt the questions below and explore more practice topics from the Sets chapter.
To practice questions based on Cardinal Number Of Some Sets - Practice Question MCQ, click here.
You can practice some important topics of Sets below:
Frequently Asked Questions (FAQs)
6 is the cardinal number for any set containing 6 elements.
$n(A \cup B)=n(A)+n(B)-n(A \cap B)$
It helps in counting the total elements present in the set.
The number of distinct elements in a finite set $A$ is called the Cardinal number of $\operatorname{set} A$. Example: Let $A = \{s,m,t,d,r,h\}$, then $n(A) = 6$
The cardinal number of set A is 4.