De-Morgan's Laws

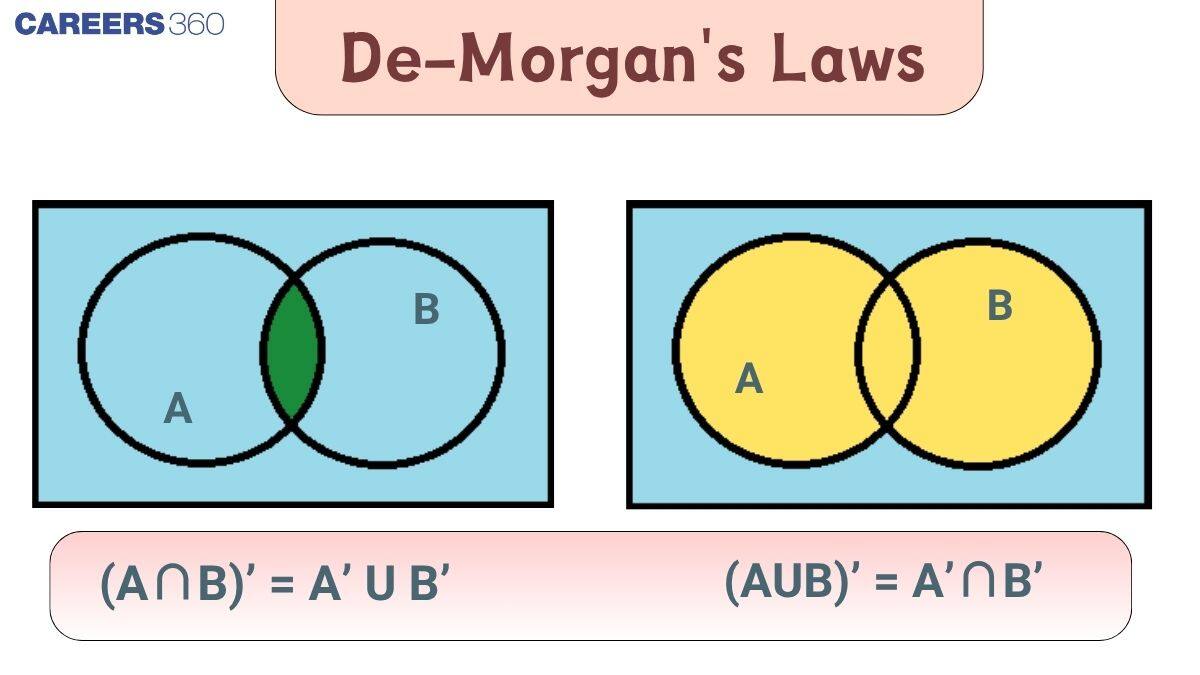
What are De-Morgan's Laws in Sets?

In set theory, the relationship between union, complements, and intersection is provided by De-Morgan's law. It provides the relationship between AND, OR, and the variable's complements in Boolean algebra; in logic, it provides the relationship between AND, OR, or the statement's negation. De Morgan's Law allows us to optimise different Boolean circuits that use logic gates to do the same task with a minimum amount of equipment.

According to De-Morgan's Laws:

• The complement of the union of two sets is equal to the intersection of their individual complements.
• Additionally, the complement of the intersection of two sets is equal to the union of their individual complements.

De-Morgan's Law of Sets Formula

De Morgan's Law Formula outlines two fundamental rules in set theory that connect the operations of union, intersection, and complement. These laws are essential for simplifying set expressions and solving problems in logic, Boolean algebra, and mathematics.

First De-Morgan's Law: Law of Union

The first law of De Morgan states that the complement of the union of two sets is equal to the intersection of their individual complements. This principle is widely applied in set theory problems, Venn diagrams, and logic gate circuits.

If $A$ and $B$ are two sets, then:

$(A \cup B)' = A' \cap B'$

Where:

• $\cup$ denotes the union of sets
• $\cap$ denotes the intersection of sets
• $'$ denotes the complement of a set

This is also known as De-Morgan's Law of Union.

Second De-Morgan's Law: Law of Intersection

The second law of De Morgan states that the complement of the intersection of two sets is equal to the union of their individual complements. This law helps in transforming and simplifying logical and mathematical statements involving negations.

If $A$ and $B$ are two sets, then:

$(A \cap B)' = A' \cup B'$

Where:

• $\cap$ denotes the intersection of sets
• $\cup$ denotes the union of sets
• $'$ denotes the complement of a set

This is also referred to as De-Morgan's Law of Intersection.

De-Morgan's Law Proof

De-Morgan’s Laws in set theory explain how the complement of unions and intersections of sets behaves under set operations. These laws help us simplify set expressions and are widely used in mathematics, logic, and computer science.

expressions and are widely used in mathematics, logic, and computer science.

Proof of De-Morgan’s Law of Union

De-Morgan’s Law of Union states:

$(A \cup B)' = A' \cap B'$

This means that the complement of the union of two sets $A$ and $B$ is equal to the intersection of their individual complements.

Let $x \in (A \cup B)'$
Then:

$x \in (A \cup B)' \Leftrightarrow x \notin (A \cup B)$

$\Leftrightarrow x \notin A \text{ and } x \notin B$

$\Leftrightarrow x \in A' \text{ and } x \in B'$

$\Leftrightarrow x \in (A' \cap B')$

$(A \cup B)' = A' \cap B'$

So, any element that does not belong to $A \cup B$ must belong to both $A'$ and $B'$, proving the sets are equal.

Generalised Form (for n sets):

$\left( \bigcup_{i=1}^n A_i \right)' = \bigcap_{i=1}^n A_i'$

This generalisation holds for any number of sets.

Proof of De-Morgan’s Law of Intersection

De-Morgan’s Law of Intersection states:

$(A \cap B)' = A' \cup B'$

This means that the complement of the intersection of two sets $A$ and $B$ is equal to the union of their individual complements.

Let $x \in (A \cap B)'$
Then:

$x \in (A \cap B)' \Leftrightarrow x \notin (A \cap B)$

$\Leftrightarrow x \notin A \text{ or } x \notin B$

$\Leftrightarrow x \in A' \text{ or } x \in B'$

$\Leftrightarrow x \in (A' \cup B')$

$(A \cap B)' = A' \cup B'$

Thus, any element that is not common to both sets $A$ and $B$ must be in at least one of their complements, proving the identity.

Generalised Form (for n sets):

$\left( \bigcap_{i=1}^n A_i \right)' = \bigcup_{i=1}^n A_i'$

These formal proofs confirm that De Morgan’s laws in set theory hold true and are useful for simplifying complex set expressions and logic operations.

De-Morgan's Law Truth Table

De-Morgan's Laws describe how complements interact with unions and intersections. These logical equivalences can be verified using truth tables.

De-Morgan's First Law Statement and Proof

Statement:
The complement of the union of two sets is equal to the intersection of their individual complements.

$(A \cup B)' = A' \cap B'$

Truth Table:

De-Morgan's Second Law Statement and Proof

Statement:
The complement of the intersection of two sets is equal to the union of their individual complements.

$(A \cap B)' = A' \cup B'$

Truth Table:

De-Morgan's Law Examples

Let us understand De-Morgan’s Laws using a simple example.

Let the universal set be:
$U = \{7, 8, 9, 10, 11, 12, 13\}$

Let the two subsets be:
$A = \{11, 12, 13\}$
$B = \{7, 8\}$

De-Morgan’s Law of Union example

We have: $A \cup B = \{7, 8, 11, 12, 13\}$
Therefore,
$(A \cup B)' = U - (A \cup B) = {9, 10}$

Also, $A' = U - A = \{7, 8, 9, 10\}$
$B' = U - B = \{9, 10, 11, 12, 13\}$
So, $A' \cap B' = \{9, 10\}$

Hence, $(A \cup B)' = A' \cap B'$

De-Morgan’s Law of Intersection example

We have:
$A \cap B = \phi$
So, $(A \cap B)' = U - \phi = U = {7, 8, 9, 10, 11, 12, 13}$

Also, $A' = {7, 8, 9, 10}$
$B' = {9, 10, 11, 12, 13}$
So, $A' \cup B' = {7, 8, 9, 10, 11, 12, 13}$

Thus, $(A \cap B)' = A' \cup B'$

De-Morgan's Law in Boolean Algebra

De-Morgan's Laws are fundamental rules in Boolean Algebra that express how logical operations interact with negation. These laws help simplify logic circuits and Boolean expressions.

The two key formulas are:

1. $\overline{A + B} = \bar{A} \cdot \bar{B}$
2. $\overline{A \cdot B} = \bar{A} + \bar{B}$

Proof of De-Morgan's Law in Boolean Algebra

Let’s look into the proof of both De-Morgan’s Laws using Boolean identities:

1. Proof of $\overline{A + B} = \bar{A} \cdot \bar{B}$

We start with: $\overline{A + B} = 1 - (A + B)$  (Using the complement property)
= $(1 - A) \cdot (1 - B)$  (Using distributive property of subtraction)

Now, by the definition of complement:
$(1 - A) = \bar{A}$ and $(1 - B) = \bar{B}$

Hence, $\overline{A + B} = \bar{A} \cdot \bar{B}$

2. Proof of $\overline{A \cdot B} = \bar{A} + \bar{B}$

We start with: $\overline{A \cdot B} = 1 - (A \cdot B)$  (Using the complement property)
= $(1 - A) + (1 - B)$  (Using distributive property of subtraction)

Again, using complement definitions:
$(1 - A) = \bar{A}$ and $(1 - B) = \bar{B}$

Thus, $\overline{A \cdot B} = \bar{A} + \bar{B}$

Solved Examples of De-Morgan's Law

Example 1: If $(A \cup B)=P$, then evaluate $P^{\prime}$
1) $A^{\prime} \cup B$
2) $A \cap B^{\prime}$
3) $A^{\prime} \cup B^{\prime}$
4) $A^{\prime} \cap B^{\prime}$

Solution:
Using De-Morgan's Law:
$P^{\prime}=(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}$
Hence, the answer is option 4.

Example 2: Which of the following is not a property of a union of sets?
1) $A \cup(B \cup C)=(A \cup B) \cup C$
2) $A \cup B=B \cup A$
3) $(A \cup B)^c=A^c \cup B^c$
4) $(A \cap B)^c=A^c \cup B^c$

Solution:
Let $A$ and $B$ be any two sets. The union of $A$ and $B$ is the set which consists of all the elements of $A$ and all the elements of $B$, the common elements being taken only once. The symbol ' $u$ ' is used to denote the union.

Symbolically, we write $A \cup B=\{x: x \in A$ or $x \in B\}$.
De Morgan's Law -
$(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}$
Hence, option 3 is incorrect.
Hence, the answer is option 3.

Example 3: If $(A \cap B \cap C)=P$. Then evaluate $P^{\prime}$
1) $A^{\prime} \cap B^{\prime} \cap C^{\prime}$
2) $A^{\prime} \cup B^{\prime} \cup C^{\prime}$
3) $A^{\prime} \cup B^{\prime} \cap C^{\prime}$
4) $A^{\prime} \cup B^{\prime} \cap C^{\prime}$

Solution:
$P' = (A \cap B \cap C)'$

$= ((A \cap B) \cap C)'$

$= (A \cap B)' \cup C' \quad \text{(by De Morgan's Law)}$

$= A' \cup B' \cup C'$

Hence, the answer is option 2.

Example 4: If the set $A^{\prime}=\{3,5,7\}$ and $B^{\prime}=\{1,5,9\}$, then the set $(A \cup B)^{\prime}=$
1) $\{1,3,5,7,9\}$
2) $\{5,7\}$
3) $\{5\}$
4) $\{1,5,9\}$

Solution:
De Morgan's Law:
$(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}$
The intersection of $\mathrm{A}^{\prime}$ and $\mathrm{B}^{\prime}$ is $\{5\}$.
Hence, the answer is option 3.

Example 5: If $A-B=X$ and $A-C=Y$. then the simplification of $A-(B \cup C)$ is
1) $X \cap Y$
2) $X \cup Y$
3) $X-Y$
4) $Y-X$

Solution:
$P-Q=P \cap Q^{\prime}$
So,
$A - (B \cup C) = A \cap (B \cup C)'$

$A \cap (B' \cap C') = (A \cap B') \cap (A \cap C') = (A - B) \cap (A - C)$

$X \cap Y$
Hence, the answer is option 1.

List of Topics Related to De-Morgan's Laws

To fully understand De-Morgan's Laws in set theory, it's important to first grasp the foundational set concepts they rely on. This section outlines key related topics like the roster and set-builder forms, types of sets, subsets, and operations such as difference and union. Mastery of these topics will help build the logical base needed to apply De-Morgan’s Laws accurately.

NCERT Resources

Access curated NCERT resources to strengthen your understanding of Sets. This section includes detailed solutions, revision notes, and exemplar problems from Class 11 Chapter 1, helping you build a strong foundation for exams through structured and NCERT-aligned preparation.

NCERT Solutions for Class 11 Chapter 1 Sets

NCERT Notes for Class 11 Chapter 1 Sets

NCERT Exemplar for Class 11 Chapter 1 Sets

Practice Questions on De-Morgan's Law in Sets

Sharpen your grasp of De-Morgan's Laws in Sets with targeted practice questions. This section offers a variety of MCQs designed to test your understanding of definitions, properties, and logical applications. You’ll also find practice sets on related foundational topics to strengthen your overall command of set theory.

To practice questions based on De Morgan's Laws - Practice Question MCQ, click here.

You can practice some important topics of Sets below: