Functions, Image and Pre-image: Definition and Examples
Functions, image, and pre-image are important concepts in mathematics that help us understand how values are related through a rule or mapping. In a function, the image refers to the output values, while the pre-image refers to the input values that lead to those outputs. Knowing the difference between image and pre-image is essential for topics like domain, range, and function mapping in both algebra and set theory. These ideas are not only useful in solving mathematics problems but also in understanding real-life situations involving relationships between quantities. In this article, we will explain the meaning of functions, image, and pre-image with definitions, examples, diagrams, and practice problems.
This Story also Contains
- Introduction to Functions, Image, and Pre-image
- Image of a Function
- Pre-image of a Function
- Image vs Pre-image in Functions
- Solved Examples Based On the Image and Pre-image of Functions
- List of Topics related to Functions, Image and Pre-Image
- NCERT Resources
- Practice Questions based on Functions, Image and Pre-Image
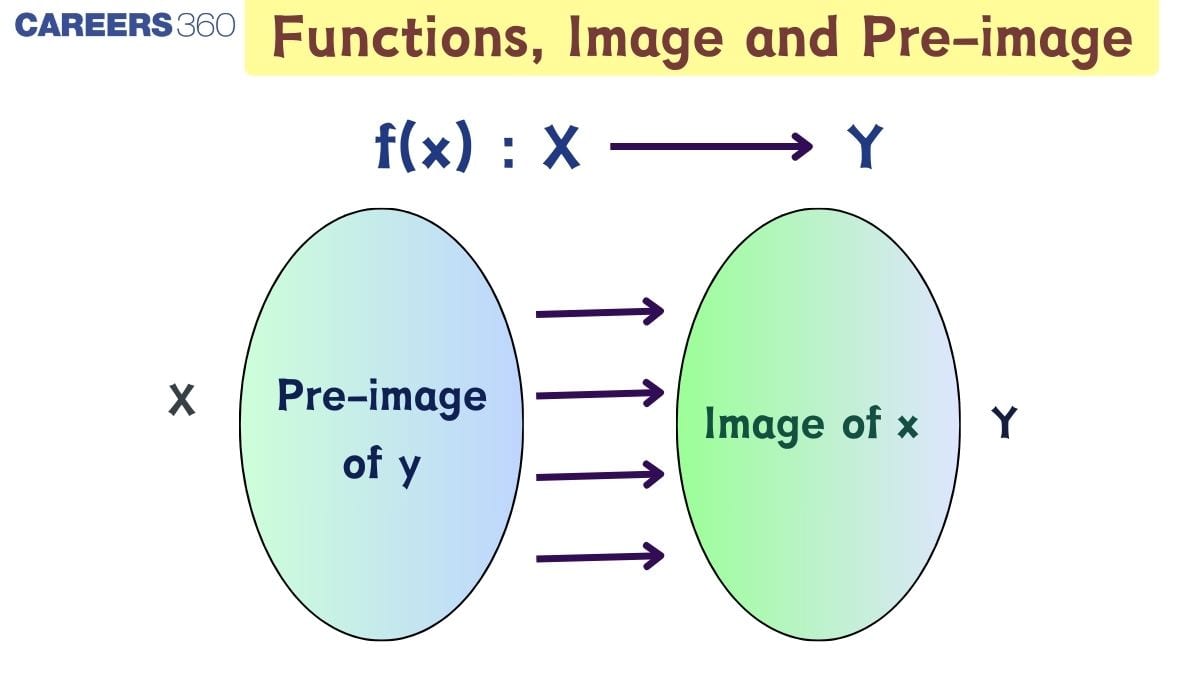
Introduction to Functions, Image, and Pre-image
Functions, image, and pre-image are fundamental ideas in mathematics that describe how inputs are connected to outputs. The image of a function is the set of resulting values after applying the function rule, while the pre-image is the set of original inputs that produce a given output. These concepts are essential for understanding domain, range, and mapping in algebra and set theory.
What is a Function in Mathematics?
A function is a special type of relation where every element of the input set (domain) is paired with exactly one element of the output set (codomain).
Definition:
A relation from a set $A$ to a set $B$ is said to be a function from $A$ to $B$ if every element of set $A$ has one and only one image in set $B$.
Alternate form:
If $A$ and $B$ are two non-empty sets, then a relation from $A$ to $B$ is said to be a function if each element $x$ in $A$ is assigned a unique element $f(x)$ in $B$, and it is written as:
$f: A \rightarrow B$
This is read as "$f$ is a mapping from $A$ to $B$".
Example:
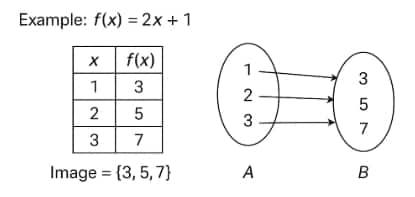
If $f(x) = 2x + 1$ and $A = {1, 2, 3}$, then the mapping is:
$f(1) = 3,\ f(2) = 5,\ f(3) = 7$
Understanding Domain, Range, and Mapping
Domain: The set of all possible input values (pre-images). For $f(x) = x^2$, the domain can be all real numbers $\mathbb{R}$.
Range: The set of all possible output values (images). For $f(x) = x^2$, the range is $[0, \infty)$.
Mapping: The pairing between each domain element and its range element. This can be shown with an arrow diagram:
$1 \rightarrow 3,\ 2 \rightarrow 5,\ 3 \rightarrow 7$
Mapping diagrams make it clear how pre-images from the domain lead to images in the range.
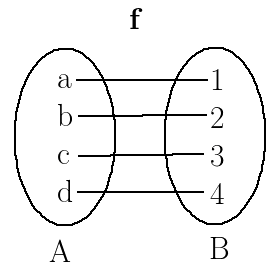
Function
Function
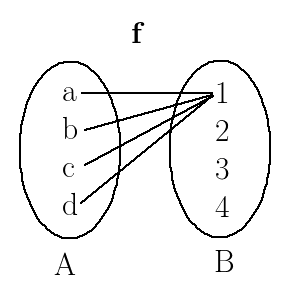
Not a function
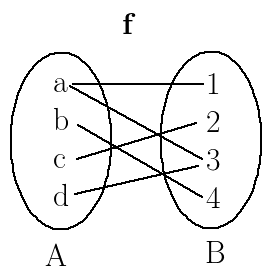
Not a function
The third one is not a function because $d$ is not related(mapped) to any element in $B$.
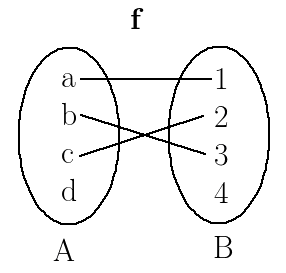
Fourth is not a function as element a in $A$ is mapped to more than one element in $B$.
Image of a Function
The image of a function refers to the set of all output values that the function produces from its domain.
Definition:
Given a function $f: A \rightarrow B$ and a subset $X \subseteq A$, the image of $X$ under $f$ is:
$f(X) = \{ f(x) \mid x \in X \}$
If we take the entire domain $A$, the image of the function $f$ (also called the range) is:
$\text{Image}(f) = f(A) = \{ f(a) \mid a \in A \}$
Important Notes:
Always specify whether you are talking about the image of an element or of a subset.
$f(x)$ is an element of the codomain, whereas $f(C)$ is a subset of the codomain.
If $y \in f(C)$, then $y \in B$ and there exists an $x \in C$ such that $f(x) = y$.
How to Find the Image of a Function
Start with the function rule $f(x)$.
Substitute each input from the domain into $f(x)$.
Collect all distinct outputs — these form the image.
Example: For $f(x) = 2x + 1$ and $A = {1, 2, 3}$, the image is:
$f(1) = 3,\ f(2) = 5,\ f(3) = 7$
So, $\text{Image}(f) = {3, 5, 7}$.
Example : If $f(x) = x^2$ and $A = {-2, -1, 0, 1, 2}$,
$f(-2) = 4,\ f(-1) = 1,\ f(0) = 0,\ f(1) = 1,\ f(2) = 4$
Thus, $\text{Image}(f) = {0, 1, 4}$.
Image in Set Theory and Real-Life Applications
Set Theory: Images are used to define mappings and to check properties like injectivity and surjectivity.
Real-Life: For example, if a function converts Celsius to Fahrenheit, the set of temperatures in Fahrenheit you get is the image of the Celsius inputs.
Pre-image of a Function
The pre-image of a function is the set of all input values that map to a specific output value or set of output values.
Definition:
Given a function $f: A \rightarrow B$ and a subset $Y \subseteq B$, the pre-image of $Y$ under $f$ is:
$f^{-1}(Y) = \{ x \in A \mid f(x) \in Y \}$
If $y \in B$, the pre-image of ${y}$ is:
$f^{-1}(\{y\}) = \{ x \in A \mid f(x) = y \}$
Steps to Find the Pre-image of a Function
Identify the output value(s) in $B$.
Solve the equation $f(x) = y$ for $x$.
Collect all solutions — these form the pre-image.
Example: If $f(x) = x^2$ and $y = 4$,
$x^2 = 4 \quad \Rightarrow \quad x = -2,\ 2$
So, $f^{-1}({4}) = {-2, 2}$.
Pre-image of a Set Under a Function
If $Y = {1, 4}$ and $f(x) = x^2$, then:
$f^{-1}(Y) = \{ x \in \mathbb{R} \mid x^2 = 1 \ \text{or} \ x^2 = 4 \}$
Thus, $f^{-1}(Y) = {-2, -1, 1, 2}$.
Pre-image Examples in Algebra and Set Theory
Algebra: In $f(x) = 3x - 1$, the pre-image of $5$ is found by solving $3x - 1 = 5 \ \Rightarrow \ x = 2$.
Set Theory: If $B = {b_1, b_2}$ and $f$ maps multiple $a_i$ to the same $b_j$, then all those $a_i$ are part of the pre-image of ${b_j}$.
Image vs Pre-image in Functions
In mathematics, image and pre-image describe the two sides of a function’s mapping process. The image focuses on the output side (results), while the pre-image focuses on the input side (origins). Understanding both helps in analysing the domain, range, and the overall behaviour of a function.
Difference Between Image and Pre-image
Aspect | Image | Pre-image |
Definition | The set of all output values produced by a function. | The set of all input values that map to a given output or set of outputs. |
Notation | $f(X) = {f(x) \mid x \in X}$ | $f^{-1}(Y) = {x \in A \mid f(x) \in Y}$ |
Set Location | Subset of the codomain | Subset of the domain |
Focus | Output side of mapping | Input side of mapping |
Example | If $f(x) = 2x$, the image of ${1, 3}$ is ${2, 6}$. | For $f(x) = 2x$, the pre-image of ${4, 8}$ is ${2, 4}$. |
Relation Between Image, Pre-image, Domain, and Range
Domain ($A$) – The set of all possible input values. Every pre-image belongs to the domain.
Range (Image of Entire Domain) – The set $f(A)$ consisting of all actual outputs of $f$.
Image of a Subset ($f(X)$) – Outputs corresponding to inputs in subset $X \subseteq A$.
Pre-image of a Subset ($f^{-1}(Y)$) – Inputs that produce outputs in subset $Y \subseteq B$.
Key Relation:
If $y \in f(X)$, then $\exists, x \in X$ such that $f(x) = y$.
If $x \in f^{-1}(Y)$, then $f(x) \in Y$.
Example:
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be $f(x) = x^2$.
Domain: $\mathbb{R}$
Range: $[0, \infty)$
Image of ${-2, 2, 3}$: ${4, 9}$
Pre-image of ${4, 9}$: ${-2, 2, -3, 3}$
Solved Examples Based On the Image and Pre-image of Functions
Example 1: A real-valued function $f(x)$ satisfies the functional equation
$f(x-y) = f(x) f(y) - f(a-x) f(a+y)$ where $a$ is a given constant and $f(0) = 1$.
1) $f(x)$
2) $-f(x)$
3) $f(-x)$
4) $f(a) + f(a-x)$
Solution:
$f(x-y) = f(x) f(y) - f(a-x) f(a+y)$
$f(0) = 1,\quad f(2a-x) = ?$
Put $x = 0,\ y = 0$:
$f(0) = f(0) \times f(0) - f(a) \times f(a)$
$1 = 1 - f^2(a)$
$f^2(a) = 0$
$f(a) = 0$
Now, $f(2a - x) = f(a + a - x) = f(a - (x-a))$
Let $x \rightarrow a$ and $y \rightarrow x-a$:
$f(a) f(x-a) - f(a-a) f(a + x-a) = 0 - 1 \times f(x) = -f(x)$
Hence, the answer is option 2.
Example 2: If $f(x) + 2f\left(\frac{1}{x}\right) = 3x,\ x \neq 0$, and
$S = \{x \in \mathbb{R} : f(x) = f(-x)\}$, then $S$:
1) is an empty set
2) contains exactly one element
3) contains exactly two elements
4) contains more than two elements
Solution:
$f(x) + 2f\left(\frac{1}{x}\right) = 3x$
Interchanging $x$ with $\frac{1}{x}$:
$f\left(\frac{1}{x}\right) + 2f(x) = \frac{3}{x}$
Multiply the first equation by $2$:
$2f(x) + 4f\left(\frac{1}{x}\right) = 6x$
Compare with the second equation:
$2f\left(\frac{1}{x}\right) + f(x) = 3x$
Subtract:
$3f(x) = \frac{6}{x} - 3x$
$f(x) = \frac{2}{x} - x$
Now, $f(-x) = \frac{2}{-x} + x$
Set $f(x) = f(-x)$:
$\frac{2}{x} - x = -\frac{2}{x} + x$
$\frac{4}{x} - 2x = 0$
$\frac{4 - 2x^2}{x} = 0$
$4 = 2x^2$
$x^2 = 2$
$x = \pm\sqrt{2}$, $x \neq 0$
Hence, the answer is option 3.
Example 3: Which of the following relations is not a function?
1) $\{(1,2), (1,3), (2,3), (1,4)\}$
2) $\{(1,2), (2,2), (3,2), (5,4)\}$
3) $\{(1,2), (3,4), (5,6)\}$
4) $\{(1,2), (3,4)\}$
Solution:
In option 1, the element $1$ has two images, $2$ and $3$. Hence it is not a function.
Hence, the answer is option 1.
Example 4: If $n(A) = 4$ and $n(B) = 3$, then the total number of functions from $A$ to $B$ is:
Solution:
As we learned, the number of functions:
$f: A \rightarrow B$
$n(A) = m$
$n(B) = n$
Total number of functions $= n^m$
Number of functions $= (n(B))^{n(A)}$
$= 3^4 = 81$
Hence, the answer is $81$.
Solution:
As we learned, the number of functions:
$f: A \rightarrow B$
$n(A) = m$
$n(B) = n$
Total number of functions $= n^m$
Since $3125 = 5^5$
Thus, $n(A) = n(B) = 5$
Thus, $n(A) + n(B) = 10$
Hence, the answer is $10$.
List of Topics related to Functions, Image and Pre-Image
Understanding functions, image, and pre-image opens the door to many important topics in mathematics. From algebraic functions to domain, co-domain, and range, each concept helps us explore how inputs map to outputs. Learning about piecewise functions, transformations of functions, and the Cartesian product with ordered pairs gives a complete picture of how relationships between sets work. These topics build a strong foundation for solving problems in algebra, set theory, and beyond.
NCERT Resources
For mastering functions, image, and pre-image, NCERT resources offer clear explanations and practice. The NCERT notes for Class 12 Maths Chapter 1: Relations and Functions give a quick revision of key concepts, while the NCERT solutions help in step-by-step problem solving. The NCERT exemplar solutions go deeper with advanced questions, strengthening understanding and application skills.
NCERT Notes for Class 12 Maths Chapter 1 - Relations and Functions
NCERT Solutions for Class 12 Maths Chapter 1 - Relations and Functions
NCERT Exemplar Solutions for Class 12 Maths Chapter 1 - Relations and Functions
Practice Questions based on Functions, Image and Pre-Image
Strengthen your understanding of functions, image, and pre-image with targeted practice questions and MCQs. Test your knowledge on important topics like domain, co-domain, and range of a function, one-to-one and many-to-one functions, onto and into functions, and bijective functions. You can also practice composition of functions, their conditions and properties, as well as finding the inverse of a function. These questions are designed to improve both conceptual clarity and problem-solving speed.
Functions Image And Pre Image Practice Question MCQ
You can practice the following topics:
Frequently Asked Questions (FAQs)
The number of functions-
Total number of functions =nm
The number of functions =$2^3=8$
The pre-image of a function refers to the set of all input values that produce a given output value or set of output values.
If any line drawn parallel to the y-axis cuts the curve at most one point, then it is a function.
If any such line cuts the graph at more than one point, then it is not a function.
A relation from a set A to a set B is said to be a function from A to B if every element of set A has one and only one image in set B.
The image of a function refers to the set of all output values it produces from its domain.