Many One Function - Definition, Formula and Examples
A many-one function, in mathematics is also known as a surjective function, is a function where each domain element is mapped to one or more elements in the codomain. In other words, two different elements in the domain map to the same element in the codomain. The deep knowledge of many-one functions is fundamental in various branches of mathematics, particularly in algebra and calculus.
This Story also Contains
- What is many-one function?
- Examples of many one function
- Graph of Many to One Function
- Properies of many-one funcion
- One one and Many one function
- Solved Examples Based on Many One Function
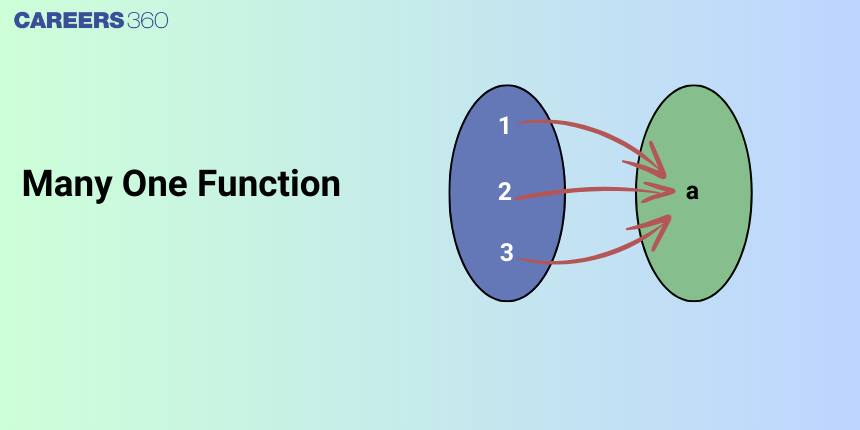
In this article, we will cover the concept of many-one functions. This concept falls under the broader category of relation and function. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of one question have been asked on this concept, including one in 2023.
What is many-one function?
A function $f: X \rightarrow Y$ is called a many-one function if two or more elements of set $X$ have the same image in set $Y$,
Or we can say that if $f: X \rightarrow Y$ is many- one if it is not one-one function.
We can also check this property of the function with the help of a graph. If we plot the graph of corresponding $x$ and $y$ values, we will observe that $A$ line parallel to the x-axis cuts the curve at more than one point. This proves that the function is many one in nature.

Both the functions are many one, as in both there are two elements $x_2, x_3$ which corresponds to the same image $y_3$, i.e. $f\left(x_2\right)=f\left(x_3\right)=y_3$
We may define Many one function as a function in which two or more elements of a set are connected to a single element of another set. The function $f: x → y$, such that two or more elements in the domain of the function $f$ and belonging to the set $x$ are connected to a single element in the codomain of the function $f$ and belonging to the set $y$.
Let us consider an example with two sets with the set $\mathrm{P}=$ $\{6,7,8,9,10\}$ as the domain, and the Set $B=\{A, B, C\}$ as the range. Here the function $f$ from $A$ to $B$ is said to be many one function, if we have $\mathrm{f}=\{(6, \mathrm{~A}),(7, \mathrm{~A}),(8, \mathrm{~A}),(9, \mathrm{~B}),(10, \mathrm{C})\}$.
The many one functions can also be called a constant function if all the elements of the domain are connected to only one element in the codomain. And the many one function is called an onto function if each element in the range has been utilized.
Examples of many one function
We define the domain,codomain of some important many one functions:
Square function:
- Domain: All real numbers $(R)$
- Codomain: Non-negative real numbers ([0, $\infty)$ )
- Function: $f(x)=x^2$
Absolute value function
- Domain: All real numbers $(R)$
- Codomain: Non-negative real numbers ([0, =))
- Function: $f(x)=|x|$
Floor function:
- Domain: All real numbers $(R)$
- Codomain: All Integers $(Z)$
- Function: $f(x)=\lceil x\rceil$
Graph of Many to One Function
The important conclusion here is that the graph of a many-to-one function doesn’t pass the horizontal line test for at least one point in its range. The method to test whether a function is many one or not is as follows:
To check whether a function is many-one, we have to draw a line parallel to the x-axis on the graph. If it intersects the graph at more than one point, the function is a many-one function.
Let's consider an example of a many-one function, i.e., $f(x)=x^2$. As $x^2$ maps both $1$ and $-1$ to $1$, it is an example of a many-to-one function.

Properies of many-one funcion
The following is a list of some important properties of Many-One Function:
- The condition for constant function is that if there is just one codomain.
- There should always be more elements in the domain of many one functions as compared to that of the codomain.
- There cannot exist an inverse function for a many-to-one function.
- At least two components in the function's domain should share the same codomain value.
- A single output may comeout from more than one inputs. Distinct inputs (Domains) may give identical results.
- The many-to-one function is also known as the onto function if each value in the range has an input image.
One one and Many one function
| Feature | One-to-One Function (Injection) | Many-to-One Function |
|---|---|---|
| Definition | Each element in the domain maps to a unique element in the codomain. | At least two distinct elements in the domain map to the same element in the codomain. |
| Relationship between inputs and outputs | Precise one-to-one correspondence. No two inputs produce the same output. | Multiple inputs can produce the same output. |
| Horizontal Line Test | No horizontal line intersects the graph more than once. | A horizontal line can intersect the graph multiple times. |
| Example | $f(x)=x, f(x)=x^3$, etc. | (x)=x^2, f(x)=\sin (x) \text {, etc. } |
Recommended Video Based on Many one Function
Solved Examples Based on Many One Function
Example 1: Find the domain and range of the many one function $f=\{(4, x),(5, x),(6, x),(7, y),(8, y),(9, z)\}$
Solution:
The given function is $f=\{(4, x),(5, x),(6, x),(7, y),(8, y),(9, z)\}$
Here we have:
Domain $=(4,5,6,7,8,9)$
Range $=(x, y, z)$
We observe that the elements $4, 5,$ and $6$ in the domain are all connected to the same element '$x$' in the range. Hence, this function, which connects multiple elements in the domain to a single element in the range, is a many-one function.
Therefore, the given function is a many-one function.
Example 2: Which of the following is a many-one function?
1) $f(x)=\log (x)$
2) $f(x)=2^x$
3) $f(x)=x^{10}$
4) None of these
Solution:
Graphs of the functions given in the options are
1) $y=\log (x)$

Clearly, one-one
2) $y=2^x$

Clearly. one-one
3) $y=x^{10}$

Many-one
Alternatively, this is a polynomial of even degree, so many-one
So, $\mathrm{f}(\mathrm{x})=x^{10}$ is a many-one function.
Hence, the answer is option 3.
Example 3: Which of the following functions is a many-one function?
1)

2)

3)

4) None of these
Solution:
For second option

we can have many horizontal lines that cut the graph at more than one point. So it is many one function.
Example 4: Show that the function $f: R \rightarrow R$ defined by $f(x)=3 x^2+5, \forall x \in R$ is many one function.
Solution: Since $f(-1)=3 \times(-1)^2+5=8$ and $f(1)=3 \times(1)^2+5=8$, so the different elements $-1$ and $1$ of the domain set $\mathrm{R}$ have the same image in the codomain set $\mathrm{R}$.
Therefore, $f$ is a many-one function. Hence proved.
Frequently Asked Questions (FAQs)
To check whether the graph is a one-to-one or many-to-one function, we will have to draw a line parallel to the X-axis. If it intersects with the graph at more than one point then it is known to be a many-to-one function.
The domain of many one function is the set of elements from the domain set, which have been connected to two or more elements of the codomain set.
The horizontal line test can be used to determine if a function is many-one.
Onto function: Every element in the codomain is the image of at least one element from the domain.
Many-one function: Multiple elements in the domain can map to the same element in the codomain, and not every element in the codomain is necessarily covered.