Vector Triple Product

Vector Triple Product: Definition

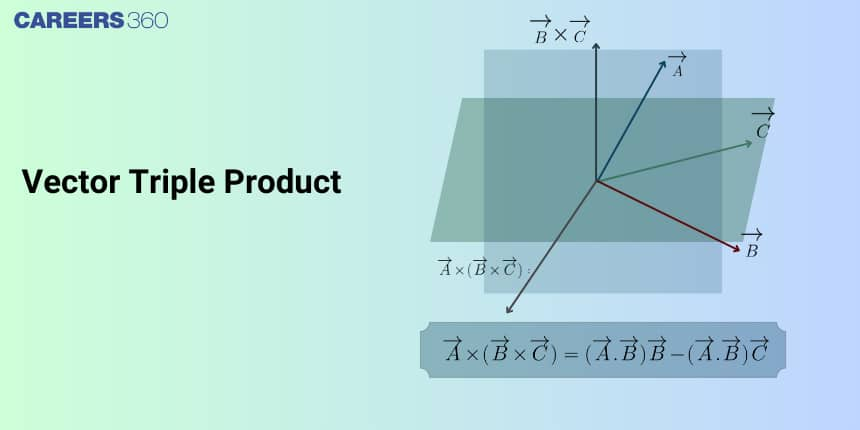
The Vector Triple Product is defined as the cross product of one of the vectors with the cross product of the other two vectors. It results in the vector. It is expressed as $\overrightarrow{\mathbf{a}} \times(\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}})$
The resultant of the triple cross vector lies in the plane of the given three vectors.
Formula of Vector Triple Product
For three vectors $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}}$ and $\overrightarrow{\mathbf{c}}$ vector triple product is defined as $\overrightarrow{\mathbf{a}} \times(\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}})$.

$
\vec{a} \times(\vec{b} \times \vec{c})=(\vec{a} \cdot \vec{c}) \cdot \vec{b}-(\vec{a} \cdot \vec{b}) \cdot \vec{c}
$

Derivation of Vector Triple Product

$\vec{p}=\vec{a} \times(\vec{b} \times \vec{c})$ is a vector perpendicular to $\vec{a}$ and $\vec{b} \times \vec{c}$ but $\vec{b} \times \vec{c}$ is a vector perpendicular to the plane of $\vec{b}$ and $\vec{c}$.
Hence, vector $\vec{p}$ must lie in the plane of $\vec{b}$ and $\vec{c}$.
Let $\vec{p}=\vec{a} \times(\vec{b} \times \vec{c})=l \vec{b}+m \vec{c}$
[l,m are scalars]
Taking the dot product of eq (i) with $\vec{a}$, we get

$
\begin{gathered}
\vec{p} \cdot \vec{a}=l(\vec{a} \cdot \vec{b})+m(\vec{a} \cdot \vec{c}) \\
{\left[\begin{array}{l}
\because \vec{a} \times(\vec{b} \times \vec{c}) \text { is } \perp \vec{a} \\
\therefore \vec{a} \times(\vec{b} \times \vec{c}) \cdot \vec{a}=0
\end{array}\right]}
\end{gathered}
$
Therefore,

$
\begin{array}{ll}
\Rightarrow & \vec{p} \cdot \vec{a}=0 \\
\Rightarrow & l(\vec{a} \cdot \vec{b})=-m(\vec{a} \cdot \vec{c}) \\
\Rightarrow & \frac{1}{\vec{a} \cdot \vec{c}}=\frac{-m}{\vec{a} \cdot \vec{b}}=\lambda \\
\Rightarrow & l=\lambda(\vec{a} \cdot \vec{c}) \\
\text { and } & m=-\lambda(\vec{a} \cdot \vec{b})
\end{array}
$

Substituting the value of $l$ and $m$ in Eq . (i), we get

$
\vec{a} \times(\vec{b} \times \vec{c})=\lambda[(\vec{a} \cdot \vec{c}) \vec{b}-(\vec{a} \cdot \vec{b}) \vec{c}]
$
Here, the value of $\lambda$ can be determined by taking specific values of $\vec{a}, \vec{b}$ and $\vec{c}$.

The simplest way to determine $\lambda$ is by taking specific vectors $\vec{a}=\hat{i}, \vec{b}=\hat{i}, \vec{c}=\hat{j}$.

We have,
$
\begin{array}{ll}
& \vec{a} \times(\vec{b} \times \vec{c})=\lambda[(\vec{a} \cdot \vec{c}) \vec{b}-(\vec{a} \cdot \vec{b}) \vec{c}] \\
& \hat{i} \times(\hat{i} \times \hat{j})=\lambda[(\hat{i} \cdot \hat{j}) \hat{i}-(\hat{i} \cdot \hat{i}) \hat{j}] \\
& \hat{i} \times \hat{k}=\lambda[(0) \hat{i}-(1) \hat{j}] \Rightarrow-\hat{j}=-\lambda \hat{j} \\
\therefore \quad & \lambda=1
\end{array}
$
Hence,

$
\vec{a} \times(\vec{b} \times \vec{c})=(\vec{a} \cdot \vec{c}) \vec{b}-(\vec{a} \cdot \vec{b}) \vec{c}
$

1.

$
\begin{aligned}
& \vec{a} \times(\vec{b} \times \vec{c})=(\vec{a} \cdot \vec{c}) \cdot \vec{b}-(\vec{a} \cdot \vec{b}) \cdot \vec{c} \\
& (\vec{a} \times \vec{b}) \times \vec{c}=(\vec{c} \cdot \vec{a}) \cdot \vec{b}-(\vec{c} \cdot \vec{b}) \cdot \vec{a}
\end{aligned}
$

2. In general $\vec{a} \times(\vec{b} \times \vec{c}) \neq(\vec{a} \times \vec{b}) \times \vec{c}$
If $\overrightarrow{\mathbf{a}} \times(\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}})=(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \times \overrightarrow{\mathbf{c}}$ then the vectors $\vec{a}$ and $\vec{c}$

NOTE: are collinear.

Properties of the Vector Triple Product
The vector triple product is a vector quantity.

$
\begin{aligned}
& \vec{a} \times(\vec{b} \times \vec{c}) \neq(\vec{a} \times \vec{b}) \vec{c} \\
& \vec{a} \times(\vec{b} \times \vec{c}) \text { is a vector perpendicular to } \vec{a} \text { and }(\vec{b} \times \vec{c})
\end{aligned}
$

$\vec{a} \times(\vec{b} \times \vec{c})$ is a vector perpendicular to the plane containing $\vec{a}, \vec{b}, \vec{c}$ are three vectors.

Recommended Video Based on Vector Triple Product

Solved Examples Based on Vector Triple Product

Example 1: If $\vec{a}, \vec{b}, \vec{c}$ are three non-zero vectors and $\hat{n}$ is a unit vector perpendicular to $\hat{c}$ such that $\vec{a}=\alpha \vec{b}-\hat{n}(a \neq 0)$ and $\vec{b} \cdot \vec{c}=12$, then $|\vec{c} \times(\vec{a} \times \vec{b})|_{\text {is equal to: }}$
[JEE MAINS 2023]
Solution

$
\begin{aligned}
& \overrightarrow{\mathrm{a}}=\alpha \overrightarrow{\mathrm{b}}-\hat{\mathrm{n}}, \vec{b} \cdot \overrightarrow{\mathrm{c}}=12 \\
& \overrightarrow{\mathrm{c}} \times(\vec{a} \times \vec{b})=(\vec{c} \cdot \vec{b}) \vec{a}-(\vec{c} \cdot \vec{a}) \vec{b} \\
& \overrightarrow{\mathrm{c}} \times(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}})=12 \vec{a}-(\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{b}}) \\
& \because \overrightarrow{\mathrm{a}}=\alpha \overrightarrow{\mathrm{b}}-\mathrm{n}
\end{aligned}
$
$
\vec{c} \cdot \vec{a}=\alpha \overrightarrow{\mathrm{c}} \cdot \vec{b}-\vec{c} \cdot \mathrm{n}
$
$
\vec{c} \cdot \vec{a}=12 \alpha
$
$
\begin{aligned}
& \vec{c} \times(\vec{a} \times \vec{b})=12 \vec{a}-12 \alpha \vec{b} \\
& |\vec{c} \times(\vec{a} \times \vec{b})|=12|\vec{a}-\alpha \vec{b}| \quad[\because \vec{a}-\alpha \vec{b}=-n \text { then }|\vec{a}-\alpha \vec{b}|=1] \\
& \Rightarrow|\vec{c} \times(\vec{a} \times \vec{b})|=12
\end{aligned}
$
$
|\overrightarrow{\mathrm{c}} \times(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}})|=12
$
Hence, the answer is 12

Example 2: Let $\lambda \in \mathbb{R}, \vec{a}=\lambda \hat{\imath}+2 \hat{\jmath}-3 \hat{k}, \vec{b}=\hat{\imath}-\lambda \hat{\jmath}+2 \hat{k}{ }_{\operatorname{If}}((\vec{a}+\vec{b}) \times(\vec{a} \times \vec{b})) \times(\vec{a}-\vec{b})=8 \hat{\imath}-40 \hat{\jmath}-24 \hat{k}$, then $|\lambda(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})|^2$ is equal to
Solution

$
\begin{aligned}
& ((\vec{a}+\vec{b}) \times(\vec{a} \times \vec{b}) \times(\vec{a}-\vec{b})-=8 \hat{i}-40 \hat{j}-24 \hat{k} \\
& \Rightarrow(\vec{a} \times(\vec{a} \times \vec{b})+\vec{b} \times(\vec{a} \times \vec{b})) \times(\vec{a}-\vec{b}) \\
& \Rightarrow((\vec{a} \cdot \vec{b}) \vec{a}-(\vec{a} \cdot \vec{a}) \vec{b}+(\vec{b} \cdot \vec{b}) \vec{a}-(\vec{b} \cdot \vec{a}) \vec{b}) \times(\vec{a}-\vec{b}) \\
& \Rightarrow 0-(\vec{a} \cdot \vec{b})(\vec{a} \times \vec{b})-a^2(\vec{b} \times \vec{a})+0-\mathrm{b}^2(\vec{a} \times \vec{b})-(\vec{a} \cdot \vec{b}) \vec{b} \times \vec{a}=8 \hat{\mathrm{i}}-40 \hat{\mathrm{j}}-24 \hat{\mathrm{k}} \\
& \Rightarrow\left(\mathrm{a}^2-\mathrm{b}^2\right)(\vec{a} \times \overrightarrow{\mathrm{b}})=8 \hat{\mathrm{i}}-40 \hat{\mathrm{j}}-24 \hat{\mathrm{k}} \\
& \left(\left(\lambda^2+4+9\right)-\left(1+\lambda^2+4\right)\right)(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) \\
& 8(\vec{a} \times \vec{b})=8(\hat{\mathrm{i}}-5 \hat{j}-3 \hat{k}) \\
& \hat{\mathrm{i}}(4-3 \lambda)-\hat{\mathrm{j}}(2 \lambda+3)+\hat{\mathrm{k}}\left(-\lambda^2-2\right)=\hat{\mathrm{i}}-5 \hat{\mathrm{j}}-3 \hat{\mathrm{k}} \\
& \Rightarrow 4-3 \lambda=1 \quad 2 \lambda+3=5 \quad-\lambda^2-2=-3 \\
& 3 \lambda=3 \\
& \lambda=1 \\
& \lambda \\
& \begin{array}{l}
\lambda^2=1
\end{array} \\
& \begin{array}{ll}
\lambda(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})|=|(\vec{a}+\vec{b}) \times\left.(\vec{a}-\vec{b})\right|^2 \\
\Rightarrow|-\vec{a} \times \vec{b}+\vec{b} \times \vec{a}|^2=|2(\vec{a} \times \vec{b})|^2=4(1+25+9)=140
\end{array}
\end{aligned}
$
Hence, the answer is 140

Example 3: Let $\vec{a}, \vec{b}$ and $\vec{c}$ be three non-zero vectors such that $\vec{b} \cdot \vec{c}=0$ and $\vec{a} \times(\vec{b} \times \vec{c})=\frac{b-\vec{c}}{2}$. If $\vec{d}$ be a vector such that $\vec{b} \cdot \vec{d}=\vec{a} \cdot \vec{b}$, then $(\vec{a} \times \vec{b}) \cdot(\vec{c} \times \vec{d})_{\text {is equal to }}$.
[JEE MAINS 2023]

$
\begin{aligned}
& \text { Solution: }(\overline{\mathrm{a}} \cdot \overline{\mathrm{c}}) \overline{\mathrm{b}}-(\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}) \overline{\mathrm{c}}=\frac{\overline{\mathrm{b}}}{2}-\frac{\overline{\mathrm{c}}}{2} \\
& \overline{\mathrm{a}} \cdot \overline{\mathrm{c}}=\frac{1}{2}, \overline{\mathrm{a}} \cdot \overline{\mathrm{b}}=\frac{1}{2} \\
& \overline{\mathrm{b}} \cdot \overline{\mathrm{d}}=\frac{1}{2} \\
& (\overline{\mathrm{a}} \times \overline{\mathrm{b}}) \cdot(\overline{\mathrm{c}} \times \overline{\mathrm{d}})=\overline{\mathrm{a}} \cdot[\overline{\mathrm{b}} \times(\overline{\mathrm{c}} \times \overline{\mathrm{d}})] \\
& =\overline{\mathrm{a}} \cdot[(\overline{\mathrm{b}} \cdot \overline{\mathrm{d}}) \overline{\mathrm{c}}-(\overline{\mathrm{b}} \cdot \overline{\mathrm{c}}) \overline{\mathrm{d}}] \\
& =\overline{\mathrm{a}} \cdot[\overline{\mathrm{c}} / 2] \\
& =\frac{1}{2}(\overline{\mathrm{a}} \cdot \overline{\mathrm{c}}) \\
& =\frac{1}{4}
\end{aligned}
$
Hence, the answer is $1 / 4$

Example 4: Let $\vec{a}, \vec{b}, \vec{c}$ be three vectors mutually perpendicular to each other and have the same magnitude. If a vector $\vec{r}$ satisfies $\vec{a} \times\{(\vec{r}-b) \times \vec{a}\}+b \times\{(\vec{r}-\vec{c}) \times b\}+\vec{c} \times\{(\vec{r}-\vec{a}) \times \vec{c}\}=0$,then $\vec{r}$ is equal to:
Solution: $|\vec{a}|=|\vec{b}|=|\vec{c}|$ and $\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{c}=\vec{c} \cdot \vec{a}=0$
Let $\vec{r}=x \vec{a}+y \vec{b}+z \vec{c}$
where $\vec{r} \cdot \vec{a}=x|\vec{a}|^2, \vec{r} \cdot \vec{b}=y|\vec{b}|^2, \vec{r} \cdot \vec{c}=z|\vec{c}|^2$
Give expression is

$
\begin{aligned}
& (\vec{a} \times(\vec{r} \times \vec{a}))-(\vec{a} \times(\vec{b} \times \vec{a}))+\vec{b} \times(\vec{r} \times \vec{b})-\vec{b} \times(\vec{c} \times \vec{b})+ \\
& \vec{c} \times(\vec{r} \times \vec{c})-(\vec{c} \times(\vec{a} \times c))=0 \\
& \Rightarrow(\vec{a} \cdot \vec{r}) \vec{a}-|\vec{a}|^2 \vec{r}-(\vec{a} \cdot \vec{b}) \vec{a}+|\vec{a}|^2 \vec{b}+(\vec{b} \cdot \vec{r}) \vec{b}-|\vec{b}|^2 \vec{r}- \\
& (\vec{b} \cdot \vec{c}) \vec{b}+|\vec{b}|^2 \vec{c}+(\vec{c} \cdot \vec{r}) \vec{c}-|\vec{c}|^2 \vec{r}-(\vec{c} \cdot \vec{a}) \vec{a}+|\vec{c}|^2 \vec{a}=0 \\
& \Rightarrow x|\vec{a}|^2 \vec{a}+y|\vec{b}|^2 \vec{b}+z|\vec{c}|^2 \vec{c}-\vec{r}\left(|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2\right)+ \\
& |\vec{a}|^2 \vec{b}+|\vec{b}|^2 \vec{c}+|\vec{c}|^2 \vec{a}=0 \\
& \Rightarrow|\vec{a}|^2(x \vec{a}+y \vec{b}+z \vec{c})-3|\vec{a}|^2 \vec{r}+|\vec{a}|^2(\vec{a}+\vec{b}+\vec{c})=0 \\
& \Rightarrow 3 \vec{r}-\vec{r}=\vec{a}+\vec{b}+\vec{c} \\
& \Rightarrow \vec{r}=\frac{1}{2}(\vec{a}+\vec{b}+\vec{c})
\end{aligned}
$
Hence, the answer is $\frac{1}{2}(\vec{a}+\vec{b}+\vec{c})$

Example 5: Let three vector $\vec{a}, \vec{b}$ and $\vec{c}$ be such that $\vec{c}$ is coplanar with $\vec{a}$ and $\vec{b}, \vec{a} \cdot \vec{b}=7$ and $\vec{b}$ is perpendicular to $\vec{c}$, where $\vec{a}=-\hat{i}+\hat{j}+\hat{k}$ and $\vec{b}=2 \hat{i}+\hat{k}$. Then the value of $2|\vec{a}+\vec{b}+\vec{c}|_{\text {is }}^2$ $\qquad$
[JEE MAINS 2021]
Solution

$
\begin{aligned}
\vec{c} & =\lambda(\vec{b} \times(\vec{a} \times \vec{b})) \\
& =\lambda((\vec{b} \cdot \vec{b}) \vec{b}-(\vec{b} \cdot \vec{a}) \vec{b}) \\
& =\lambda(5(-\hat{i}+\hat{j}+\hat{k})+2 \hat{i}+\hat{k}) \\
& =\lambda(-3 \hat{i}+5 \hat{j}+6 \hat{k}) \\
\vec{c} & \cdot \vec{a}=7 \Rightarrow 3 \lambda+5 \lambda+6 \lambda=7 \\
\Rightarrow & \lambda=\frac{1}{2} \\
\therefore & 2\left|\left(\frac{-3}{2}-1+2\right) \hat{i}+\left(\frac{5}{2}+1\right) \hat{j}+(3+1+1) \hat{k}\right|^2 \\
& =2\left(\frac{1}{4}+\frac{49}{4}+25\right)=25+50=75
\end{aligned}
$
Hence, the answer is 75

Summary

The vector triple product helps us understand how three vectors interact in three-dimensional space. It's used in various fields like mechanics, electromagnetism, and geometry to calculate important quantities like torque, magnetic fields, and volumes. Understanding vector triple product helps us to analyze and solve the problems related to real life.