Motion Of Connected Blocks Over Pulley
When two or more blocks are connected by a string and passed over a pulley, the motion of these connected blocks becomes an intriguing topic of study in mechanics. This scenario, often discussed in physics, provides a practical understanding of Newton’s laws of motion, tension in strings, and the dynamics of pulleys. Imagine an elevator system, where the movement of the elevator is controlled by a counterweight connected via a pulley. The principles governing the motion of the connected blocks are the same, ensuring smooth and balanced operation. Understanding this concept not only helps in solving complex problems in physics but also gives insight into everyday machinery, such as cranes, elevators, and conveyor belts, where similar principles are applied.
- Motion of Connected Blocks Over Pulley
- Solved Examples Based on the Motion of Connected Blocks Over Pulley
- Summary
Motion of Connected Blocks Over Pulley
The motion of connected blocks over a pulley is a fundamental concept in mechanics, where two or more masses are connected by a string or rope and interact through a pulley. This setup is often used to study the principles of tension, acceleration, and force distribution. In such systems, the motion of one block affects the motion of the other, leading to a combined motion that can be analyzed using Newton's laws.

Equation of motion for $m_1$
$
F_{n e t}=T-m_1 g=m_1 a
$
Equation of Motion for $m_2$
$
\begin{aligned}
& F_{n e t}=m_2 g-T=m_2 a \\
& a=\frac{\left[m_2-m_1\right] g}{m_1+m_2} \\
& T=\frac{2 m_1 m_2 g}{m_1+m_2}
\end{aligned}
$
1. When One Block is Hanging, the Other is on the Table
$\begin{aligned} a & =\frac{m_2 g}{m_1+m_2} \\ T & =\frac{m_1 m_2 g}{m_1+m_2}\end{aligned}$
2. Three Blocks, Two are Hanging and One is at the Rest on the Smooth Horizontal Table
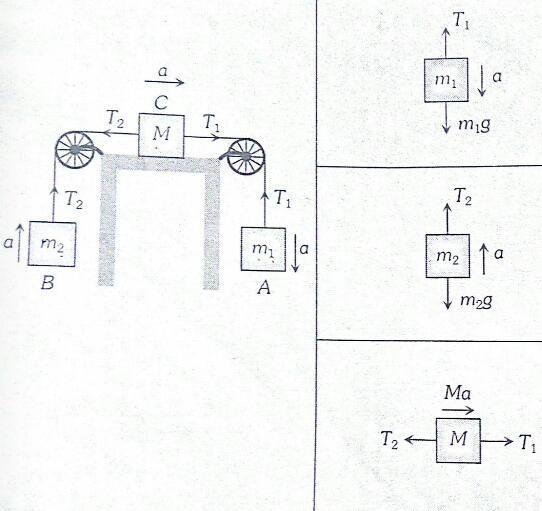
$
\begin{aligned}
& m_1 a=m_1 g-T_1 \\
& m_2 a=T_2-m_2 g \\
& T_1-T_2=M a
\end{aligned}
$
$
\begin{aligned}
& a=\frac{\left(m_1-m_2\right) g}{m_1+m_2+M} \\
& T_1=\frac{m_1\left(2 m_2+M\right) g}{\left(m_1+m_2+M\right)} \\
& T_2=\frac{m_2\left(2 m_1+M\right) g}{\left(m_1+m_2+M\right)}
\end{aligned}
$
Recommended Topic Video
Solved Examples Based on the Motion of Connected Blocks Over Pulley
Example 1. Two masses m1 = 5kg and m2 = 4.8 kg tied to a string are hanging over a light frictionless pulley. What is the acceleration (in m/s2 ) of the masses when lifted free to move?
 ( g = 9.8 m/s2 )
( g = 9.8 m/s2 )
1) 0.2
2) 1.6
3) 0.4
4) 0.8
Solution :

From the free-body diagram,
$T-m_1 g=m_1 a \quad$ - (1)
$m_2 g-T=m_2 a \quad-(2)$
On solving equations (1) and (2)
$\mathrm{a}=\left(\frac{m_1-m_2}{m_1+m_2}\right) \mathrm{g}$
$\mathrm{a}=\frac{0.2}{9.8} \times 9.8=0.2 \mathrm{~m} / \mathrm{s}^2$
Hence the answer is the option (1).
Example 2. A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 ( vertically). If the acceleration of the system is g/8, then the ratio of the masses is
1) 8: 1
2) 9: 7
3) 4: 3
4) 5: 3
Solution :

Given :
$
a=\frac{g}{8}
$
FBD of $m_1$ :

From Newton's 2nd law of motion :
$
\begin{aligned}
& T=m_1 g=m_1 a \\
& T=m_1 g+m_1\left(\frac{g}{8}\right) \\
& T=m_1 g+\frac{m_1 g}{8}=\frac{9 m_1 g}{8}
\end{aligned}
$
FBD of block $m_2$ :

From Newton's 2nd law of motion
$
\begin{aligned}
& m_2 g-T=m_2 a \\
& m_2 g-m_2\left(\frac{g}{8}\right)=T \\
& m_2 g-\frac{m_2 g}{8}=T \\
& \therefore T=\frac{7 m_2 g}{8}
\end{aligned}
$
From (1) and (2),
$
\begin{aligned}
& T=\frac{7 m_2 g}{8}=\frac{9 m_1 g}{8} \\
& \Rightarrow 7 m_2=9 m_1 \\
& \therefore \frac{m_2}{m_1}=\frac{9}{7}
\end{aligned}
$
Hence the answer is the option (2).
Example 3: One end of a massless rope, which passes over a massless and frictionless pulley P is tied to a hook C While the other end is free. The maximum tension that the rope can bear is 960 N. With what value of maximum safe acceleration (in ms-2) can a man of 60 kg climb on the rope?
1) 6
2) 16
3) 4
4) 8
Solution :
FBD of the man is :

From Newton's 2nd law,
$
\begin{aligned}
& T-m g=m a \\
& \text { For } \mathrm{T}=T_{\max } \\
& T_{\max }-m g=m a_{\max } \\
& 960-60 \times 10=60 a_{\max } \\
& \therefore a_{\max }=\frac{360}{60}=6 \mathrm{~m} / \mathrm{s}^2
\end{aligned}
$
Hence the answer is the option (1).
Qu 4. Two blocks of masses m and M are connected using a metal wire of cross-sectional area A passing over a frictionless fixed pulley as shown in the figure. The system is then released. If M=2m, then the stress produced in the wire is :

1) $\frac{2 m g}{3 A}$
2) $\frac{4 m g}{3 A}$
3) $\frac{m g}{A}$
4) $\frac{3 m g}{4 A}$
Solution:
Tension in the wire, $T=\left(\frac{2 m M}{m+M}\right) g$
$
\begin{aligned}
& \text { Stress }=\frac{\text { Force } / \text { Tension }}{\text { Area }}=\frac{2 m M}{A(m+M)} g \\
& (M=2 m \text { given }) \\
& \text { Stress }=\frac{2(m \times 2 m) g}{A(m+2 m)}=\frac{4 m^2}{3 m A} g=\frac{4 m g}{3 A}
\end{aligned}
$
Hence the answer is the option (2).
Summary
The article explores the motion of connected blocks over a pulley, providing a deep understanding of key physics concepts such as Newton's laws, tension, and acceleration. It includes various solved examples, each demonstrating how to calculate acceleration, tension, and other forces in different pulley systems. The problems range from simple scenarios involving two masses to more complex ones, such as determining the stress in a wire or the maximum force a boy can exert without moving a wooden block. These examples illustrate the practical applications of pulley systems in real-world situations.
Frequently Asked Questions (FAQs)
Also Read
02 Jul'25 07:45 PM
02 Jul'25 07:42 PM
02 Jul'25 07:42 PM
02 Jul'25 07:41 PM
02 Jul'25 07:41 PM
02 Jul'25 07:40 PM
02 Jul'25 07:40 PM
02 Jul'25 07:33 PM
02 Jul'25 07:33 PM
02 Jul'25 07:33 PM
