Reaction Of Road On Car
When driving, the reaction of the road on a car is a critical factor that determines how safely and smoothly a vehicle can travel. This reaction, often referred to as road resistance or friction, is the force that the road exerts on the tyres of a car, enabling it to move forward, stop, and turn. Without this reaction, tyres would simply spin without traction, making driving impossible. In real life, you can think of it as trying to walk on ice—without enough friction, your feet would slide uncontrollably. Similarly, the quality of the road surface and the condition of the tyres play a huge role in how well a car can grip the road, impacting everything from acceleration to braking distance. Understanding this interaction between road and car is crucial for ensuring vehicle stability and passenger safety, especially in varying weather conditions like rain or snow.
This Story also Contains
- 1. When the Bridge is Concave
- 2. When the Bridge is Convex
- Solved Examples Based on Reaction of Road on Car
- Summary
1. When the Bridge is Concave
When a bridge is concave, it means that the surface of the bridge curves downward, resembling the shape of a bowl or a segment of a circle that is turned inward. This curvature affects the way forces are distributed across the structure, particularly how vehicles experience the reaction from the road.

$\begin{aligned} & \text { Centripetal force }=R-m g \cos \theta=\frac{m v^2}{r} \\ & \text { Reaction } \mathrm{R}=m g \cos \theta+\frac{m v^2}{r} \\ & \mathrm{R}=\text { reaction } \\ & \mathrm{V}=\text { velocity } \\ & \mathrm{r}=\text { radius }\end{aligned}$
2. When the Bridge is Convex
When a bridge is convex, the surface of the bridge curves upward, creating an arch-like shape. This upward curvature has a significant impact on the distribution of forces across the bridge and the experience of vehicles travelling over it.

$\begin{aligned} & F_{\mathrm{c}}=m g \cos \theta-R=\frac{m v^2}{r} \\ & R=m g \cos \theta-\frac{m v^2}{r} \\ & \mathrm{R}=\text { reaction } \\ & \mathrm{F}_{\mathrm{c}}=\text { centripetal force } \\ & \mathrm{mg}=\text { weight } \\ & \theta=\text { angle of } \mathrm{R} \text { with vertical } \\ & \mathrm{V}=\text { tangential velocity }\end{aligned}$
Recommended Topic Video
Solved Examples Based on Reaction of Road on Car
Example 1: A car is going on a convex bridge with a radius R. The driver maintains a constant speed, as the car ascends on the bridge, the normal force on it:
1) Increases
2) Decrease
3) Remain same
4) Fluctuates
Solution:
Reaction Road on Car When the bridge is convex
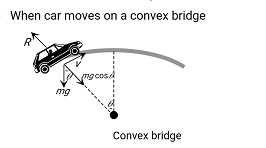
$\begin{aligned} & F_c=m g \cos \theta-R=\frac{m v^2}{r} \\ & R=m g \cos \theta-\frac{m v^2}{r} \\ & \mathrm{R}=\text { reaction } \\ & \mathrm{F}_{\mathrm{c}}=\text { centripetal force } \\ & \mathrm{mg}=\text { weight } \\ & \text { wherein } \\ & \theta=\text { the angle of } \mathrm{R} \text { with the centre } \\ & \mathrm{v}=\text { tangential velocity } \\ & R=m g \cos \theta-\frac{m v^2}{r} \\ & \text { So }\end{aligned}$
So as $\theta$ decreases $\cos \theta$ Increases so R Increases.
Hence, the answer is the option (1).
Example 2: A car moves on a concave bridge of radius R then the maximum reaction force on the car will be:
[ let the mass of the car be m]
1) mg
2) $\frac{m v^2}{R}$
3) $m g-\frac{m v^2}{R}$
4) $m g+\frac{m v^2}{R}$
Solution:
Reaction of Road on Car
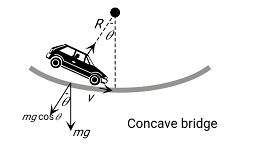
Centripetal force $=R-m g \cos \theta=\frac{m v^2}{r}$
Reaction $\mathrm{R}=m g \cos \theta+\frac{m v^2}{r}$
$R=$ reaction
$\mathrm{V}=$ velocity
$r=$ radius
wherein
It is a case when the car moves on a concave bridge.
the maximum reactor will be at the lowest point of the bridge, so
$
N=m g+\frac{m v^2}{R}
$

Hence, the answer is the option (4).
Example 3: A car of mass m is moving on a concave bridge of radius r with velocity v as shown in the diagram for what value of the reaction on the car by the bridge will be the maximum
Where $\theta$ is the angle made by a vertical line

1) $0^{\circ}$
2) $90^{\circ}$
3) $30^{\circ}$
4) $45^{\circ}$
Solution:
Reaction of Road on Car

Centripetal force $=R-m g \cos \theta=\frac{m v^2}{r}$
Reaction $\mathrm{R}=m g \cos \theta+\frac{m v^2}{r}$
$\mathrm{R}=$ reaction
$\mathrm{V}=$ velocity
$r=$ radius
wherein
It is a case when the car moves on a concave bridge.
For any angle $\theta$
$
R=\frac{m v^2}{r}+m g \cos \theta
$

The maximum value of R will be for the maximum value of
$\begin{gathered}\cos \theta=1 \\ \text { or } \theta=0^{\circ} \\ R=\frac{m v^2}{r}+m g\end{gathered}$
Hence, the answer is the option (1).
Example 4: A car is moving on a convex bridge of radius r with velocity v for what maximum value of v car will lose contact with the bridge
1) $\sqrt{2 r g}$
2) $2 \sqrt{r g}$
3) $\sqrt{r g}$
4) $\frac{1}{2} \sqrt{r g}$
Solution:
Reaction Road on Car When the bridge is convex

$
\begin{aligned}
& F_c=m g \cos \theta-R=\frac{m v^2}{r} \\
& R=m g \cos \theta-\frac{m v^2}{r} \\
& \mathrm{R}=\text { reaction } \\
& \mathrm{F}_{\mathrm{c}}=\text { centripetal force } \\
& \mathrm{mg}=\text { weight }
\end{aligned}
$
wherein
$\theta=$ the angle of R with the centre
$
\mathrm{v}=\text { tangential velocity }
$

$
\begin{aligned}
& R=m g \cos \theta-\frac{m v^2}{r} \\
& R_{\max }=m g-\frac{m v^2}{r}
\end{aligned}
$
To lose the contact $\mathrm{R}=0$
For $v_{\max }, R_{\text {max }}=0$
$
\begin{aligned}
& m g-\frac{m v^2}{r}=0 \\
& v_{\max }=\sqrt{r g}
\end{aligned}
$
Hence, the answer is the option (3).
Example 5: A vehicle of mass 200 kg is moving along a levelled curved road of radius 70 m with an angular velocity of 0.2 rad/s. The centripetal force acting on the vehicle is:
1) 2800 N
2) 560 N
3) 2240 N
4) 14 N
Solution:
$\begin{aligned} & F_c=m \omega^2 r=200 \times(0.2)^2 \times 70 \\ & =560 \mathrm{~N}\end{aligned}$
Hence, the answer is the option (2).
Summary
The article discusses the reaction of the road on a car, particularly focusing on how the curvature of bridges—concave or convex—affects vehicle dynamics. It explains the distribution of forces, such as centripetal force and normal reaction, on vehicles traveling over these curved surfaces. The article also provides solved examples to illustrate how these forces change based on the shape of the bridge and the speed of the vehicle, impacting safety and stability.