• Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • School
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
Addition And Subtraction Of Algebraic Expression

Addition And Subtraction Of Algebraic Expression

Team Careers360Updated on 02 Jul 2025, 05:17 PM IST

Algebraic expression addition and subtraction are slightly more complicated than natural number operations. In order to learn the addition and subtraction of algebraic expressions, first we have to understand the algebraic expression. An algebraic expression is just an equation containing a combination of constants and variables.

This Story also Contains

  1. Algebraic Expressions Addition And Subtraction
  2. Horizontal Addition
  3. Vertical Addition
  4. Horizontal Subtraction
  5. Vertical Subtraction

Let us take an example of algebraic expression: suppose your teacher asked you to convert the statement “Marks obtained by student A of class 10th is 10 marks more than the marks obtained by student B of 10th “ into mathematical form.

Now to express it in mathematical form suppose marks obtained by A are x and marks obtained by B are y now according to the statement x is 10 more than y.

In mathematical form, we write the above statement as

x=y+10

This expression is known as an Algebraic expression.

Algebraic Expressions Addition And Subtraction

In mathematics addition, subtraction and other mathematical operations are easily applicable to natural numbers. If we talk about mathematical operations on algebraic expressions it is not the same as in natural numbers. While applying addition and subtraction to algebraic expressions we must keep in mind that only terms which are having the same variable and exponent will be added or subtracted. We have to follow some steps for applying mathematical operations to an algebraic expression.

Methods of addition and subtraction are:

  1. Horizontal

  2. Vertical

Commonly Asked Questions

Q: What is an algebraic expression?
A:
An algebraic expression is a combination of variables, numbers, and mathematical operations. It can include letters representing unknown values, constants, and symbols for addition, subtraction, multiplication, or division. For example, 3x + 2y - 5 is an algebraic expression.
Q: How do you identify like terms in algebraic expressions?
A:
Like terms are terms that have the same variables raised to the same powers. To identify like terms, look for terms with identical variable parts. For example, in the expression 3x + 2y + 5x - 4, 3x and 5x are like terms because they both have x to the first power.
Q: Why can't we add or subtract terms with different variables?
A:
We can't add or subtract terms with different variables because they represent different quantities. It's similar to how we can't add apples and oranges directly. We can only combine like terms, which have the same variable parts.
Q: How do you simplify an expression like 3x + 2y - 4x + 5y?
A:
To simplify this expression, combine like terms: group terms with x and terms with y. 3x + 2y - 4x + 5y = (3x - 4x) + (2y + 5y) = -x + 7y.
Q: What is the zero principle in algebra, and how does it relate to addition and subtraction?
A:
The zero principle states that adding or subtracting zero from any quantity doesn't change its value. In algebra, this means that terms like +0x or -0y can be added or removed without affecting the expression's value. This principle is often used in simplification.

Horizontal Addition

Steps in addition

  1. Write each algebraic expression within a bracket in a single row with a plus sign in between them.

  2. Now open all the brackets.

  3. Write terms having the same variable and exponent with the appropriate sign in a bracket.

  4. Add the coefficient of all the terms having the same variable and exponent.

To understand the above steps let us take an example of algebraic addition

First expression- \[2x + 3y + 1\] 1706458076053

Second expression- \[10x + 13y + 5\]1706458075919

Follow above steps

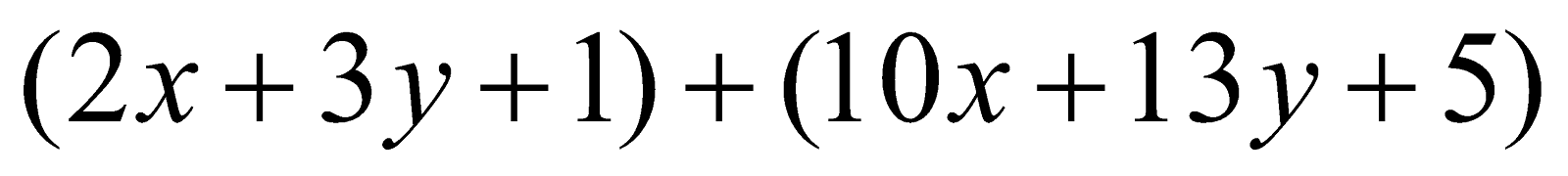
  1. \[(2x + 3y + 1) + (10x + 13y + 5)\] 1706458074840

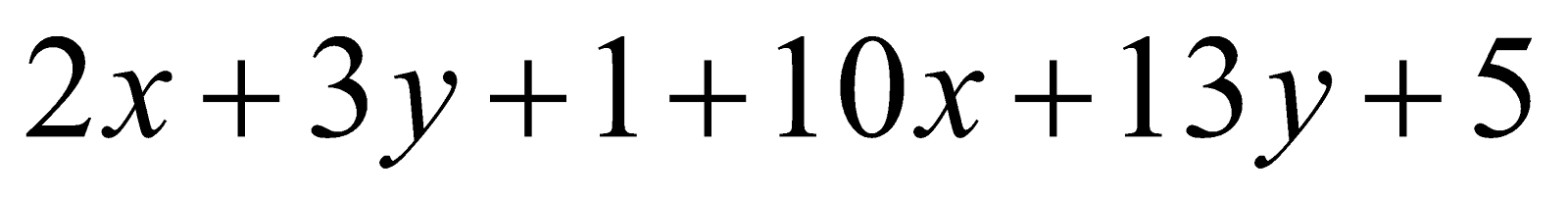
  2. \[2x + 3y + 1 + 10x + 13y + 5\] 1706458074651

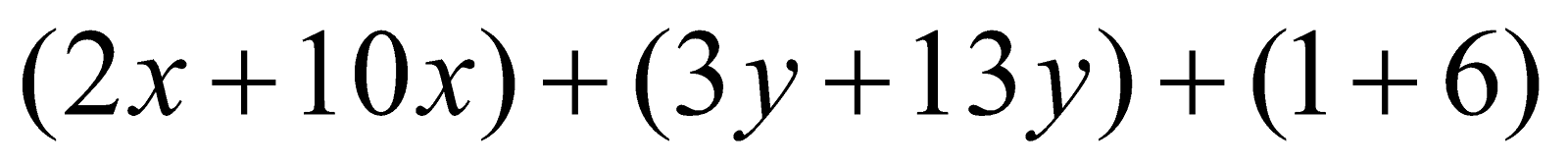
  3. \[(2x + 10x) + (3y + 13y) + (1 + 6)\] 1706458074288

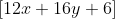
  4. \[12x + 16y + 6\] 1706458073204

JEE Main Highest Scoring Chapters & Topics
Focus on high-weightage topics with this eBook and prepare smarter. Gain accuracy, speed, and a better chance at scoring higher.
Download E-book

Vertical Addition

In this method, we have to write each expression in a different row. While writing expressions in different rows keep in mind that the terms having the same variables and exponent must be written one below the others along with their sign. Now we have to add all coefficients present in a particular column to get the value of the addition.

To understand the above steps let us take an example of algebraic addition

First expression- \[2x + 3y + 1\] 1706458076419

Second expression-\[10x + 13y + 5\] 1706458075586

Now add these two by using the vertical method

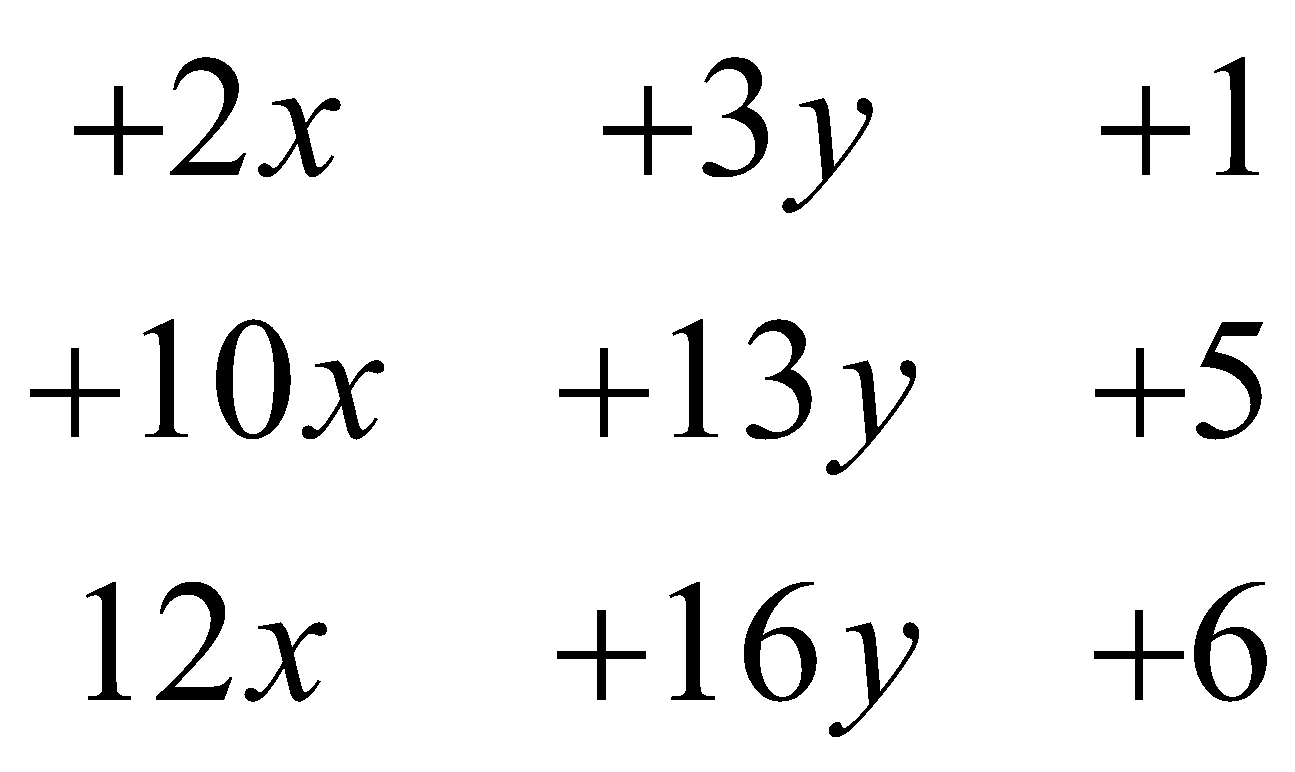
1706458074034

\begin{array}{ccc}

+2 x & +3 y & +1 \\

+10 x & +13 y & +5 \\

12 x & +16 y & +6

\end{array}

Horizontal Subtraction

Steps in subtraction

  1. Write each algebraic expression within a bracket in a single row with a minus sign in between them.

  2. Now open all brackets and apply the algebra of the sign of a term.

  3. Write terms having the same variable and exponent with the appropriate sign in a bracket.

  4. Subtract the coefficient of all the terms having the same variable and exponent.

To understand the above steps let us take an example of algebraic addition

First expression- 1706458076552

Second expression- 1706458075675

Now subtract first from second by using the horizontal method

Follow above steps

  1. 1706458074119

  2. 1706458073604

  3. 1706458073849

  4. 1706458076781

First expression- \[2x + 3y + 1\]

Second expression- \[10x + 13y + 5\]

Follow above steps

  1. \[(2x + 3y + 1) - (10x + 13y + 5)\]

  2. \[2x + 3y + 1 - 10x - 13y - 5\]

  3. \[(2x - 10x) + (3y - 13y) + (1 - 5)\]

  4. \[ - 8x - 10y - 4\]

Vertical Subtraction

In this method, we have to write each expression in a different row. While writing expressions in different rows keep in mind that the terms having the same variables and exponent must be written one below the others along with their sign. Now we have to subtract all coefficients present in a particular column to get the value of the addition.

Let us take an example to understand it

First expression- 1706458076302

Second expression- 1706458077087

Now subtract first from second by using the vertical method

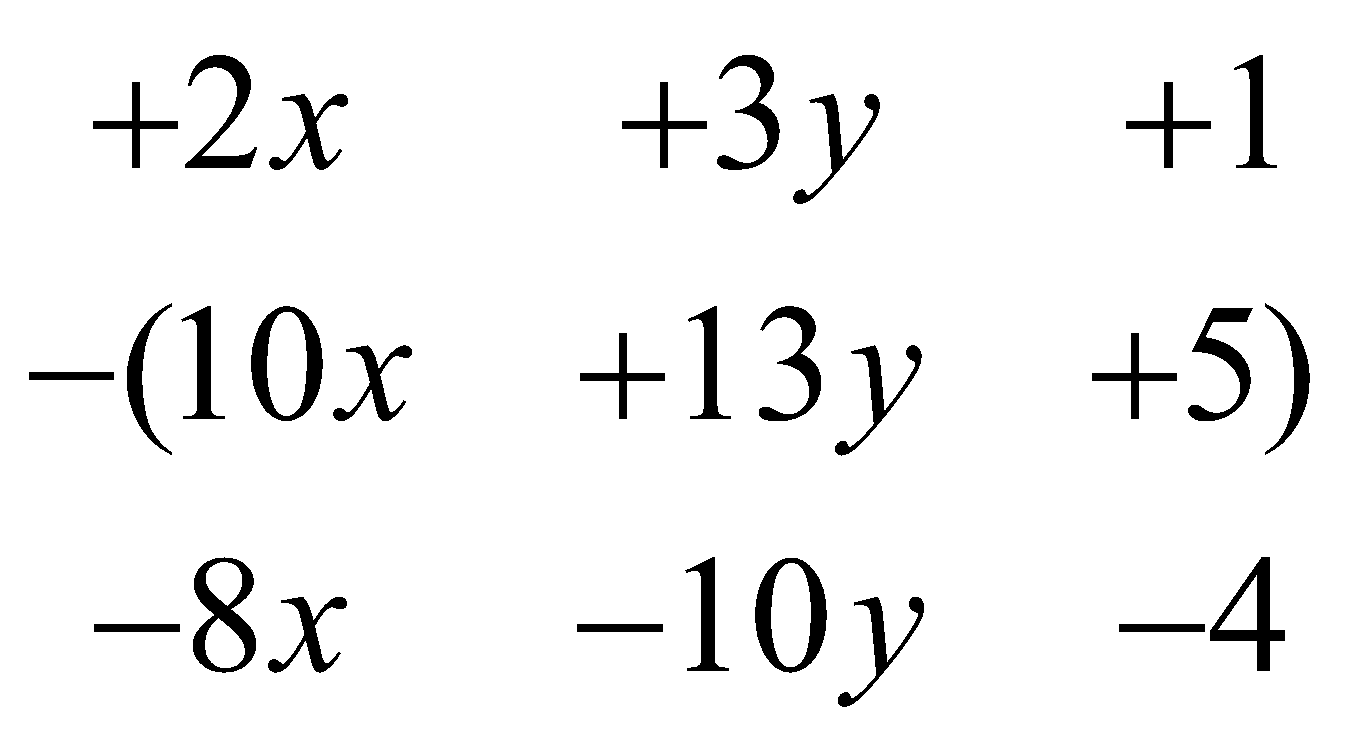
1706458077178

First expression- \[2x + 3y + 1\]

Second expression- \[10x + 13y + 5\]

Now subtract first from second by using vertical method

\begin{array}{ccc}

+2 x & +3 y & +1 \\

-(10 x & +13 y & +5) \\

-8 x & -10 y & -4

\end{array}

Commonly Asked Questions

Q: What common mistake do students make when subtracting expressions with parentheses?
A:
A common mistake is forgetting to change the signs of all terms inside the parentheses when subtracting. For example, in 5x - (2x + 3), students might incorrectly write 5x - 2x + 3 instead of the correct 5x - 2x - 3.
Q: How do you handle negative coefficients when adding or subtracting algebraic expressions?
A:
Treat negative coefficients as you would negative numbers in arithmetic. When adding, keep the sign. When subtracting, change the sign. For example, 3x + (-2x) = x, and 3x - (-2x) = 3x + 2x = 5x.
Q: How do you add or subtract algebraic fractions?
A:
To add or subtract algebraic fractions, find a common denominator, then add or subtract the numerators while keeping the common denominator. For example, (x/2) + (y/3) = (3x/6) + (2y/6) = (3x + 2y)/6.
Q: How does subtracting an algebraic expression differ from adding its negative?
A:
Subtracting an algebraic expression is equivalent to adding its negative. For example, subtracting (3x - 2) is the same as adding (-3x + 2). This principle is based on the fact that subtracting a positive number is the same as adding a negative number.
Q: What is the concept of "cancelling out" in algebraic addition and subtraction?
A:
"Cancelling out" occurs when adding or subtracting terms results in a coefficient of zero, effectively eliminating that term. For example, in 5x - 2y + 3x - 5x, the x terms cancel out: (5x + 3x - 5x) - 2y = 3x - 2y.

Frequently Asked Questions (FAQs)

Q: What is the concept of "zero pairs" in algebraic addition and subtraction?
A:
Zero pairs are terms that add up to zero, such as x and -x. Identifying and cancelling zero pairs can simplify expressions. For example, in 3x + 2y - x + 4, x and -x form a zero pair, leaving 2x + 2y + 4.
Q: How do you handle addition and subtraction of algebraic expressions with different variable representations (e.g., x vs. x(t))?
A:
Variables with different representations are treated as distinct variables. For example, x and x(t) cannot be combined as like terms. The expression 3x + 2x(t) cannot be simplified further unless additional information is provided about the relationship between x and x(t).
Q: How do you add or subtract algebraic expressions involving matrices?
A:
Matrix addition and subtraction are performed element by element, and only matrices of the same dimensions can be added or subtracted. For example, if A = [1 2; 3 4] and B = [5 6; 7 8], then A + B = [6 8; 10 12].
Q: What is the concept of "dimensional analysis" in algebraic addition and subtraction?
A:
Dimensional analysis ensures that only quantities with the same dimensions (units) are added or subtracted. For example, you can add lengths to lengths, but not lengths to areas. This principle helps in checking the validity of algebraic operations in physics and engineering problems.
Q: How do you handle addition and subtraction of algebraic expressions with different number bases?
A:
Convert all terms to the same base before adding or subtracting. For example, to add a binary number 1010₂ and a decimal number 6₁₀, convert both to the same base: 1010₂ = 10₁₀, so 10₁₀ + 6₁₀ = 16₁₀.
Q: What is the importance of order of operations (PEMDAS/BODMAS) in algebraic addition and subtraction?
A:
The order of operations ensures consistent evaluation of expressions. In the context of addition and subtraction, it's crucial to perform operations within parentheses first, then exponents, followed by multiplication and division (from left to right), and finally addition and subtraction (from left to right).
Q: How do you add or subtract algebraic expressions involving logarithms?
A:
Logarithms with the same base and argument can be combined by adding or subtracting their coefficients. For example, 2 log₃(x) - log₃(x) = log₃(x). However, log₃(x) + log₃(y) cannot be combined further using addition or subtraction.
Q: What is the concept of "like bases" in exponential expressions, and how does it relate to addition and subtraction?
A:
Terms with like bases but different exponents cannot be combined through addition or subtraction. For example, 2³ + 2⁴ cannot be simplified further. However, if the exponents are the same, you can add or subtract the coefficients: 3 × 2³ + 2 × 2³ = 5 × 2³.
Q: How do you handle addition and subtraction of algebraic expressions with imaginary numbers?
A:
Treat imaginary numbers like any other term, but keep the imaginary unit i separate. For example, (3 + 2i) + (4 - 5i) = 7 - 3i. Remember that i² = -1, but don't combine i terms with real terms.
Q: What is the role of the associative property in simplifying complex algebraic additions?
A:
The associative property allows us to group terms in different ways without changing the result. This is useful in simplifying complex expressions. For example, (a + b) + c = a + (b + c), which can make calculations easier depending on the values involved.
Articles
Previous
Next