• Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • School
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
Algebra Formulas For Class 8

Algebra Formulas For Class 8

Team Careers360Updated on 02 Jul 2025, 05:16 PM IST

Algebraic Formulas are algebraic equations which are true for each and every value of the variable in it. The algebraic formulas that are valid for all values of variables in it are called algebraic identities. These identities are used to factorize polynomials and are used to compute algebraic expressions and solve different polynomials.

Algebraic expressions are known as collections of constants and variables connected to one or more operations like addition, subtraction, multiplication, and division. This expression contains monomial, binomial, trinomial and multinomial.Here monomial means having one term, binomial means having two terms, trinomial means having three terms, and multinomial means having more than three terms.

  • Constants which means a symbol having a fixed value.

  • Variables are collections of symbols that can give various numerical values.

  • Factor means quantities multiplied by each other to give a product and that product is known as a factor.

  • A factor of a non-constant term of an algebraic expression is called the coefficient of the remaining factor of a term. And these coefficients are of two types one is a numerical coefficient and another one is a literal coefficient.

Polynomials are of three types:

  • Linear polynomials having degree one.

  • Quadratic polynomial having degree two.

  • Cubic polynomial having degree three.

Algebraic Formulas

  1. (a + b)^{2} = a^{2} + 2ab + b^{2}

JEE Main Highest Scoring Chapters & Topics
Focus on high-weightage topics with this eBook and prepare smarter. Gain accuracy, speed, and a better chance at scoring higher.
Download E-book

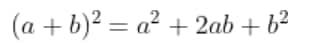
1706450956861

  1. (a - b)^{2} = a^{2} - 2ab + b^{2}

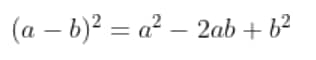
1706450957577

  1. (a+b)(a - b) = a^{2} - b^{2}

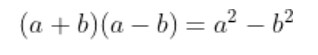
1706450957271

  1. (x+a)(x+b) = x^{2} + (a+b)x + ab

1706450957677

  1. (x+a)(x-b) = x^{2} + (a-b)x - ab

1706450957068

  1. (x-a)(x+b) = x^{2} + (b-a)x - ab

1706450956786

  1. (x-a)(x-b) = x^{2} - (a+b)x + ab

1706450957120

  1. (a+b)^{3} = a^{3} + b^{3} + 3ab(a+b)

1706450957019

  1. (a-b)^{3} = a^{3} - b^{3} - 3ab(a-b)

1706450957471

  1. (a+b+c)^{2} = a^{2} + b^{2} + c^{2} + 2ab + 2bc + 2ac

1706450957220

  1. (a+b-c)^{2} = a^{2} + b^{2} + c^{2} + 2ab - 2bc - 2ac

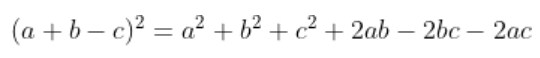
1706450957424

  1. (a-b+c)^{2} = a^{2} + b^{2} + c^{2} - 2ab - 2bc + 2ac

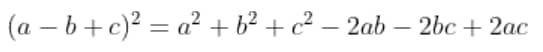
1706450957325

  1. (a-b-c)^{2} = a^{2} + b^{2} + c^{2} - 2ab + 2bc - 2ac

1706450956968

Examples

(x+2)(x+5)

To solve this we can use a formula called: (x+a)(x+b) = x^{2} + (a+b)x + ab

1706450957630

Here a = 2 and b = 5


(x+2)(x+5) = x^{2} + (2+5)x + 10

1706450957524

(x+2)(x+5) = x^{2} + (7)x + 10

1706450956915

Hence, (x+2)(x+5) equals to x^{2} + (7)x + 10.

  1. (x-3)(x+7)

To solve this we can use a formula called: (x-a)(x+b) = x^{2} + (b-a)x - ab

1706450956731

Here a = 3 and b = 7


(x-3)(x+7) = x^{2} + (7-3)x - 21

1706450957372


(x-3)(x+7) = x^{2} + 4x - 21


1706450957167


Hence, (x-3)(x+7) equals to x^{2} + 4x - 21.

Commonly Asked Questions

Q: What is the FOIL method, and when is it used?
A:
FOIL (First, Outer, Inner, Last) is a mnemonic device for multiplying two binomials. It reminds you to multiply each term of one binomial by each term of the other. For example, (x + 2)(x - 3) = x² - 3x + 2x - 6 = x² - x - 6. It's used specifically for binomial multiplication but is just a special case of the distributive property.
Q: What is a polynomial and how is it different from other algebraic expressions?
A:
A polynomial is an algebraic expression consisting of variables and coefficients, using only addition, subtraction, and multiplication operations. Unlike other algebraic expressions, polynomials do not involve division by variables or negative exponents. For example, 3x² + 2x - 5 is a polynomial, while 2x / (x+1) is not.
Q: How can you determine the degree of a polynomial with multiple variables?
A:
The degree of a polynomial with multiple variables is the highest sum of exponents in any term. For example, in the polynomial 2x²y³ + 3xy² - 5, the degree is 5 because the term x²y³ has the highest sum of exponents (2 + 3 = 5).
Q: Can a constant be considered a polynomial? Why or why not?
A:
Yes, a constant can be considered a polynomial. It's a special case where the degree is 0. For example, 5 can be thought of as 5x⁰, which is a polynomial of degree 0. This concept is important when working with polynomial operations and equations.
Q: How do you add or subtract polynomials, and why does it work?
A:
To add or subtract polynomials, you combine like terms (terms with the same variables and exponents). This works because of the distributive property and the fact that you can only add or subtract similar quantities. For example, (3x² + 2x - 1) + (x² - 3x + 4) = 4x² - x + 3.

Frequently Asked Questions (FAQs)

Q: Why is the discriminant useful in analyzing quadratic polynomials?
A:
The discriminant (b² - 4ac for ax² + bx + c) is useful because:
Q: Why is the concept of a polynomial identity important?
A:
A polynomial identity is an equation that is true for all values of its variables. It's important because:
Q: How does the Rational Root Theorem help in finding polynomial roots?
A:
The Rational Root Theorem states that if a polynomial equation with integer coefficients has a rational solution, it will be of the form ±p/q, where p is a factor of the constant term and q is a factor of the leading coefficient. This narrows down the possible rational roots, making it easier to find them through testing or other methods.
Q: How do you interpret the graph of a polynomial in terms of its algebraic properties?
A:
The graph of a polynomial reveals several algebraic properties:
Q: What's the relationship between a polynomial's degree and its end behavior?
A:
A polynomial's end behavior (its graph's tendency as x approaches ±∞) is determined by its degree and leading coefficient:
Q: How do you determine the multiplicity of a root without fully factoring the polynomial?
A:
To determine a root's multiplicity without full factoring:
Q: How does the concept of a polynomial's turning points relate to its derivative?
A:
A polynomial's turning points (local maxima and minima) are closely related to its derivative:
Q: What's the significance of the Rational Zero Theorem in polynomial algebra?
A:
The Rational Zero Theorem is significant because:
Q: Why can't you cancel terms when adding fractions with polynomial numerators?
A:
You can't cancel terms when adding fractions with polynomial numerators because the terms are being added, not multiplied. Cancellation only applies to factors, not terms. For example, in (x² + 3) / 5 + (2x - 1) / 5, you can't cancel the x² with the 2x; instead, you add the numerators: (x² + 3 + 2x - 1) / 5.
Q: How does factoring relate to the roots of a polynomial equation?
A:
Factoring a polynomial reveals its roots. When you factor a polynomial and set each factor to zero, you find the values of x that make the polynomial equal to zero. These values are the roots of the polynomial equation. For example, if x² - 4 = 0 factors to (x+2)(x-2) = 0, the roots are x = 2 and x = -2.
Articles
Previous
Next