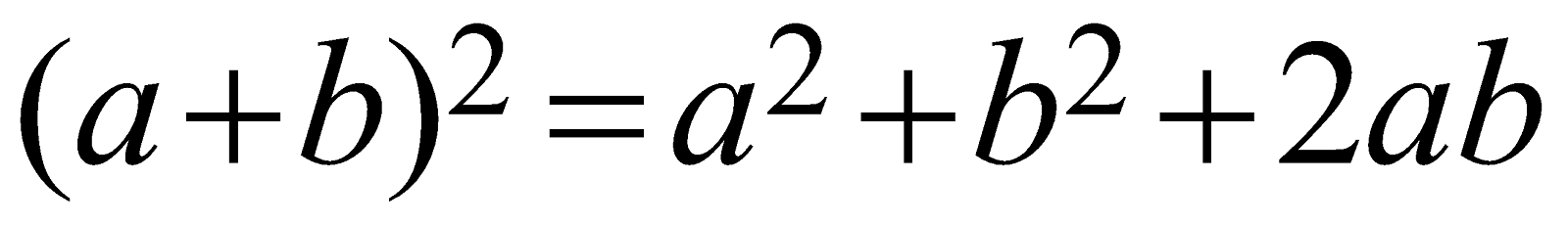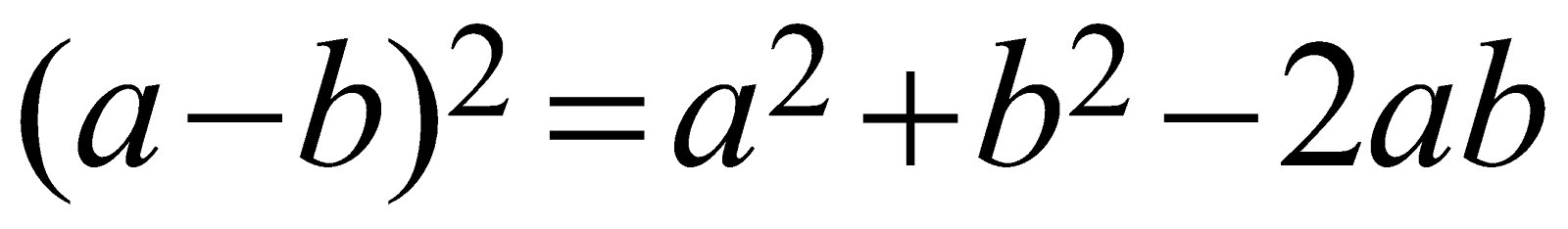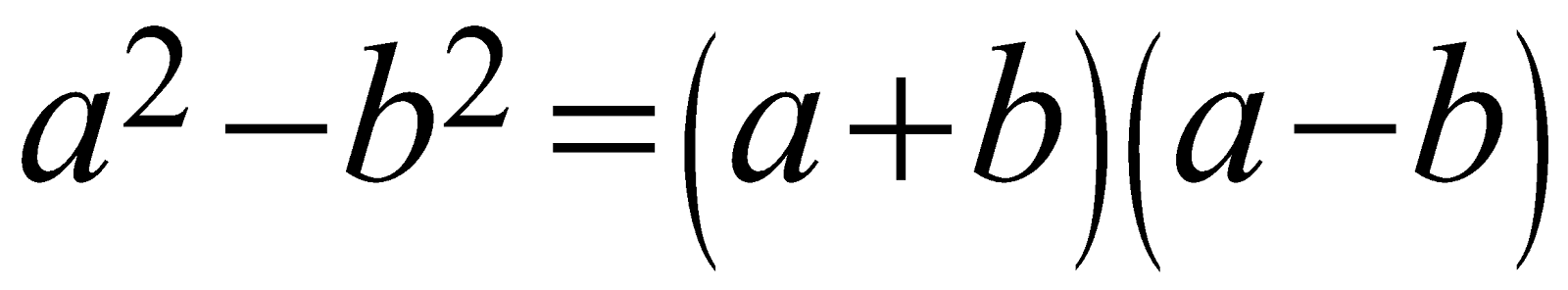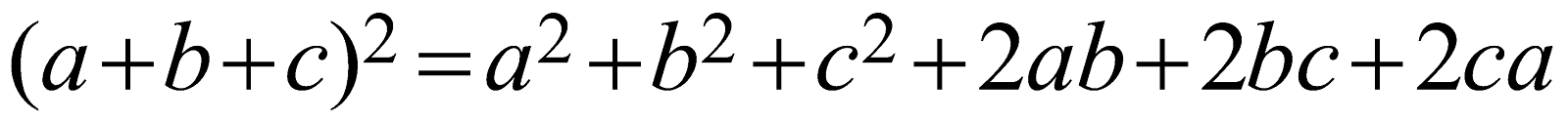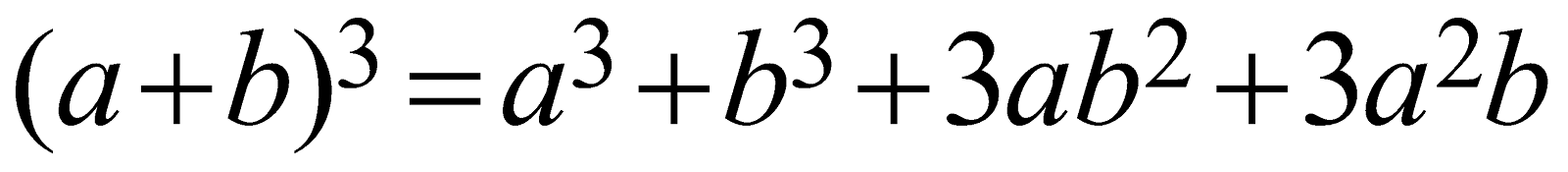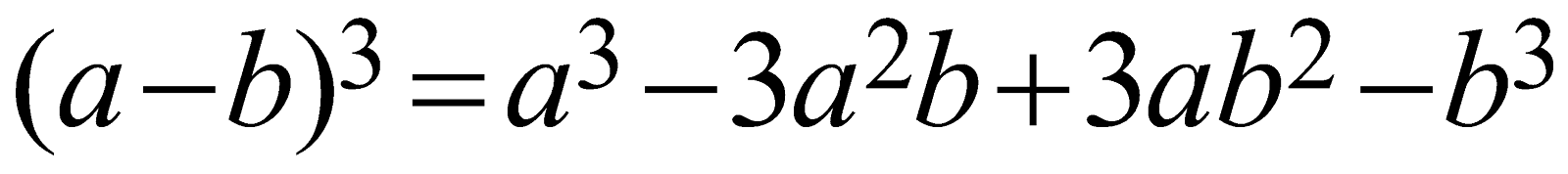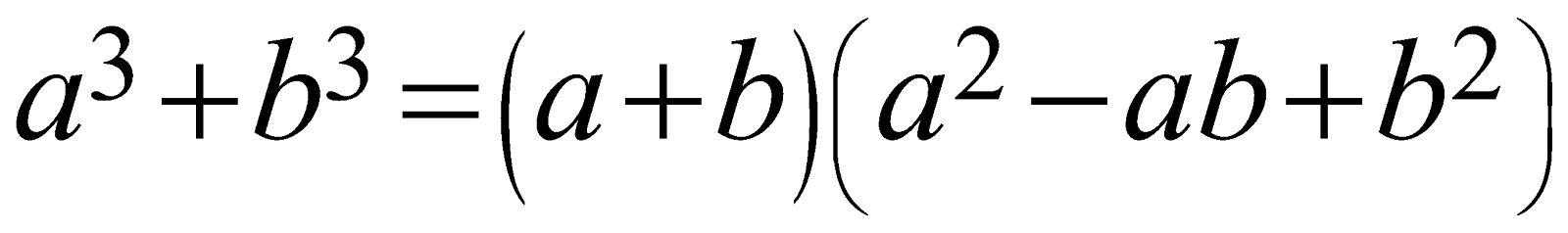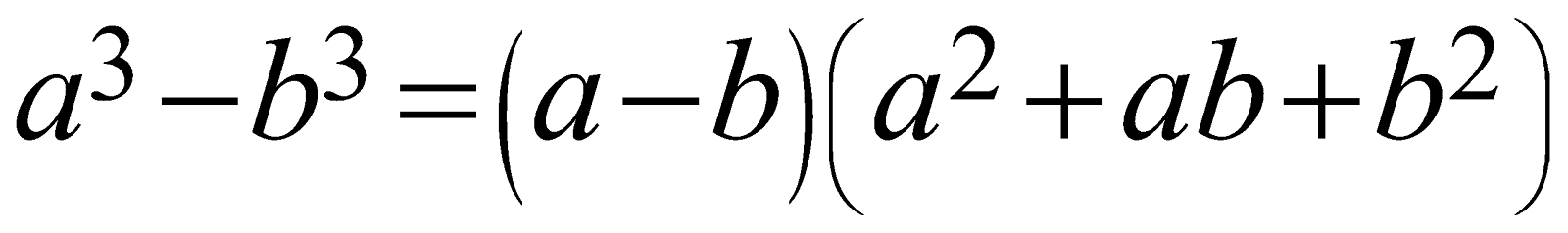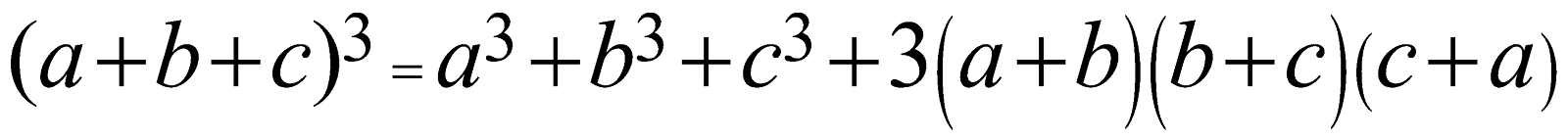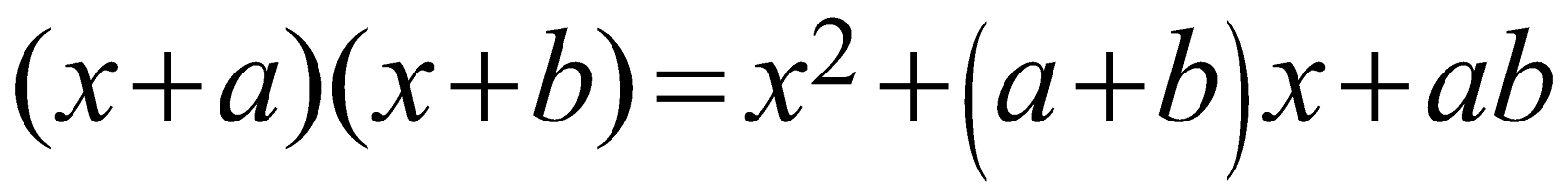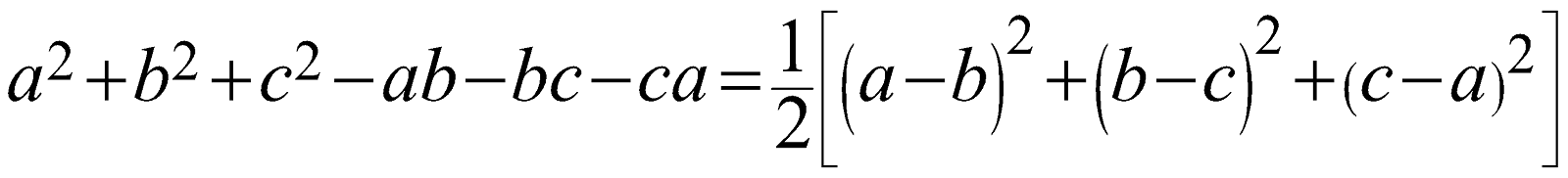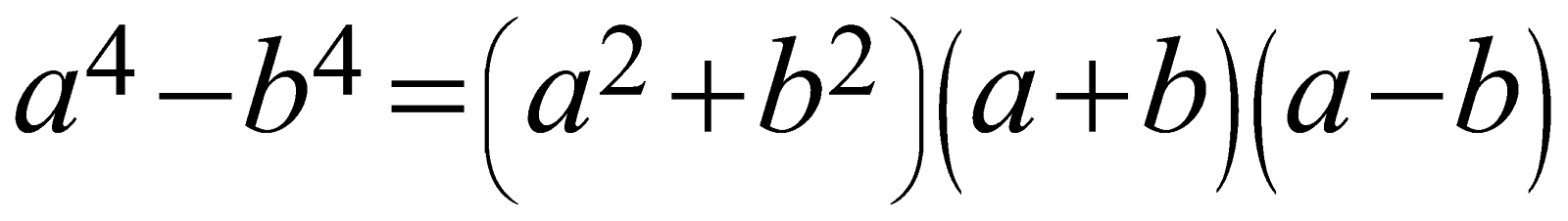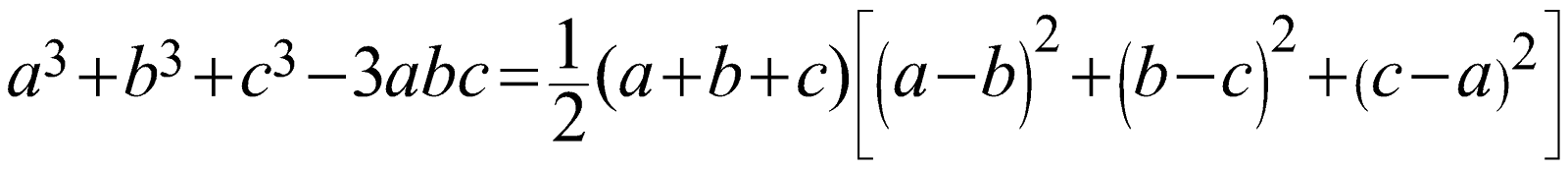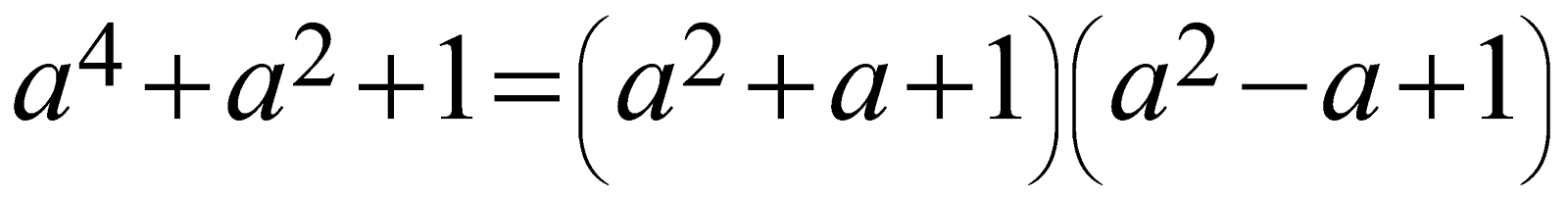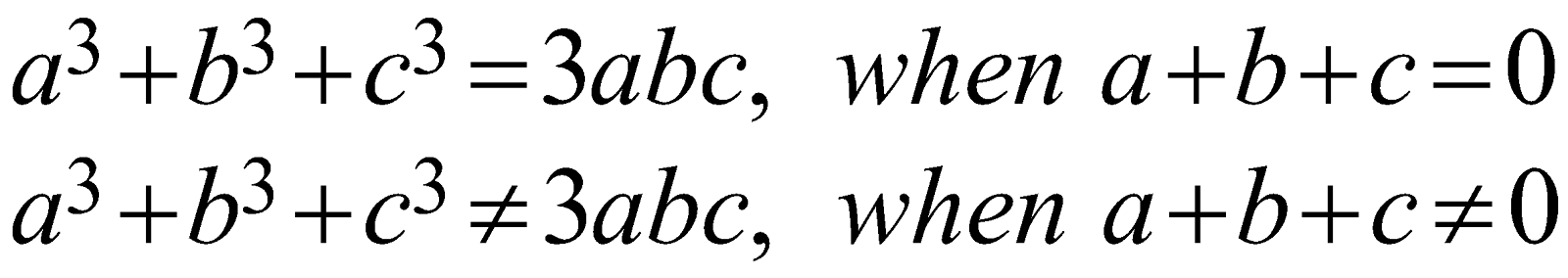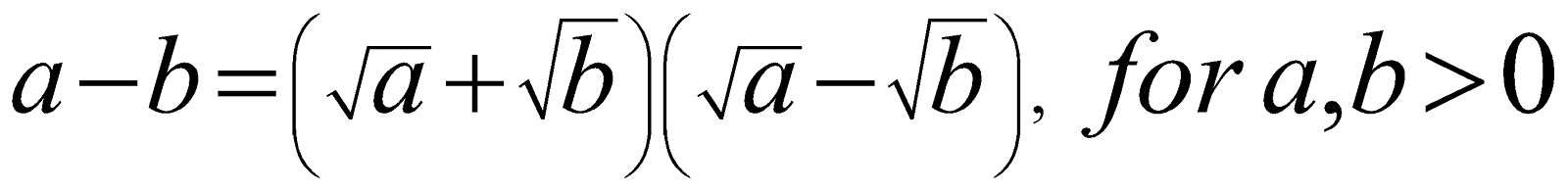Algebraic Expressions Worksheets
Two or more algebraic expressions use the comparator signs among themselves to become an algebraic equation or an algebraic identity. There are various algebraic identities that are helpful in solving problems on simplifications and expansions. All these algebraic standard formats display the commonly used mathematical operators. They represent the mathematical statements in terms of the common operations of division, multiplication, addition, subtraction, and exponentiation. For example, 5{{x}^{2}}-2xy+c ![]() , is an algebraic expression.
, is an algebraic expression.
This Story also Contains
- What Are Mathematical Expressions?
- What Are Algebraic Expressions?
- What Are Equations?
- What Are Algebraic Equations?
- What Are Identities?
- What Are Algebraic Identities?
- What Are The Properties of Algebraic Identities?
- What Are Algebraic Polynomials?
- Chart Of Identities Of Factorization Of Polynomials
- Chart Of Algebraic Identities
Let us explore this article to realize the concept of “algebraic expressions” clearly.
What Are Mathematical Expressions?
The term “mathematical expression” implies a symbolic presentation of any valid mathematical statement, which may include any combination of mathematical operations like division, multiplication, addition, subtraction, and exponentiation as indicated by the corresponding mathematical operators.
The following are examples of mathematical expressions.
\begin{aligned}
& 1) \sqrt{3}+2 \\
& 2) a x^2+b \\
& 3) y^3+3
\end{aligned}
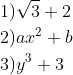
What Are Algebraic Expressions?
The mathematical expression that contains “algebraic Variables”, “coefficients”, and “constants” in any combination is called an “algebraic expression.
Get a clear idea with the following examples.
The mathematical expression \[\sqrt{3}+2\]
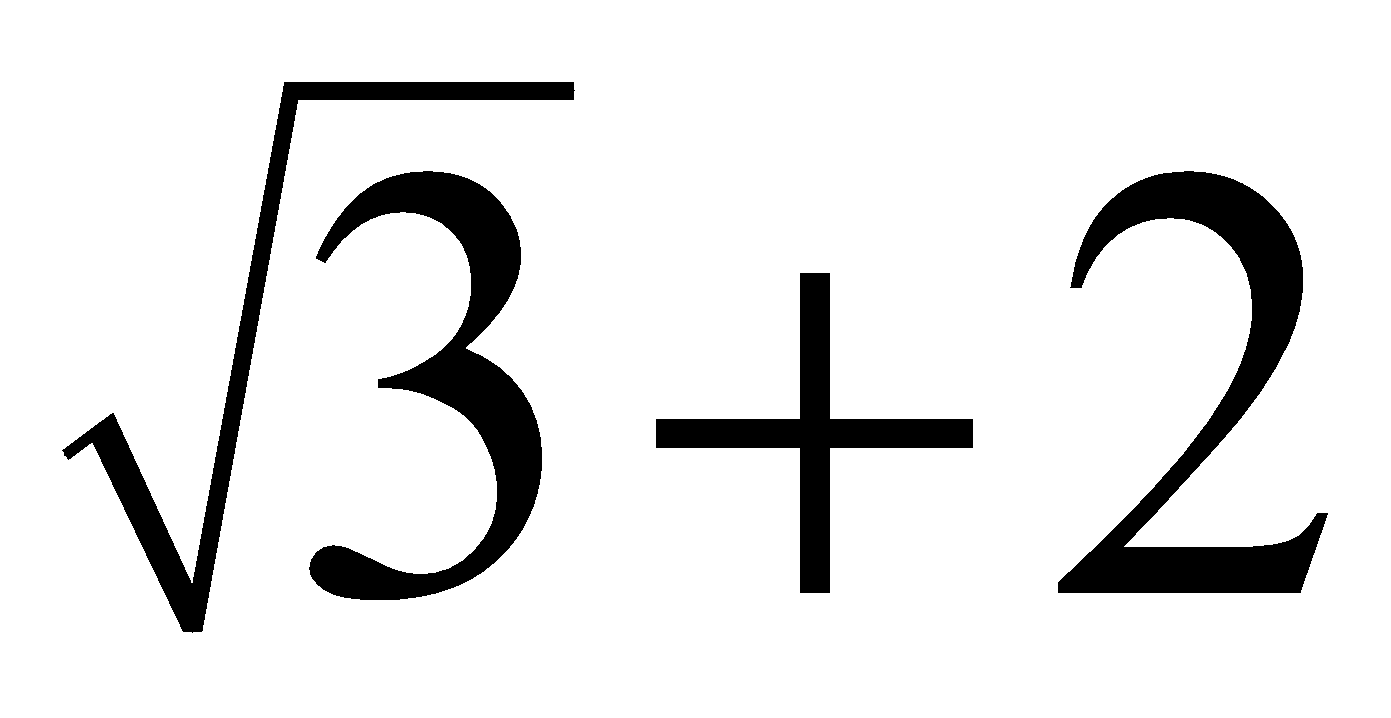 is not an “algebraic expression” but a numeric expression.
is not an “algebraic expression” but a numeric expression.The mathematical expressions \[a{{x}^{2}}+b,\ \ {{y}^{3}}+3\]
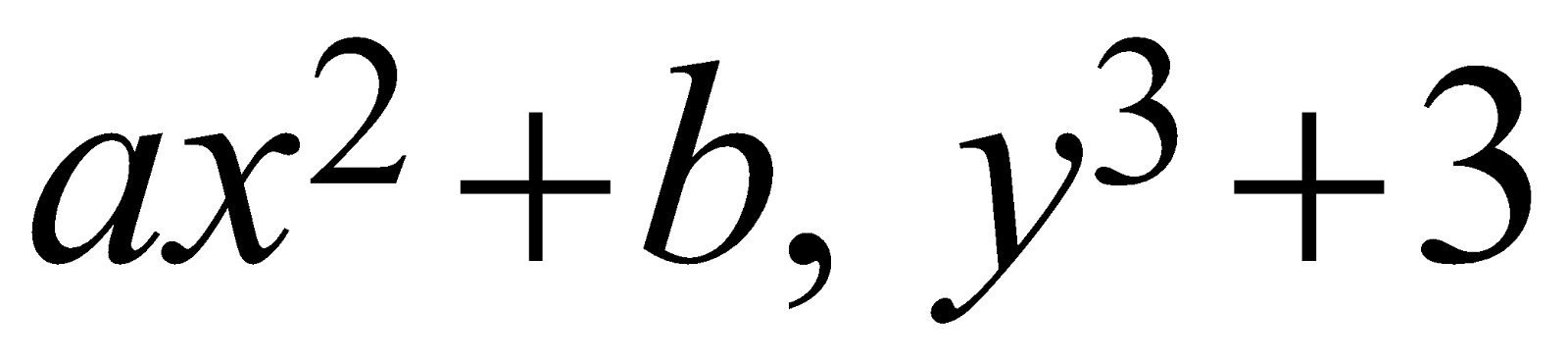 are all “algebraic expressions”.
are all “algebraic expressions”.
What Are Equations?
Suppose, you use the “equal to symbol” represented as “=” to unite any two expressions. The resulting mathematical entity is what you call an “equation”. An equation, basically, tells that two expressions on either side of the “=” are equivalent.
The following are examples of equations.
\begin{aligned}
&1) \sqrt{3} \tan \theta+2=\cos \alpha \\
& 2) a x^2+b=c \\
& 3) y^3=3 \\
& 4) \cos ^3 \theta+3=\sin ^2 \theta
\end{aligned}
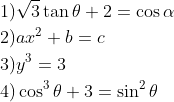
What Are Algebraic Equations?
Suppose, you use the “equal to sign” symbolized as “=” to unite any two algebraic expressions or an algebraic expression to any constant. The subsequent mathematical entity is what you declare an “algebraic equation”. An algebraic equation, actually suggests that the terms on either side of the “=” are equivalent.
Get a clear idea with the next examples.
The mathematical equations \[\sqrt{3}\tan \theta +2=\cos \alpha ,\ \ {{\cos }^{3}}\theta +3={{\sin }^{2}}\theta \]
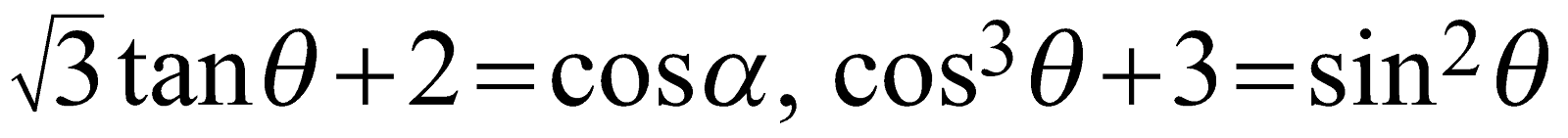 are not “algebraic equations” but are “trigonometric equations”.
are not “algebraic equations” but are “trigonometric equations”.The mathematical equations \[a{{x}^{2}}+b=c,\ \ {{y}^{3}}=3\]
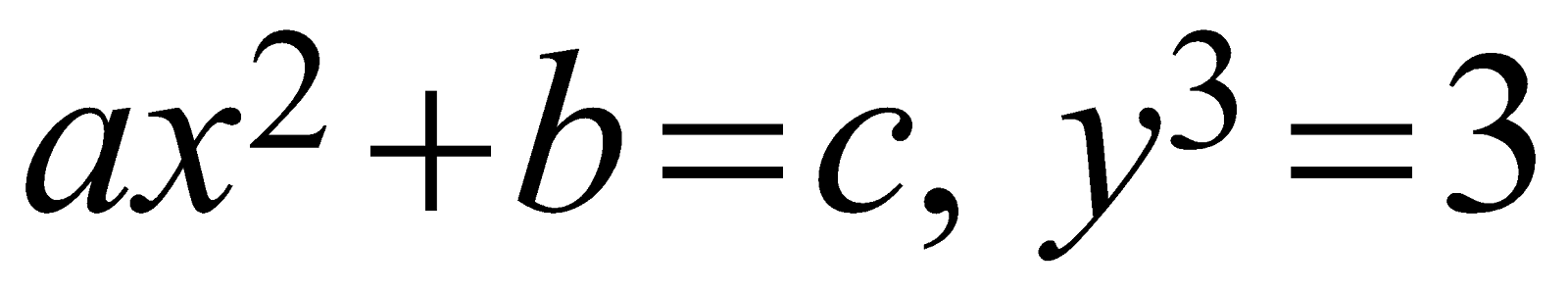 are all “algebraic equations”.
are all “algebraic equations”.
What Are Identities?
Identities are those mathematical entities which are true for any value of the variables involved in one or both the expressions on either side of the “=”.
Following are examples of identities.
\begin{aligned}
& (a+b)^2=a^2+b^2+2 a b \\
& \cos ^2 \theta+\sin ^2 \theta=1
\end{aligned}
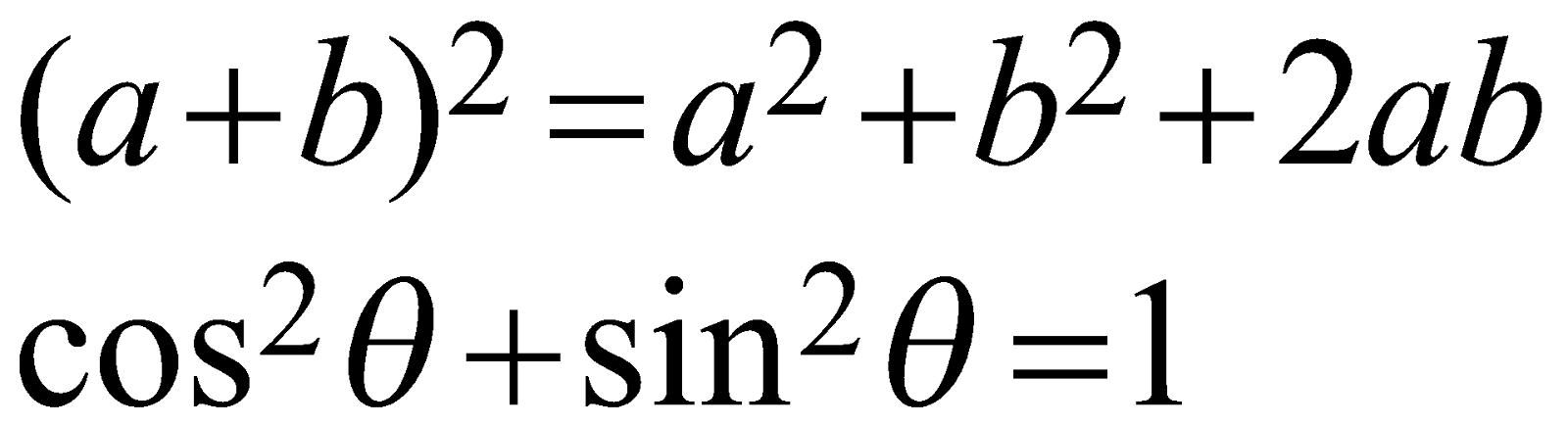
What Are Algebraic Identities?
The identities which involve only the algebraic expressions and may contain coefficients of variables and constants are called “algebraic identities”.
Algebraic identities hold good for any value of the algebraic variables involved in one or both the expressions on either side of the “=”.
Get a perfect idea with the following examples.
The mathematical identity \[{{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1\]
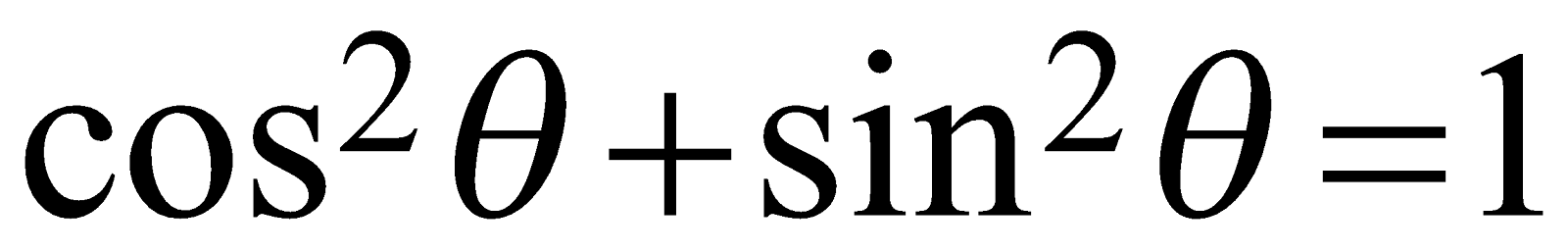 is not an “algebraic identity” but a “trigonometric identity”.
is not an “algebraic identity” but a “trigonometric identity”.The mathematical identity \[{{(a+b)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\]
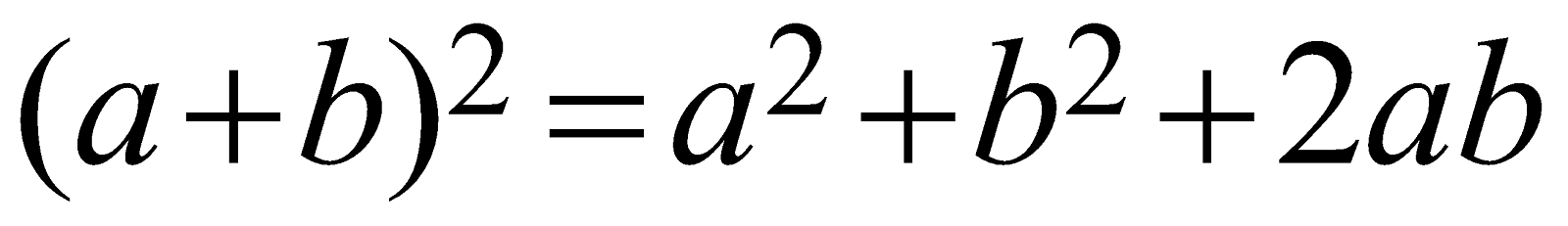 is an “algebraic identity”.
is an “algebraic identity”.
What Are The Properties of Algebraic Identities?
The following are some of the properties of algebraic identities.
An algebraic identity does not have a finite number of solutions, as it holds good for an infinite number of values that you put in place of its variables.
The algebraic identities are used in the simplification of algebraic polynomials.
The algebraic identities may be used in the factorization of algebraic expression
The algebraic identities help in solving any algebraic equation.
The algebraic identities may be conditional also. For example \[{{a}^{3}}+{{b}^{3}}+{{c}^{3}}=3abc,\quad when\ \ a+b+c=0\]
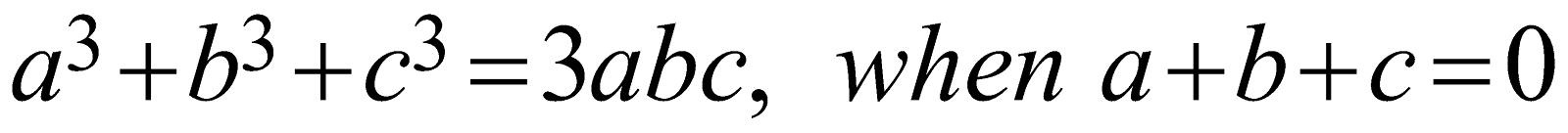
What Are Algebraic Polynomials?
Algebraic polynomials are those expressions or equations which involve only the non-negative integral power of variables of the algebraic expressions or equations but may contain any integral coefficients and constants.
Following are examples of algebraic polynomials.
\[{{(a+b)}^{3}},\ \ {{a}^{2}}+{{b}^{2}}+2ab,\ \ {{x}^{2}}+{{y}^{2}}+2\sqrt{3}\]
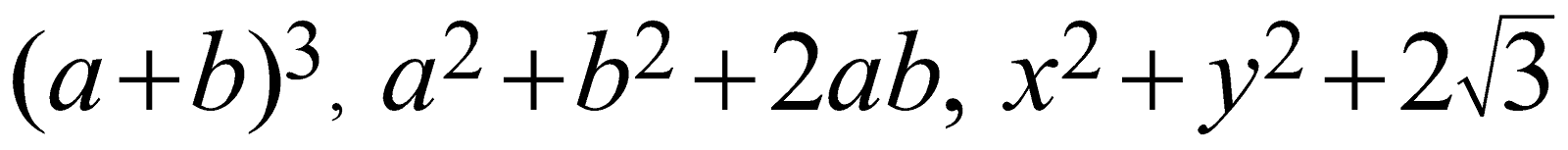
Chart Of Identities Of Factorization Of Polynomials
As you can exploit the algebraic identities both to simplify and factorize the algebraic expressions, here is a quick reference to some of the algebraic identities that you can use for factorization of polynomials.
Algebraic Identities | |
Description | Formulae |
Whole square of the sum of any two variables | \[{{(a+b)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\]
|
Whole square of the difference between any two variables. | \[{{(a-b)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\]
|
Difference between any two squares | \[{{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)\]
|
Whole square of the sum of any three variables | \[{{(a+b+c)}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ca\]
|
Whole cube of the sum of any two variables | \[{{(a+b)}^{3}}={{a}^{3}}+{{b}^{3}}+3a{{b}^{2}}+3{{a}^{2}}b\]
|
Whole cube of the difference between any two variables. | \[{{(a-b)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\]
|
Sum of any two cubes | \[{{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\]
|
Difference between any two cubes | \[{{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\]
|
Whole cube of the sum of any three variables | \[{{(a+b+c)}^{3}}={{a}^{3}}+{{b}^{3}}+{{c}^{3}}+3\left( a+b \right)\left( b+c \right)\left( c+a \right)\]
|
Chart Of Algebraic Identities
The following are some of the algebraic identities that you will find useful for simplification of algebraic terms or factorization of an algebraic expression or solving any algebraic equation.
Algebraic Identities |
\[(x+a)(x+b)={{x}^{2}}+\left( a+b \right)x+ab\]
|
\[{{a}^{2}}+{{b}^{2}}+{{c}^{2}}-ab-bc-ca=\frac{1}{2}\left[ {{\left( a-b \right)}^{2}}+{{\left( b-c \right)}^{2}}+{{\left( c-a \right)}^{2}} \right]\]
|
\[{{a}^{4}}-{{b}^{4}}=\left( {{a}^{2}}+{{b}^{2}} \right)\left( a+b \right)\left( a-b \right)\]
|
\[{{a}^{3}}+{{b}^{3}}+{{c}^{3}}-3abc=\frac{1}{2}(a+b+c)\left[ {{\left( a-b \right)}^{2}}+{{\left( b-c \right)}^{2}}+{{\left( c-a \right)}^{2}} \right]\]
|
\[{{a}^{4}}+{{a}^{2}}+1=\left( {{a}^{2}}+a+1 \right)\left( {{a}^{2}}-a+1 \right)\]
|
\\ a^3+b^3+c^3=3 a b c, when \ \ a+b+c=0 \\ a^3+b^3+c^3 \neq 3 a b c, when \ \ a+b+c \neq 0
|
\[a-b=\left( \sqrt{a}+\sqrt{b} \right)\left( \sqrt{a}-\sqrt{b} \right),\ \ for\ a,b>0\]
|
Frequently Asked Questions (FAQs)
Some of the different types of identities are
Algebraic Identities
Trigonometric Identities
Mensuration Identities
Geometric Identities
An algebraic identity is true for all the values of its variables. An algebraic equation, if solvable, has a finite number of solutions.
As such an algebraic identity cannot be solved. An algebraic identity can have an infinite number of values that you put in place of its variables. This is the essence of an algebraic identity that it is always true for any value of the variable.
The basic rules of algebraic operations, which include addition, subtraction, division multiplication are as follows:
Associative law
\begin{aligned}
& x+(y+z)=(x+y)+z \\
& x \times(y \times z)=(x \times y) \times z
\end{aligned}
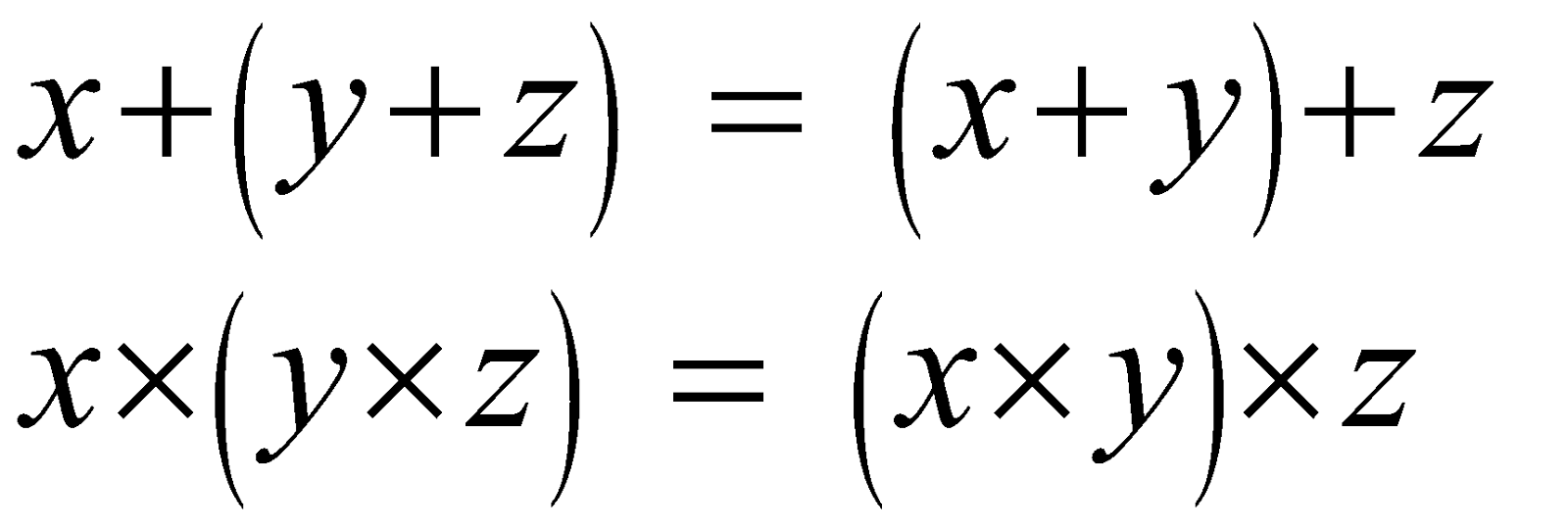
Commutativity law
\begin{aligned}
& x+y=y+x \\
& y \times z=z \times y
\end{aligned}
![]()
An algebraic expression involves variables, arithmetic operators, and constants. On the other hand, an algebraic equation is what you get on writing two algebraic expressions using the "equal to" sign or relating an algebraic expression to any constant.