a + b Whole Square - Proof | (a+b)^2 Formula

a + b Whole Square : A Plus B Whole Square Formula - Proof | (a+b)^2 Formula

Edited By Team Careers360 | Updated on Jul 02, 2025 05:15 PM IST

Mathematics is totally a game of formulas. In mathematics, solutions to most of the questions are found by using appropriate formulas. Generally, formulas for the square of sum of two numbers and the square of the difference of two numbers are used in expansion or in simplification. The formula of a plus b whole square is also one of the formulas which are mostly used in the expansion and simplification of a given expression. The whole square of a plus b means the product of a plus b with itself.

This Story also Contains

Formula Of a Plus b Whole Square
Examples Of a Plus b Whole Square
Expansion Of a – b whole Square By Using Formula of a + b Whole Square
Application Of a Plus b Whole Square In Real Life

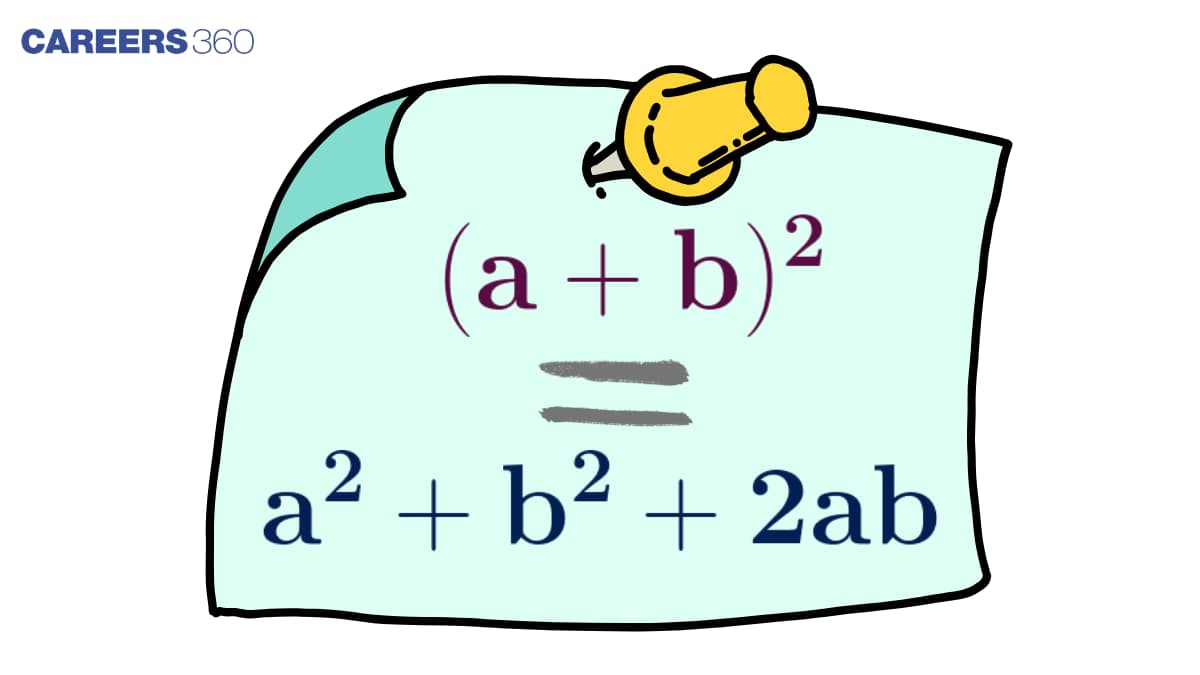
a + b Whole Square : A Plus B Whole Square Formula - Proof | (a+b)^2 Formula

Formula Of a Plus b Whole Square

In order to get the expanded form of a plus b whole square we have to multiply the a plus b with a plus b. Then by using the property or rule of algebraic multiplication we will get a + b whole square.

${(a + b)^2} = (a + b) \times (a + b)$

$(a + b) \times (a + b) = {a^2} + ab + ba + {b^2}$

${(a + b)^2} = {a^2} + 2ab + {b^2}$

Examples Of a Plus b Whole Square

Solve

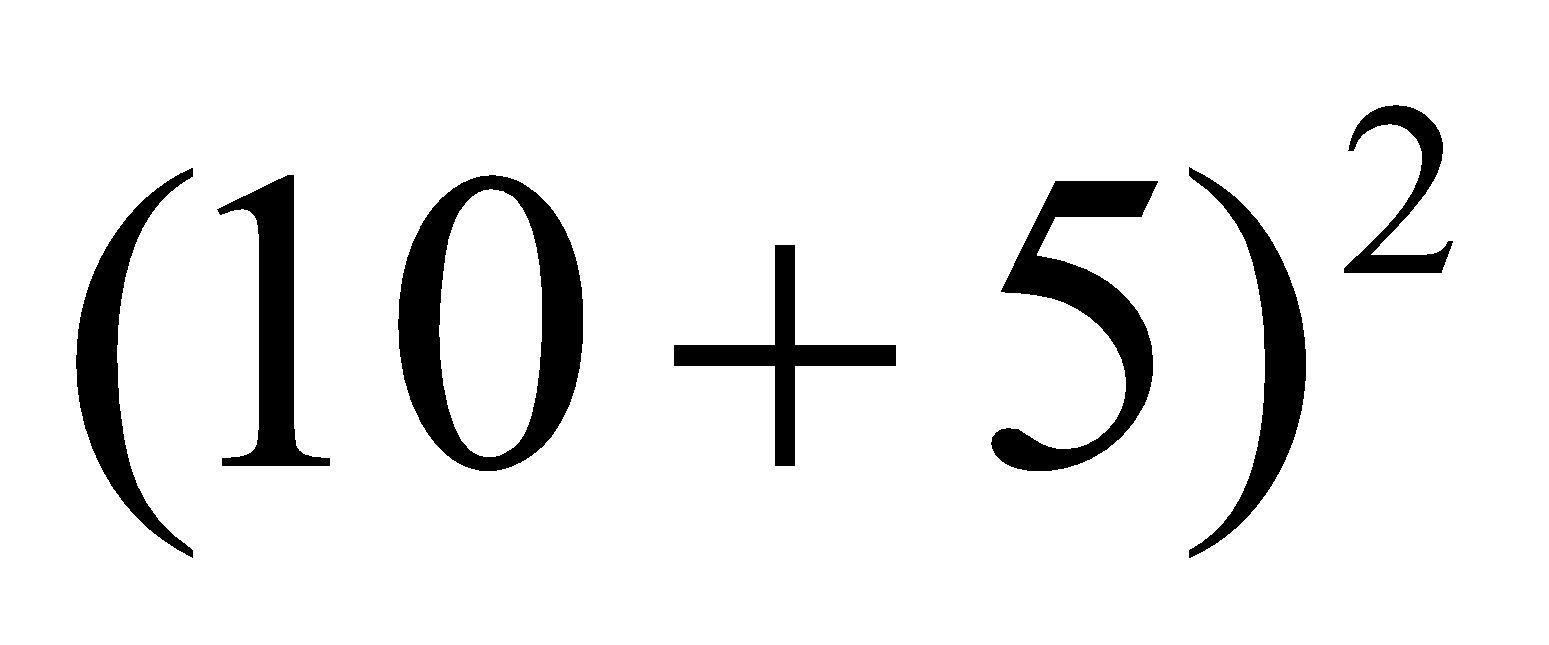
Solve ${(10 + 5)^2}$

Solution:

${(10 + 5)^2} = {10^2} + 2 \times 10 \times 5 + {5^2}$

${10^2} + 2 \times 10 \times 5 + {5^2} = 100 + 100 + 25$

${(10 + 5)^2} = 225$

Solve

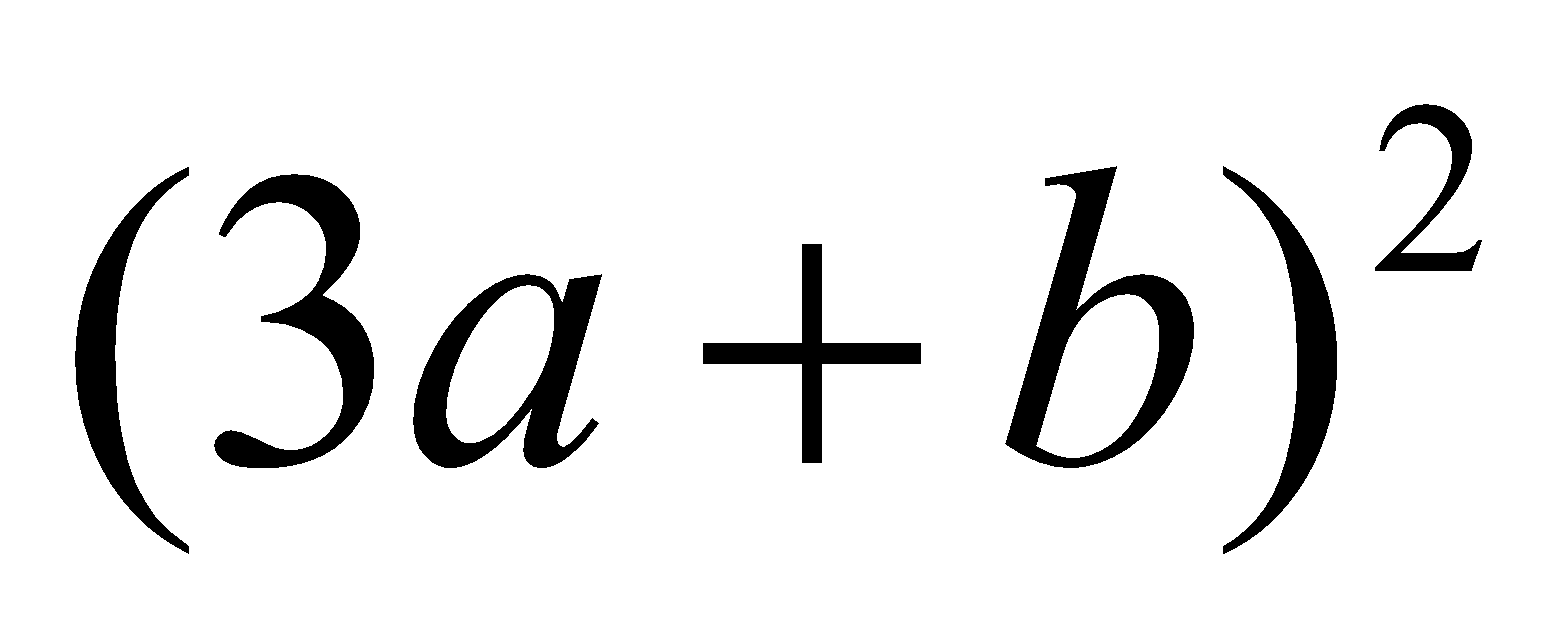
Solve ${(3a + b)^2}$

Solution:

${(3a + b)^2} = 9{a^2} + 2 \times 3a \times b + {b^2}$

${(3a + b)^2} = 9{a^2} + 6ab + {b^2}$

Expansion Of a – b whole Square By Using Formula of a + b Whole Square

In order to get expansion of a - b whole square we have to multiply the ‘a’ + (-b) with a + (-b). Then by using the property or rule of algebraic multiplication we will get a + b whole square.

${(a - b)^2} = (a + ( - b)) \times (a + ( - b))$

$(a + ( - b)) \times (a + ( - b)) = {a^2} - ab - ba + {b^2}$

${(a - b)^2} = {a^2} - 2ab + {b^2}$

Application Of a Plus b Whole Square In Real Life

In order to understand the application of a + b whole square in real life let us suppose you have to find the square of 1005 which is a large number you have two choices either you will multiply 1005 with 1005 which is time-consuming or you will use expansion form of a + b whole square which will reduce calculation as well as time.

${(1005)^2} = {(1000 + 5)^2}$

${(1000 + 5)^2} = {1000^2} + {5^2} + 2 \times 1000 \times 5$

${(1005)^2} = 1000000 + 25 + 10000$

${(1005)^2} = 1010025$

Frequently Asked Questions (FAQs)

1. What is simplification in mathematics?

Simplification is a process of reducing large expressions into simple and small expressions. In other words, it is the process of making complex equations or expressions simple.

2. Write the expanded form of a plus b whole square?

${(a + b)^2} = {a^2} + 2ab + {b^2}$

3. Write the simplest form of a square plus b square plus two ab?

${a^2} + 2ab + {b^2} = {a^2} + ab + ab + {b^2}$

${a^2} + ab + ab + {b^2} = a(a + b) + b(a + b)$

$a(a + b) + b(a + b) = (a + b)(a + b)$

$(a + b)(a + b) = {(a + b)^2}$

4. What is the meaning of the whole square?

Whole square means multiplication of the whole expression twice with itself.

5. What is the meaning of the whole cube?

Whole cube means multiplication of the whole expression thrice with itself.

6. How to find the formula of a plus b whole square?

${(a + b)^2} = (a + b) \times (a + b)$

$(a + b) \times (a + b) = {a^2} + ab + ba + {b^2}$

${(a + b)^2} = {a^2} + 2ab + {b^2}$

7. Why is the (a+b)^2 formula important in algebra?

The (a+b)^2 formula is important because it allows us to quickly expand the square of a binomial without having to multiply it out step-by-step. It's a fundamental algebraic identity used in various mathematical applications and problem-solving.

8. How does the (a+b)^2 formula relate to perfect square trinomials?

The result of the (a+b)^2 formula, a^2 + 2ab + b^2, is a perfect square trinomial. Recognizing this pattern is crucial for factoring quadratic expressions and solving certain types of equations.

9. How can the (a+b)^2 formula be used in mental math?

The formula can be used for quick mental calculations. For example, to square 52, we can think of it as (50+2)^2 = 50^2 + 2(50)(2) + 2^2 = 2500 + 200 + 4 = 2704, which is often faster than multiplying 52 by 52 directly.

10. How does understanding (a+b)^2 help in factoring quadratic expressions?

Recognizing the expanded form of (a+b)^2 helps in identifying perfect square trinomials. If a quadratic expression can be written as a^2 + 2ab + b^2, it can be factored as (a+b)^2, which is crucial in solving certain quadratic equations.

11. Can the (a+b)^2 formula be extended to more than two terms?

Yes, the concept can be extended to more terms, but the formula becomes more complex. For three terms, we have (a+b+c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ac. This is known as the square of a trinomial.

12. What's the difference between (a+b)^2 and a^2 + b^2?

(a+b)^2 equals a^2 + 2ab + b^2, while a^2 + b^2 lacks the middle term 2ab. This is a common misconception. The square of a sum is not equal to the sum of squares; it includes an additional term representing twice the product of the two quantities.

13. Why is the middle term in (a+b)^2 always positive?

The middle term 2ab is always positive because it's the product of 2 (which is positive) and ab. Even if a or b is negative, their product appears twice, ensuring the middle term is positive in the expanded form.

14. Can the (a+b)^2 formula be used with variables other than a and b?

Yes, the formula works with any two algebraic terms. For example, (x+y)^2 = x^2 + 2xy + y^2, or (2m+3n)^2 = (2m)^2 + 2(2m)(3n) + (3n)^2 = 4m^2 + 12mn + 9n^2.

15. What's the geometric interpretation of the 2ab term in the (a+b)^2 formula?

Geometrically, the 2ab term represents the area of two rectangles, each with sides a and b, in the square formed by (a+b)^2. These rectangles account for the additional area beyond just a^2 and b^2.

16. How does the (a+b)^2 formula relate to the concept of polynomial expansion?

The (a+b)^2 formula is a fundamental example of polynomial expansion. It demonstrates how terms combine and simplify when a binomial is multiplied by itself, serving as a stepping stone to understanding more complex polynomial expansions.

17. What happens if we replace 'b' with '-b' in the formula?

If we replace 'b' with '-b', we get the formula for (a-b)^2, which is a^2 - 2ab + b^2. Notice that the middle term becomes negative, while the other terms remain the same as in (a+b)^2.

18. What's the relationship between (a+b)^2 and (a-b)^2?

The formulas for (a+b)^2 and (a-b)^2 are similar, with the only difference being the sign of the middle term. (a+b)^2 = a^2 + 2ab + b^2, while (a-b)^2 = a^2 - 2ab + b^2. Their sum is always 2(a^2 + b^2).

19. How does the (a+b)^2 formula relate to the difference of squares formula?

While (a+b)^2 expands a sum of squares, the difference of squares formula, a^2 - b^2 = (a+b)(a-b), factors a difference of squares. They are different but related algebraic identities used in various mathematical contexts.

20. Can the (a+b)^2 formula be applied to complex numbers?

Yes, the formula works for complex numbers as well. If a and b are complex numbers, (a+b)^2 still equals a^2 + 2ab + b^2, where the operations are performed according to the rules of complex arithmetic.

21. How does the (a+b)^2 formula change if a and b are matrices?

For matrices, (A+B)^2 = (A+B)(A+B) = A^2 + AB + BA + B^2. Note that unlike scalar algebra, AB is not necessarily equal to BA for matrices, so we can't always simplify this to A^2 + 2AB + B^2.

22. What is the a + b whole square formula?

The a + b whole square formula, also known as (a+b)^2 formula, states that (a+b)^2 = a^2 + 2ab + b^2. This formula expresses the square of a sum as the sum of the squares of the individual terms plus twice their product.

23. How can you prove the (a+b)^2 formula algebraically?

To prove (a+b)^2 algebraically, expand (a+b)(a+b):

24. How does the geometric representation of (a+b)^2 help in understanding the formula?

The geometric representation of (a+b)^2 shows a square with side length (a+b). This square can be divided into four parts: a square of side a, a square of side b, and two rectangles each with sides a and b. This visual aids in understanding why the formula is a^2 + 2ab + b^2.

25. How does the (a+b)^2 formula relate to the FOIL method?

The (a+b)^2 formula is a special case of the FOIL (First, Outer, Inner, Last) method for multiplying binomials. When we FOIL (a+b)(a+b), we get a^2 + ab + ab + b^2, which simplifies to a^2 + 2ab + b^2, the same result as the formula.

26. What's the significance of the 2ab term in the (a+b)^2 formula?

The 2ab term represents the interaction between a and b when squaring (a+b). It accounts for the fact that we're not just squaring a and b individually, but also considering how they combine when squared together.

27. How can the (a+b)^2 formula be used to approximate square roots?

The formula can be used to approximate square roots by expressing the number as a sum of a perfect square and a small number. For example, √26 ≈ (5+0.1)^2 = 5^2 + 2(5)(0.1) + 0.1^2 = 25 + 1 + 0.01 ≈ 5.1.

28. What's the connection between the (a+b)^2 formula and the binomial theorem?

The (a+b)^2 formula is a special case of the binomial theorem when the exponent is 2. The binomial theorem generalizes this concept for any positive integer exponent, not just 2.

29. How does the (a+b)^2 formula relate to completing the square?

The (a+b)^2 formula is fundamental to the method of completing the square. When solving quadratic equations, we often aim to transform the quadratic expression into the form (x+p)^2 + q, which directly uses this formula.

30. What's the relationship between (a+b)^2 and (a+b)(a-b)?

While (a+b)^2 = a^2 + 2ab + b^2, (a+b)(a-b) = a^2 - b^2. The difference between these formulas shows why a^2 - b^2 is called the difference of squares.

31. How can the (a+b)^2 formula be used in probability and statistics?

In probability and statistics, the formula appears in the calculation of variance: Var(X+Y) = Var(X) + Var(Y) + 2Cov(X,Y). This is analogous to (a+b)^2 = a^2 + b^2 + 2ab, where Cov(X,Y) plays the role of ab.

32. Can the (a+b)^2 formula be used with fractional or irrational numbers?

Yes, the formula works with any real numbers, including fractions and irrationals. For example, (√2 + 1/3)^2 = (√2)^2 + 2(√2)(1/3) + (1/3)^2 = 2 + 2√2/3 + 1/9.

33. How does the (a+b)^2 formula relate to the concept of squared binomials in algebra?

The (a+b)^2 formula is the definition of a squared binomial in algebra. It shows how to expand any binomial that's raised to the power of 2, which is a fundamental concept in algebraic manipulation and simplification.

34. What's the connection between the (a+b)^2 formula and the concept of area in geometry?

The (a+b)^2 formula directly relates to the area of a square with side length (a+b). The terms a^2, b^2, and 2ab represent the areas of different parts of this square, providing a geometric interpretation of the algebraic formula.

35. How can understanding the (a+b)^2 formula help in solving word problems?

Understanding this formula can help in solving word problems involving areas, growth rates, or any situation where a quantity is squared. It allows for quick mental calculations and helps in setting up equations for more complex problems.

36. What's the significance of the (a+b)^2 formula in calculus?

In calculus, the (a+b)^2 formula is used in various contexts, such as in Taylor series expansions and in deriving rules for differentiation and integration. It's also crucial in understanding the behavior of quadratic functions.

37. How does the (a+b)^2 formula relate to the concept of perfect squares in algebra?

The result of the (a+b)^2 formula, a^2 + 2ab + b^2, is always a perfect square trinomial. Recognizing this pattern is crucial for identifying and factoring perfect square trinomials in more complex algebraic expressions.

38. Can the (a+b)^2 formula be extended to negative exponents?

While the formula itself doesn't directly apply to negative exponents, understanding it helps in working with expressions like 1/(a+b)^2. This can be expanded using the formula and then simplified using rules for fractions and exponents.

39. How does the (a+b)^2 formula relate to the concept of polynomial identities?

The (a+b)^2 formula is one of the basic polynomial identities, along with (a-b)^2 and (a+b)(a-b). These identities form the foundation for more complex algebraic manipulations and are crucial in simplifying and factoring polynomials.

40. What role does the (a+b)^2 formula play in understanding quadratic functions?

The formula is essential in understanding the behavior of quadratic functions. It helps in identifying the vertex form of a quadratic function, which is crucial for determining its maximum or minimum point and its overall shape.

41. How can the (a+b)^2 formula be used to understand the concept of completing the square geometrically?

Geometrically, completing the square involves adding area to a rectangle to form a perfect square. The (a+b)^2 formula shows how this additional area (represented by the 2ab term) relates to the dimensions of the original rectangle.

42. What's the relationship between the (a+b)^2 formula and the concept of algebraic expansion?

The (a+b)^2 formula is a fundamental example of algebraic expansion. It demonstrates how terms combine when a binomial is multiplied by itself, serving as a model for understanding more complex expansions.

43. How does the (a+b)^2 formula relate to the concept of algebraic factoring?

While the formula itself is an expansion, recognizing its result (a^2 + 2ab + b^2) is crucial for factoring. When encountering this pattern in a quadratic expression, it can be factored back into (a+b)^2.

44. Can the (a+b)^2 formula be applied in three-dimensional geometry?

Yes, the concept extends to three dimensions. For example, the volume of a cube with side (a+b) is (a+b)^3, which expands to a^3 + 3a^2b + 3ab^2 + b^3, following a similar pattern but with more terms.

45. How does the (a+b)^2 formula relate to the concept of algebraic proofs?

The formula serves as a simple yet powerful example of algebraic proof. Proving it through expansion demonstrates the logical steps involved in verifying algebraic identities, which is a fundamental skill in higher mathematics.

46. What's the significance of the (a+b)^2 formula in number theory?

In number theory, the formula is used in various proofs and concepts. For example, it's used in proving that the sum of two squares can also be expressed as a sum of two squares in different ways, which is important in studying Pythagorean triples.

47. How can the (a+b)^2 formula be used to understand the concept of algebraic structure?

The formula demonstrates the distributive property of multiplication over addition in algebra. It shows how the structure of algebra allows us to multiply complex expressions and combine like terms, which is fundamental to algebraic manipulation.

48. What's the connection between the (a+b)^2 formula and the concept of polynomial long division?

While not directly related, understanding the (a+b)^2 formula helps in polynomial long division. Recognizing patterns like a^2 + 2ab + b^2 can simplify the division process, especially when dealing with quadratic dividends or divisors.

49. How does the (a+b)^2 formula relate to the concept of algebraic identities in trigonometry?

The formula is analogous to trigonometric identities like sin^2(θ) + cos^2(θ) = 1. Understanding algebraic identities like (a+b)^2 prepares students for more complex identities in trigonometry and other areas of mathematics.

50. Can the (a+b)^2 formula be used in understanding concepts in linear algebra?

Yes, the formula extends to linear algebra, particularly in understanding quadratic forms. For matrices A and B, (A+B)^2 follows a similar pattern, though matrix multiplication rules must be considered.

51. How does the (a+b)^2 formula relate to the concept of algebraic symmetry?

The formula demonstrates algebraic symmetry. The terms a^2 and b^2 are symmetrical, while the middle term 2ab represents the interaction between a and b. This symmetry is preserved even when the values of a and b are