A Cube Plus B Cube Formula | a^3 + b^3 Formula
The identity a cube + b cube, often written as $a^3+ b^3$, is one of the fundamental algebraic formulas used to simplify expressions and solve equations involving cubes of binomials. It is closely related to several other key expressions, such as a cube + b cube formula, a cube - b cube, and the $(a+b)^3$ formula, all of which are essential in algebraic expansion and factorisation. Whether you're trying to find the value of a cube-b cube, understand how a cube plus b cube is equal to a factored form, or simplify a plus b whole cube, mastering these expressions helps in faster calculations and deeper conceptual clarity. In this article, we’ll explore the complete breakdown, derivation, and applications of the $a^3+b^3$ formula and its related variations in mathematics.
This Story also Contains
- What is $a^3 + b^3$?
- Derivation of $a^3 + b^3$ using algebraic expansion
- $a^3 + b^3$ in Terms of a + b and ab
- Graphical Interpretation of $a^3 + b^3$
- Application in Polynomial Factorisation
- Solved Examples based on $a^3+b^3$
- List of Topics Related to the A cube plus B cube Formula
- NCERT Resources
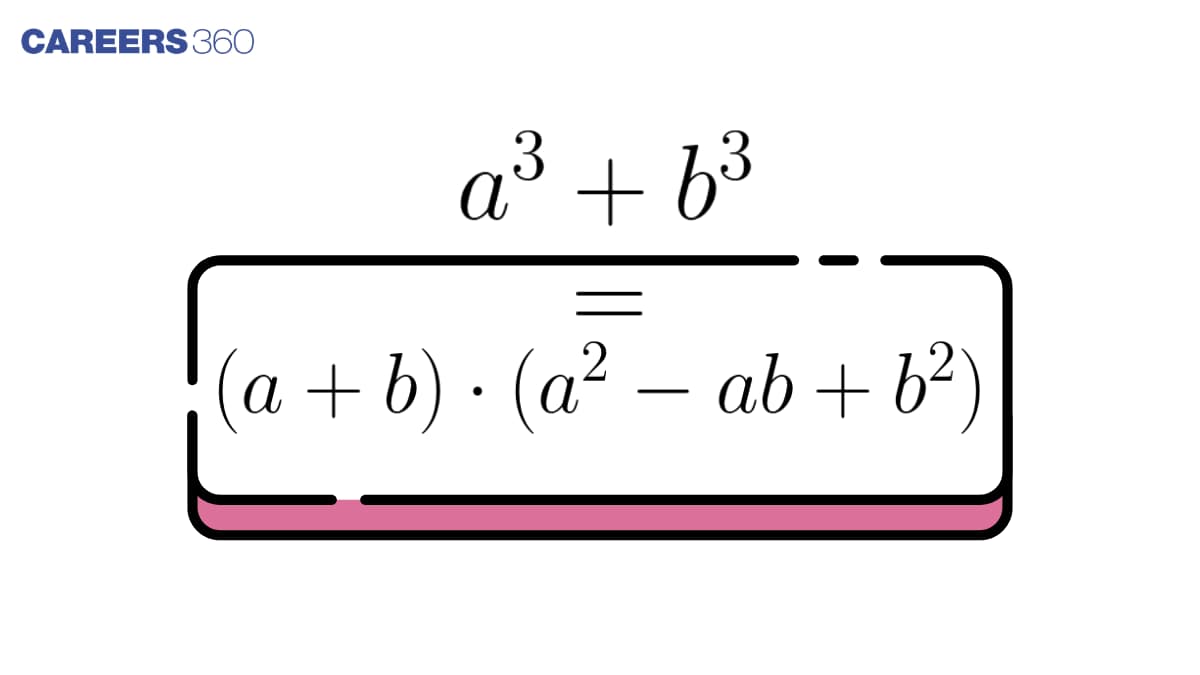
What is $a^3 + b^3$?
The expression a cube + b cube, written as $a^3 + b^3$ represents the sum of the cubes of two algebraic terms, $a$ and $b$. This algebraic identity is used to simplify cubic expressions and is commonly seen in algebraic factorisation, especially when solving for roots of cubic polynomial equations. Students often search for this identity using terms like a cube + b cube formula or a cube + b cube when learning how to break down complex cube terms into simpler factors.
Standard form of $a^3 + b^3$ formula
The standard identity for $a^3 + b^3$ is:
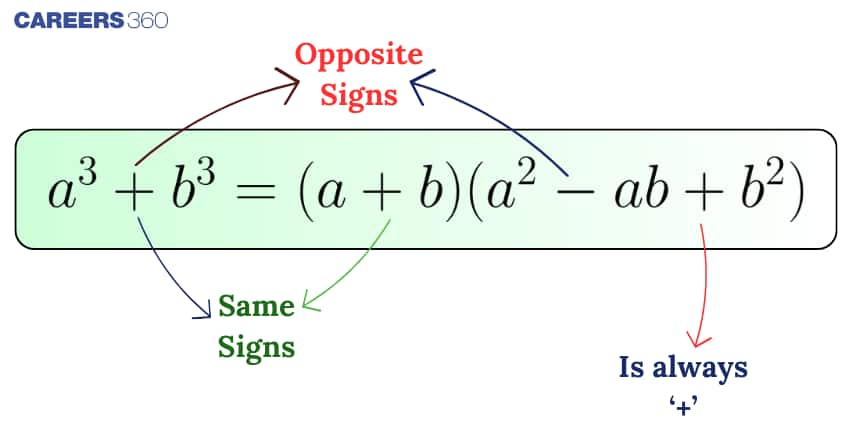
$a^3 + b^3 = (a + b)(a^2 - ab + b^2)$
This is a fundamental formula in algebra used to factor the sum of cubes. It tells us that the sum of two cubes can always be written as a product of a binomial and a trinomial. When people search for a cube + b cube is equal to or a cube + b cube formula, they are essentially referring to this key identity.
Common notations: a cube + b cube and $(a+b)^3$
It’s important not to confuse $a^3 + b^3$ (a cube + b cube) with the cube of a sum, which is written as $(a + b)^3$. The expansion of $(a + b)^3$ is:
$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$
Derivation of $a^3 + b^3$ using algebraic expansion
To derive the a cube + b cube formula, we start by assuming the standard factorised form:
$a^3 + b^3 = (a + b)(a^2 - ab + b^2)$
Let’s verify this identity using direct algebraic expansion of the right-hand side.
Start with:
$(a + b)(a^2 - ab + b^2)$
Now apply the distributive property:
$= a(a^2 - ab + b^2) + b(a^2 - ab + b^2)$
Multiply each term:
$a \cdot a^2 = a^3$
$a \cdot (-ab) = -a^2b$
$a \cdot b^2 = ab^2$
$b \cdot a^2 = a^2b$
$b \cdot (-ab) = -ab^2$
$b \cdot b^2 = b^3$
Now combine all the terms:
$a^3 - a^2b + ab^2 + a^2b - ab^2 + b^3$
Next, cancel out the like terms:
$-a^2b + a^2b = 0$
$ab^2 - ab^2 = 0$
You are left with:
$a^3 + b^3$
This confirms that:
$a^3 + b^3 = (a + b)(a^2 - ab + b^2)$
So, the a cube + b cube formula is successfully derived using algebraic expansion. This derivation helps students understand not just that a cube + b cube is equal to form, but also why it works, reinforcing their algebraic foundations. This method is particularly useful when solving factorisation problems in competitive exams or simplifying polynomial expressions.
$a^3 + b^3$ in Terms of a + b and ab
The expression $a^3 + b^3$ can also be represented in terms of simpler components like (a + b) and ab, which are often easier to work with, especially in symmetric expressions or when solving higher-order polynomial equations. This approach helps simplify algebraic calculations, making it useful in exam scenarios. Many learners search for a cube + b cube is equal to or a cube + b cube in such forms to relate the cube identity with the sum and product of variables.
Alternate representation using a + b and ab
Let us consider a scenario where you're given the values of $a + b$ and $ab$, and you're asked to find $a^3 + b^3$. In such cases, we use the identity derived from binomial expansion:
$a^3 + b^3 = (a + b)^3 - 3ab(a + b)$
This is another valid and often more practical form of the a cube + b cube formula, especially when the individual values of $a$ and $b$ are not known, but their sum and product are. It is derived from the expansion of $(a + b)^3$:
$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 = a^3 + b^3 + 3ab(a + b)$
Rearranging gives:
$a^3 + b^3 = (a + b)^3 - 3ab(a + b)$
This formula is particularly helpful when tackling MCQs or simplification problems involving symmetric expressions in a and b.
Simplifying expressions using a cube + b cube formula
By applying the $a^3 + b^3$ formula, expressions can be significantly simplified, especially when paired with substitution. For example, if you're solving a question where $a + b = 5$ and $ab = 6$, then:
$a^3 + b^3 = (a + b)^3 - 3ab(a + b)$
Substituting the values:
$= 5^3 - 3 \cdot 6 \cdot 5 = 125 - 90 = 35$
This technique makes complex expressions more manageable and is widely used in algebra, competitive exams, and even in some basic number theory problems.
Graphical Interpretation of $a^3 + b^3$
The identity $a^3 + b^3$ isn't just an abstract algebraic expression; it can also be visualised geometrically and graphically. Interpreting this expression through graphs or 3D models can deepen conceptual understanding and help connect algebra with geometry. Many students who search for a cube + b cube, a cube plus b cube is equal to, or a cube + b cube formula, may not realise that there’s a strong visual intuition behind the identity.
Understanding the Factor Form Geometrically
The factorized form: $a^3 + b^3 = (a + b)(a^2 - ab + b^2)$
Plotting $y = a^3 + b^3$ on a 3D Surface
To understand this algebraically, you can fix $a$ and $b$ as variables and consider the function:
$f(a, b) = a^3 + b^3$
This gives a 3D surface over the $a$-$b$ plane. The shape rises steeply in all directions since both $a^3$ and $b^3$ grow rapidly with positive or negative values. The function is:
Positive when both $a$ and $b$ are positive.
Negative when both $a$ and $b$ are negative.
Zero only when $a = 0$ and $b = 0$.
This helps understand how $a^3 + b^3$ behaves across different regions of the $a$-$b$ coordinate space.
Application in Polynomial Factorisation
The identity $a^3 + b^3 = (a + b)(a^2 - ab + b^2)$ plays a crucial role in simplifying and factoring cubic polynomials. When you encounter any expression of the form a cube + b cube, recognising it allows for immediate factorisation, which is especially useful in algebraic manipulation and solving higher-degree equations.
For example:
$x^3 + 8 = x^3 + 2^3 = (x + 2)(x^2 - 2x + 4)$
This kind of factorisation is essential when solving equations, finding roots, or simplifying rational expressions. Whether you’re dealing with pure algebra or calculus-based simplification, knowing the a cube + b cube formula helps break down complex terms quickly.
In exam questions, such expressions are often disguised within bigger polynomials, and recognising that a cube + b cube is equal to form becomes a time-saving strategy.
Real-life and Exam-Based Problems
While the a cube + b cube formula is most commonly used in classroom algebra, it also has practical relevance in solving real-life mathematical problems, especially those involving volume, optimisation, or design patterns.
Examples in real life:
Architecture and design: Calculating combined volumes of cubic structures.
Engineering: Determining material usage when combining cubic containers or components.
Computer science: Simplifying cubic complexity expressions in algorithm analysis.
Examples in competitive exams:
Simplifying algebraic expressions: Questions in exams like JEE, CUET, NDA, SSC, etc., frequently include expressions like $x^3 + 27$ or $a^3 + b^3$ for quick factorisation.
Solving equations: For instance, to solve $x^3 + 64 = 0$, use:
$x^3 + 4^3 = (x + 4)(x^2 - 4x + 16) = 0$ From which, you can easily find the roots.Multiple choice questions (MCQs): Identifying patterns like a cube + b cube quickly can help eliminate wrong options or spot the correct one without detailed calculations.
Mastery of the a cube + b cube formula is a vital shortcut for efficient problem-solving across a wide range of mathematical applications, both academic and real-world.
Solved Examples based on $a^3+b^3$
Example 1: Find the value of $105^3+7^3$ by using the formula of a cube plus b cube.
Solution: To find: $105^3+7^3$.
We assume that $\mathrm{a}=105$ and $\mathrm{b}=7$.
Substituting values, a cube plus b cube is equal to :
$
\begin{aligned}
& a ^3+b^ 3=(a+b)(a ^2-a b+b ^2) \\
& 105^3+7^3=(105+7)(105^2-(105)(7)+7^2) \\
& =(112)(11025-735+49) \\
& =(112)(10339) \\
& =1157968
\end{aligned}
$
Example 2: Factorise the expression $125x^3+27$ by using a cube plus b cube identity.
Solution: To factorise: $125x^3+27$.
We will use the formula for a cube plus b cube to factorise this.
We write the given expression as a cube plus b cube equals to :
$
125x^3+27=(5x)^3+3^3
$
We will substitute $a=5x$ and $b=3$ in the formula of a cube plus b cube.
$
\begin{aligned}
& a^3+b^3=(a+b)(a^2-ab+b^2) \\
& (5x)^3+3^3=(5x+3)((5x)^2-(5x)(3)+3^2) \\
& =(5x+3)(5x^2-15x+9)
\end{aligned}
$
Example 3: Simplify $29^3+30^3$ using a cube plus b cube formula.
Solution: To find $29^3+30^3$
Let us assume $\mathrm{a}=29$ and $\mathrm{b}=30$
A cube plus B cube is equal to : $a^3+b^3=(a+b)(a^2-ab+b^2)$
We substitute these in the a cube plus b cube identity.
$
\begin{aligned}
& a^3+b^3=(a+b)(a^2-ab+b^2) \\
& 29^3+30^3=(29+30)(29^2-(29)(30)+30^2) \\
& =(59)(841-870+900) \\
& =(59)(871) \\
& =51389
\end{aligned}
$
Example 4: Factor $y^3$ + 125.
Solution: $\mathrm{y}^3+125$ can be written as $\mathrm{y}^3+5^3$
Now, $\mathrm{y}^3+5^3$ is in the form of $\mathrm{a}^3+\mathrm{b}^3$.
Using the a cube plus b cube identity, $a^3+b^3=(a+b)(a^2-ab+b^2)$, we get,
$
\begin{aligned}
& y^3+5^3=(y+5)(y^2-5y+5^2) \\
& y ^3+5^3=(y+5)(y^2-5y+25)
\end{aligned}
$
Example 5: Factor the expression $27x^3+8$.
Solution: $27x^3+8$ can be written as $(3x)^3+2^3$
On comparing with the formula of a cube plus b cube, we get $\mathrm{a}^3+\mathrm{b}^3=(\mathrm{a}+\mathrm{b})(\mathrm{a}^2-\mathrm{ab}+\mathrm{b}^2)$, we have: $\mathrm{a}=3 \mathrm{x}$ and $\mathrm{b}=2$
Therefore, $(3x)^3+2^3=(3x+2)[(3x)^2-(3x) \cdot(2)+2^2]$ (using a cube plus b cube formula)
$
27x^3+8=(3x+2)[9x^2-6x+4]
$
List of Topics Related to the A cube plus B cube Formula
To fully understand and apply this identity, it’s important to explore related topics such as algebraic expressions, formulas, techniques for simplifying and evaluating, and rules for addition and subtraction of algebraic expressions. These concepts are commonly introduced through algebraic expressions worksheets and tested via targeted algebraic expressions questions.
NCERT Resources
To strengthen your understanding of the a cube plus b cube formula, refer to trusted NCERT resources. These chapters cover core concepts and identities essential for mastering algebra.
Frequently Asked Questions (FAQs)
A cube plus B cube formula, or the factors of a cube plus b cube, $a^3+b^3=(a+b)(a^2-ab+b^2)$.
A cube plus B cube plus C cube formula is given by, $a^3+b^3+c^3=(a+b+c)(a^2+b^ 2+c^2-ab-bc-ca)+$ 3abc.
A cube minus B cube is equal to $(a-b) (a^2 + ab + b^2)$.
A cube plus b cube equals to $(a + b) (a^2 - ab + b^2)$.
A cube plus B cube equals to $(a+b)(a^2-ab+b^2)$.