Algebraic Identities For Class 8
A variable is a term used in mathematics to describe a quantity that can vary or in other words change as per the expression or value. Algebraic identities are algebraic equations which is true for all values. In this article, we will cover the concept of Algebraic identities class 8 which are a set of basic identities that we are introduced in the starting of our academics to solve mathematical problems and make expressions easier to solve. We will also learn to prove these identities using distributive law and multiplication techniques.
Algebraic Identities
We define identity as an equality which is true for all values of the variable. These identities are the algebraic identities, which clearly define that the (LHS) and (RHS) of the equation is equal for all the values of the variable. Algebraic expressions are usually expressed as monomials, binomials and trinomials. This description is based on the fact that how many terms are present in the expression. It may be one, two, or three. In fact, the expression which has one or more than one terms present in it is called a polynomial and the number attached to the term is called a coefficient.
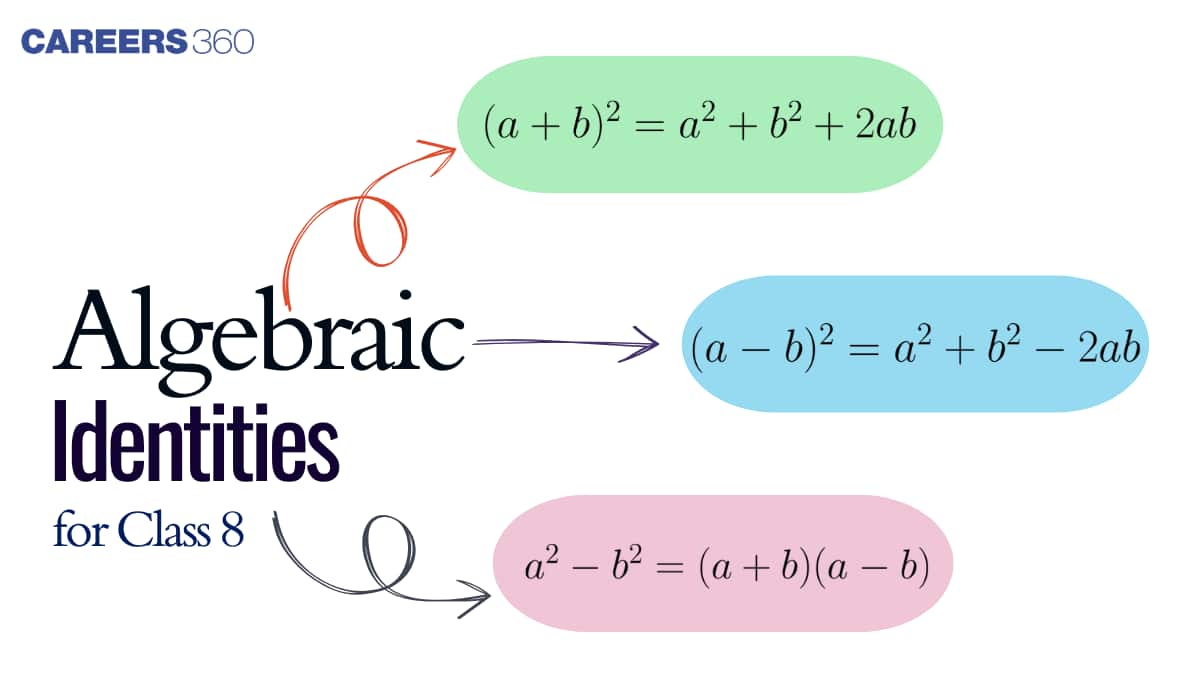
The algebraic identities class 8 consist of three major identities.
| Algebraic Identities class 8 Formulas |
| (1) $(a+b)^2=a^2+2 a b+b^2$ |
| (2) $(a-b)^2=a^2-2 a b+b^2$ |
| (3) $(a+b)(a-b)=a^2-b^2$ |
These are very basic and general algebraic identities. Substituting the values for a and b, in any of them, the left-hand side of the equation will be equal to the right-hand side. Therefore, these expressions are called as identities.
All Algebraic Identities Class 8
Identity 1: $(a + b) ^ 2 = a ^ 2 + 2ab + b ^ 2$
Proof: Lets start with left hand side,
$(a + b) ^ 2 = (a + b)(a + b)$
By distributive law;
$(a + b) ^ 2 = a(a + b) + b(a + b)$
By multiplying each term, we get,
$(a + b) ^ 2 = a ^ 2 + ab + ba + b ^ 2$
$(a + b) ^ 2 = a ^ 2 + 2ab + b ^ 2$
$L.H.S. = R.H.S.$
Identity 2: $(a - b) ^ 2 = a ^ 2 - 2ab + b ^ 2$
Proof: Lets start with left hand side,
$(a - b) ^ 2 = (a - b)(a - b)$
By distributive law;
$(a - b)² = a (a - b) - b (a - b)$
By multiplying each term, we get,
$(a - b) ^ 2 = a ^ 2 - ab - ba + b ^ 2$
$(a - b) ^ 2 = a ^ 2 - 2ab + b ^ 2$
$L.H.S. = R.H.S.$
Identity 3: $(a + b)(a - b) = a ^ 2 - b ^ 2$
Proof: Starting with left hand side, by distributive law;
$(a + b) (a - b) = a(a - b)+b(a - b)$
Multiplying each term, we get,
$(a + b)(a - b) = a ^ 2 - ab + ab - b ^ 2$
$(a + b)(a - b) = a ^ 2 - b ^ 2$
$L.H.S. = R.H.S.$
Hence, we have successfully proved all algebraic identities class 8.
Algebraic Identities Class 8 Extra Questions
Now let us look into some algebraic identities class 8 questions and answers.
Question 1: Solve $(4 x+2)(4 x-2)$ using algebraic identities.
Solution: We can write the given expression as:
$(4 x+2)(4 x-2)=(4 x)^2-(2)^2=16 x^2-4$
Question 2: Solve $(3 x+6)^2$ using algebraic identities.
Solution: We write the given expression as:
$\begin{aligned} & (3 x+6)^2=(3 x)^2+2^* 3 x^* 6+6^2 \\ & (3 x+5)^2=9 x^2+12 x+36\end{aligned}$
Question 3: Expand $(2 \mathrm{x}+2 \mathrm{y})^2$.
Solution: To expand the given expression, we substitute $a=2 x$ and $b=2 y$ in $(a+$ b) ${ }^2=a^2+2 a b+b^2$,
$
\begin{aligned}
& (2 x+2 y)^2=(2 x)^2+2(2 x)(2 y)+(2 y)^2 \\
& =4 x^2+8 x y+4 y^2
\end{aligned}
$
Question 4: Using algebraic identities for class 8, solve $296 \times 304$.
Solution: $296 × 304$ can be written as $( 300 - 4 ) \times ( 300 + 4 )$
And this is based on the algebraic identity $(a+b)(a-b)=a^2-b^2$
Here we have $a=300$, and $b=4$
Substituting the values in the above identity, we get:
$
\begin{aligned}
& (300-4)(300+4)=300^2-4^2 \\
& =90000-16 \\
& =89984
\end{aligned}
$
Question 5: Simplify $( 7x + 2y )^2 + ( 7x - 2y )^2$
Solution: To solve this, we need to use the following algebra identities:
$
\begin{aligned}
& (a+b)^2=a^2+2 a b+b^2 \\
& (a-b)^2=a^2-2 a b+b^2
\end{aligned}
$
Adding the above two formulas we have:
$
\begin{aligned}
& (a+b)^2+(a-b)^2=a^2+2 a b+b^2+a^2-2 a b+b^2 \\
& (a+b)^2+(a-b)^2=2 a^2+2 b^2
\end{aligned}
$
Here we have $\mathrm{a}=7 \mathrm{x}$ and $\mathrm{b}=2 \mathrm{y}$. Substituting this in the above expression we have:
$
\begin{aligned}
& (7 x+2 y)^2+(7 x-2 y)^2=2(7 x)^2+2(2 y)^2 \\
& =98 x^2+8 y^2
\end{aligned}
$
List of Topics Related to Algebraic Identities Class 8
Frequently Asked Questions (FAQs)
The algebraic identites class 8 are
(1) $(a+b)^2=a^2+2 a b+b^2$
(2) $(a-b)^2=a^2-2 a b+b^2$
(3) $(a+b)(a-b)=a^2-b^2$
The concepts of algebra were derived by a Persian mathematician. The birth of algebra can be credited to Babylonians.
In total, 3 such identities are there.
The algebraic identities can be easily learned through the below two simple ways:
- By visualizing the identities as square or rectangles.
- We can remember them by factored forms easily.
They have numerous applications in all diverse areas of mathematics like geometry, trigonometry, etc. These are helpful in solving problems in simple and easy way.
They are as follows:
(1) $(a+b)^2=a^2+2 a b+b^2$
(2) $(a-b)^2=a^2-2 a b+b^2$
(3) $(a+b)(a-b)=a^2-b^2$